The relativity of motion establishes the perception of an object's movement depending on the position of a reference system.
The way we perceive objects depends a lot on the position of the observer. By moving the observer, we obtain a different movement and, as a result, the analysis of this movement varies considerably.
A ball is thrown into the middle of a street. Three observers - the cat, the bird and the thrower - are positioned at different points. How does each observer perceive the movement?
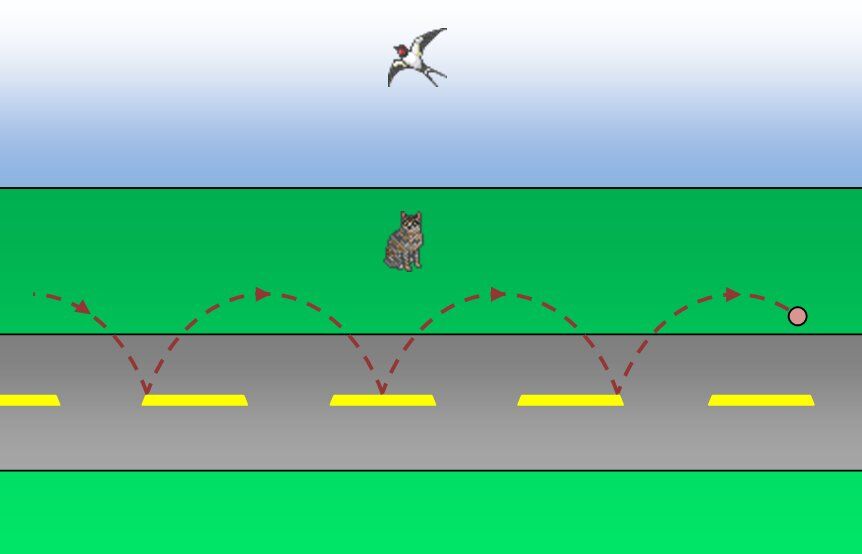
First, the cat, positioned on the side of the road, sees the ball bouncing as it moves along the road. It perceives the trajectory in this way:

As for the bird, it does not perceive the bouncing of the ball: it still sees the ball advancing down the street.

Finally, for the thrower, he sees the ball bouncing endlessly.
The three observers, placed in three different locations, described the same object; however, their perception of the movement, although accurate in each situation, was different.
The important thing to remember is that no point of view is better than another. All we need to do is choose our reference system and stick with it throughout the problem.
It is also possible to analyse the velocity of moving objects according to the position of the reference system. Since the perception of movement differs according to the position of the observer, it is possible to determine the velocity of one object relative to another.
The velocity of an object A relative to a moving object B is calculated by the formula :
|v_{A}=v_{B} + v_{AB}|
where
|v_{A}| represents the velocity of object A relative to the reference system A |\small \text {(en m/s)}|
|v_{B}| represents the velocity of body B relative to the reference system B |\small \text {(en m/s)}|
|v_{AB}| represents the velocity of reference system A relative to reference system B |\small \text {(en m/s)}|
It is therefore very important to know how to position the reference systems to accurately determine an object's velocity.
A woman is riding on a metro. She gets up and walks towards the exit door as the metro approaches its stop. Knowing that she is walking at a velocity of |\small \text {1 m/s}| compared to other stationary passengers, and that the subway is moving at |\small \text {4 m/s}|, what is the woman's velocity as perceived by an observer on the platform?
It is important to define the variables: object A represents the woman, while object B represents the metro. Thus, the velocity |v_{B}|, i.e. the speed of the metro relative to its reference system, is |\small \text {4 m/s}|. In addition, the velocity |v_{AB}|, i.e. the woman's velocity relative to the metro's reference system, is |\small \text {1 m/s}|, since she is travelling in the same direction as the metro at this velocity.
It is therefore possible to calculate the woman's velocity using the formula above.
||\begin{align} v_{A}=v_{B}+v_{AB}
\quad \Rightarrow \quad
v_{A} &= 4 \: \text {m/s} + 1 \: \text {m/s}\\
&= 5 \: \text {m/s} \end{align}||