La relativité du mouvement établit la perception du mouvement d'un objet en fonction de la position d'un système de référence.
La façon dont on perçoit les objets dépend beaucoup de la position de l'observateur. En déplaçant l'observateur, on obtient un mouvement différent et, par le fait même, l'analyse de ce mouvement varie énormément.
Une balle est lancée au milieu d'une rue. Trois observateurs, soit le chat, l'oiseau et le lanceur, sont placés à différents endroits. Quelle est la perception du mouvement pour chacun des observateurs?
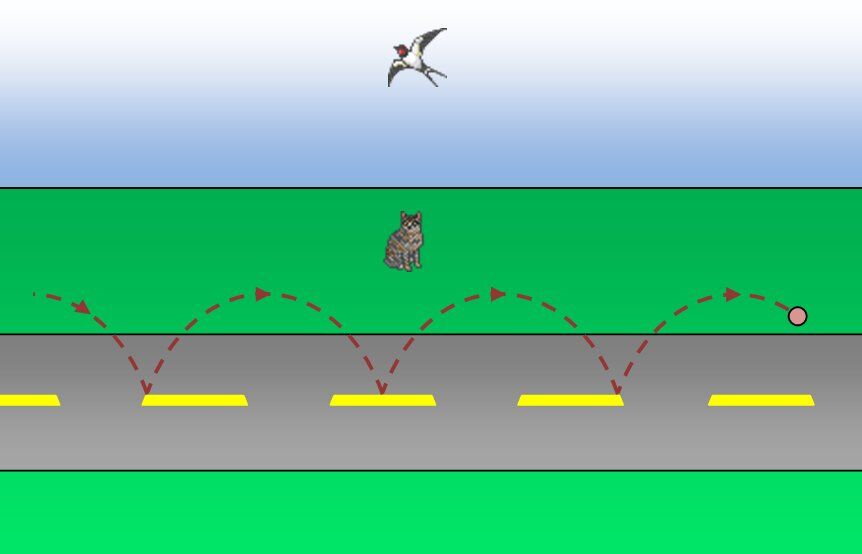
En premier lieu, le chat, positionné sur le côté de la rue, voit la balle qui rebondit tout en avançant dans la rue. Il perçoit la trajectoire ainsi:

Quant à l'oiseau, il ne perçoit pas le rebondissement de la balle: il voit quand même la balle avancer dans la rue.

Finalement, pour le lanceur, il voit la balle rebondir sans cesse.
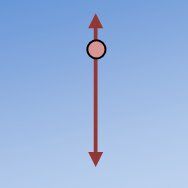
Les trois observateurs, placés à trois endroits différents, ont décrit le même objet; toutefois, leur perception du mouvement, bien qu'exacte dans chacune des situations, est différente.
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p>Ce qu'il faut retenir, c’est qu’aucun point de vue n’est meilleur qu’un autre. Il faut seulement choisir notre <a href="/fr/eleves/bv/physique/le-systeme-de-reference-p1001">système de référence</a> et le garder tout le long d'un problème.</p>
<p>Il est également possible d'analyser la vitesse des objets en mouvement selon la position du système de référence. Puisque la perception du mouvement diffère selon la position de l'observateur, il est possible de déterminer la vitesse d'un objet par rapport à un autre.</p>
</body></html>
La vitesse d'un objet A par rapport à un objet B mobile se calcule par la formule :
|v_{A}=v_{B} + v_{AB}|
où
|v_{A}| représente la vitesse de l'objet A par rapport au système de référence A |\small \text {(en m/s)}|
|v_{B}| représente la vitesse du corps B par rapport au système de référence B |\small \text {(en m/s)}|
|v_{AB}| représente la vitesse du système de référence A par rapport au système de référence B |\small \text {(en m/s)}|
Il est donc très important de savoir positionner les systèmes de référence pour déterminer avec exactitude la vitesse d'un objet.
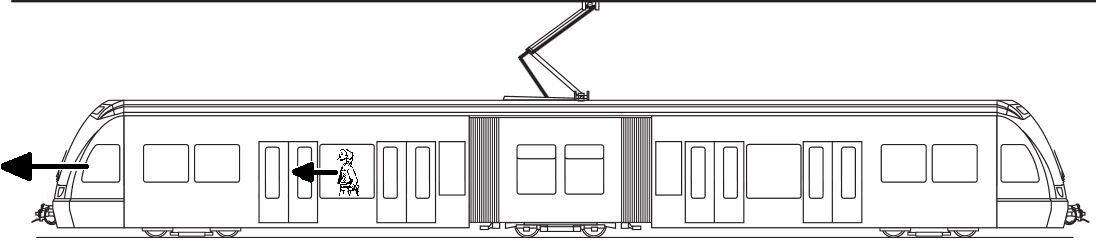
Une femme se déplace dans un métro. Elle se lève et marche vers la porte de sortie puisque le métro s'approche de son arrêt. Sachant qu'elle marche à une vitesse de |\small \text {1 m/s}| par rapport aux autres passagers immobiles, et que le métro se déplace à |\small \text {4 m/s}|, quelle est la vitesse de la femme perçue par un observateur situé sur le quai?
Il est important de définir les variables: l'objet A représente la femme, alors que l'objet B représente le métro. Ainsi, la vitesse |v_{B}|, soit la vitesse du métro par rapport à son système de référence, est de |\small \text {4 m/s}|. De plus, la vitesse |v_{AB}|, soit la vitesse de la femme par rapport au système de référence du métro, est de |\small \text {1 m/s}|, puisqu'elle se déplace dans le même sens que le métro à cette vitesse.
Il est donc possible de calculer la vitesse de la femme en utilisant la formule précédente.
||\begin{align} v_{A}=v_{B}+v_{AB}
\quad \Rightarrow \quad
v_{A} &= 4 \: \text {m/s} + 1 \: \text {m/s}\\
&= 5 \: \text {m/s} \end{align}||