The characteristics of a wave allow us to describe the wave and explain its propagation.
Regardless of the type of wave considered, they all have five characteristics in common:
The wave characteristics learned in Secondary 3 are described in detail here!
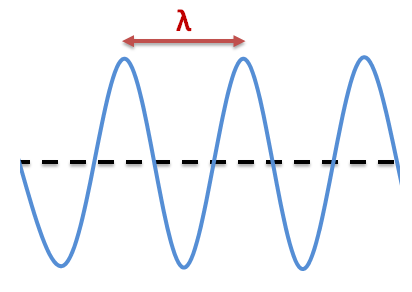
The wavelength |(\lambda)| corresponds to the length of one complete cycle of a wave.
This length corresponds to the distance that separates two identical points on the wave at a given instant separated by a complete cycle. These two points have the same amplitude. For transverse waves, the length of a complete cycle corresponds to the distance that separates two wave crests or two troughs. For a longitudinal wave, the length of the cycle is the distance between a compression zone and a rarefaction zone.
Wavelength of a transverse wave
Wavelength of a longitudinal wave

Since it's a distance, wavelength is usually measured in metres or some other unit of distance. It can also be calculated by dividing the total distance travelled by the number of cycles completed. For example, if two cycles of a wave span a length of 16 cm, we can divide this length by the number of cycles it contains, which in this case is 2. We can therefore find that the wavelength is 8 cm for one cycle.
The shorter the wavelength, the more energetic the rays. For example, X-rays have a short wavelength. Yet they emit a great deal of energy.
The frequency |\text {(f)}| is the number of cycles produced by a wave per unit of time.
The frequency of a wave can be compared to the number of people who pass a given point on a street over the course of a day. If we count that 150 people passed by this particular point, we may say that the traffic frequency is 150 people per day at this location.
To measure the frequency of a wave, count the number of cycles that form at a given point over a given period of time. This is usually done for a duration of one second. Scientists therefore established a new unit of measure that corresponds to the number of cycles per second: the hertz.
A cycle that has a duration of one second corresponds to |\text {1 Hz}.|
Wavelength and frequency are intimately linked. The shorter the wavelength, the more cycles there are per unit of time, so the higher the frequency.
For sound waves, the frequency of the wave influences the tone of the sound. The higher the frequency, the higher the tone. Conversely, a low frequency produces a low-pitched sound.
The sound that is perceptible to the human ear lies within a frequency range of between 16 Hz and 20,000 Hz. This range obviously varies from one individual to another, and decreases with age. Some animals perceive higher frequencies: dogs, for example, can perceive sounds up to 80,000 Hz and bats up to 120,000 Hz.

(Low-pitched sounds are at the top of the image, as they have the lowest frequencies; high-pitched sounds with higher frequencies are at the bottom of the image).
For light waves (the visible portion of the electromagnetic spectrum), frequency refers to the different colours emitted. The lowest frequencies (which have the longest wavelengths) correspond to the colour red, while the highest correspond to violet.
The amplitude |\text {(A)}| of a wave corresponds to the maximum height reached by the wave in relation to its resting position.
The amplitude depends on the energy transmitted by the wave. The greater the amount of energy carried by a wave, the greater the amplitude. For transverse waves, the amplitude corresponds to the maximum height of the crest or depth of the trough in relation to the equilibrium position in the middle of the wave. The amplitude of longitudinal waves is more difficult to measure, because it depends on the density of compression zones. The more compression zones there are, the greater the amplitude.
Amplitude of a transverse wave
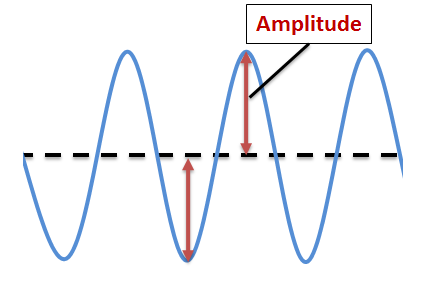
Like wavelength, amplitude is a distance, so it is measured in units derived from the metre.
Sound intensity is a function of the amplitude of the vibrations produced by the sound source. Sound amplitude is therefore a measure of the power of a sound. When the amplitude of the vibration is too small to produce a high enough intensity, a resonance box is used to amplify the sound by increasing the surface area of moving air.
The period |\text {(T)}| is the time needed for the wave to complete one full cycle.
The period is the time it takes for a wave to travel the distance of one wavelength. Since we're talking about time, we generally measure the period in seconds.
To calculate the period, we can simply time the time it takes a wave to travel the distance between two successive corresponding points. Otherwise, we can divide the total time taken by the wave to travel this distance by the number of cycles completed. For example, if two cycles of the wave take |\text {10 s}| to cover a given distance, we can say that the period of one cycle is |\text {5 s}.|
The velocity |\small \text {(v)}| corresponds to the distance traveled by a wave per unit time.
The speed of a wave can be determined mathematically if the frequency and wavelength are known.
The speed of a wave is determined by the following equation:
|v = f \times \lambda|
where
|v| represents the wave speed |\small \text {(cm/s or m/s})|
|f| represents the wave frequency |\small \text {(Hz})|
|\lambda| represents the wavelength |\small \text {(cm or m})|
What is the speed of a wave with a wavelenght of |\small \text {650 nm}| and a frequency of |\small 4.2 \times 10^{14} \text { Hz}|?
||\begin{align}
v = f \times \lambda
\quad \Rightarrow \quad
v &= 650 \times 10^{-9} \text { m} \times 4.2 \times 10^{14} \text { Hz} \\
&= 3.00 \times 10^{8} \text { m/s}
\end{align}||