Les caractéristiques d'une onde nous permettent de décrire l'onde et d'en expliquer la propagation.
Peu importe le type d'onde considéré, elles possèdent toutes cinq caractéristiques communes:
Les caractéristiques des ondes apprises en secondaire 3 sont décrites en détails ici!
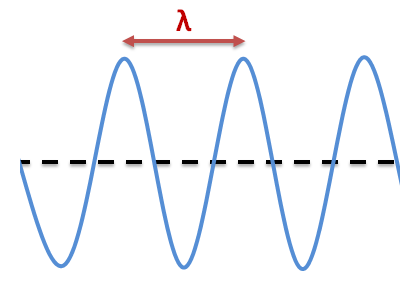
La longueur d’onde |(\lambda)| correspond à la longueur d'un cycle complet d'une onde.
Cette longueur correspond à la distance qui sépare deux points identiques de l’onde à un instant donné, séparés par un cycle complet. Les deux points sont situés à la même amplitude. Dans le cas d'une onde transversale, la longueur d'un cycle complet correspond à la distance séparant deux crêtes de l'onde ou encore deux creux. Dans le cas d'une onde longitudinale, la longueur du cycle correspond plutôt à la distance dans laquelle sont incluses une zone de compression et une zone de raréfaction.
Longueur d'onde pour une onde transversale
Longueur d'onde pour une onde longitudinale

Puisqu'il s'agit d'une distance, on la mesure généralement en mètres ou en une autre unité de distance. On peut également la calculer en divisant la distance totale parcourue par le nombre de cycles effectués. Par exemple, si deux cycles d'une onde s'étendent sur une longueur de |\small \text {16 cm}|, on peut diviser cette longueur par le nombre de cycles qu'elle contient, soit 2. On trouve donc que la longueur de cette onde est de |\small \text {8 cm}| pour un cycle.
Plus les longueurs d'onde sont petites, plus les rayons sont énergétiques. Par exemple, les rayons X ont une faible longueur d'onde. Toutefois, elles dégagent une grande quantité d'énergie.
La fréquence|\small \text {(f)}| est le nombre de cycles produits par une onde par unité de temps.
On peut comparer la fréquence d'une onde à la quantité de personnes qui circulent en un point donné d'une rue pendant une journée. Si on recense 150 personnes ayant franchi ce point précis, on peut dire que la fréquence de circulation est de 150 personnes par jour à cet endroit.
Pour mesurer la fréquence d'une onde, on dénombre le nombre de cycles qui se forment en un point donné pendant une certaine période de temps. On effectue habituellement cette mesure pour une durée d'une seconde. Les scientifiques ont donc établi une nouvelle unité de mesure correspond à la quantité de cycle par seconde, soit le hertz |\small \text {(Hz)}|.
Un cycle qui se déroule en une seconde correspond à |\small \text {1 Hz}|.
La longueur d'onde et la fréquence sont intimement liées. Plus courte est la longueur d'onde, plus il y a de cycles par unité de temps, donc plus la fréquence est grande.
Dans le cas d'une onde sonore, la fréquence de l'onde influence la tonalité du son. En effet, plus la fréquence est élevée, plus le son entendu sera aigu. À l'inverse, une basse fréquence représente un son grave.
Le son perceptible par l'oreille humaine est dans un intervalle de fréquence compris entre |\small \text {16 Hz}| et |\small \text {20 000 Hz}|. Cet écart varie évidemment selon les individus, et il diminue avec l'âge. Certains animaux perçoivent des fréquences plus élevées, par exemple le chien perçoit des sons allant jusqu'à |\small \text {80 000 Hz}| et la chauve-souris jusqu'à |\small \text {120 000 Hz}|.
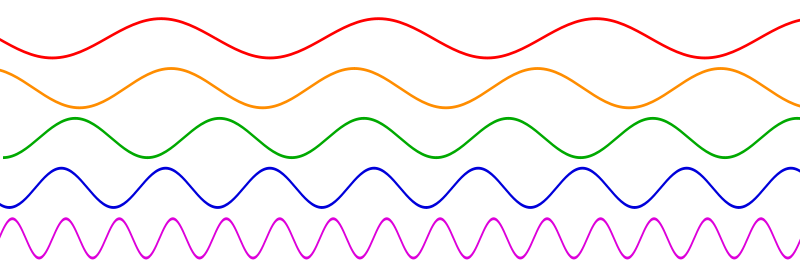
(Les sons graves sont au haut de l'image, car ils possèdent les fréquences les plus basses; les sons aigus ayant des fréquences plus élevées sont au bas de l'image).
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p>Dans le cas des ondes lumineuses (la portion visible du <a href="/fr/eleves/bv/sciences/le-spectre-electromagnetique-s1137">spectre électromagnétique</a>), la fréquence fera référence aux différentes couleurs émises. Les fréquences les plus basses (donc les longueurs d'onde les plus grandes) correspondent au rouge alors que les plus hautes correspondent au violet.</p>
</body></html>
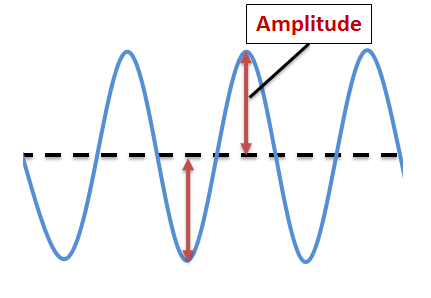
L'amplitude |\small \text {(A)}|d'une onde correspond à la hauteur maximale atteinte par l'onde par rapport à sa position au repos.
L'amplitude dépend de l'énergie transmise par l'onde. Plus la quantité d'énergie transportée par une onde est importante, plus l'amplitude est grande. Dans le cas d'une onde transversale, l'amplitude correspond à la hauteur maximale de la crête ou de la profondeur du creux par rapport à la position d'équilibre située au milieu de l'onde. Pour une onde longitudinale, l'amplitude est plus difficile à mesurer puisqu'elle est fonction de la densité des zones de compression. Plus les zones de compression comprennent de cycles, plus l'amplitude est grande.
Amplitude pour une onde transversale
Tout comme la longueur d'onde, on mesure l'amplitude en unités dérivées du mètre étant donné qu'il s'agit d'une distance.
L’intensité du son est fonction de l’amplitude des vibrations produites par la source sonore. L'amplitude sonore est donc une mesure de la puissance d'un son. Lorsque l’amplitude de la vibration est trop petite pour produire une intensité assez grande, l'utilisation d'une caisse de résonance permet d'amplifier le son en augmentant la surface d’air en mouvement.
La période |\small \text {(T)}| est le temps nécessaire à l'onde pour effectuer un cycle complet.
On peut dire que la période est le temps dont une onde a besoin pour parcourir la distance d'une longueur d'onde. Puisqu'il s'agit d'un temps, on mesure généralement la période en seconde.
Afin de calculer la période, on peut simplement chronométrer le temps que met une onde à parcourir la distance qui sépare deux points identiques successifs. On peut aussi diviser le temps total que prend l'onde pour parcourir cette distance par le nombre de cycles effectués. Par exemple, si deux cycles de l'onde prennent |\small \text {10 s}| à parcourir une distance précise, on peut dire que la période d'un cycle est de |\small \text {5 s}|.
La vitesse |\small \text {(v)}| correspond à la distance parcourue par une onde par unité de temps.
Il est possible de déterminer mathématiquement la vitesse d'une onde si la fréquence et la longueur d'onde sont connues.
La vitesse d'une onde est déterminée par l'équation suivante:
|v = f \times \lambda|
où
|v| représente la vitesse de l'onde |\small \text {(cm/s ou m/s})|
|f| représente la fréquence de l'onde |\small \text {(Hz})|
|\lambda| représente la longueur d'onde |\small \text {(cm ou m})|
Quelle est la vitesse d'une onde dont la longueur d'onde est |\small \text {650 nm}| et dont la fréquence est |\small 4,2 \times 10^{14} \small \text { Hz}|?
||\begin{align}
v = f \times \lambda
\quad \Rightarrow \quad
v &= 650 \times 10^{-9} \text { m} \times 4,2 \times 10^{14} \text { Hz} \\
&= 3,00 \times 10^{8} \text { m/s}
\end{align}||