Density, whose symbol is |\rho| (rho), is a characteristic property, which represents the quantity of matter (mass) in a given space (volume).
Mass and volume are not characteristic properties. However, the ratio between the mass and the volume of a substance, called density, is specific to each substance and allows it to be identified.
The formula used to calculate density is as follows:
|\rho= \dfrac {m}{V}|
where
|\rho| represents density |\text {(g/mL or g/cm}^3)|
|m| represents mass |\text {(g)}|
|V| represents volume |\text {(mL or cm}^3)|
The choice of units to express density depends on the state of the solution to analyze. If the substance is in a liquid state, density is calculated in grams per milliliter |\text{(g/mL})| whereas if the substance is in the solid state, density is calculated in grams per cubic centimeter |\text{(g/cm}^3)| . If the substance is in the gaseous state, density is calculated in grams per milliliter |\text{(g/mL})| or in grams per cubic centimeter
Density should not be confused with the concept of relative density (or specific gravity). Relative density is a ratio between the density of a substance and a reference density, which is water (for liquids and solids) and air (for gases). Relative density is not expressed in any particular units since it is a ratio.
Density varies according to the temperature and pressure at which a measurement is made. We must, therefore, find the density of a substance at a certain temperature and pressure if we want to be able to identify this substance.
Calculating the density of a liquid is done by dividing the measurement of its mass |\text {(g)}| by that of its volume |\text {(mL)}|.
We measure the mass of an unknown liquid using a balance (ex: triple-beam balance scale or electronic balance) to obtain a mass of |\text {25.2 g}|. Then, we measure the volume of the liquid using a graduated cylinder, obtaining a volume of |\text {18 mL}|. What is the density of this liquid?
Now, simply establish the relationship between mass and volume using the formula below:
||\begin{align} \rho =\frac{m}{V} \quad \Rightarrow \quad \rho&=\frac {\text {25.2 g}}{\text{18 mL}} \\ &= \text {1.4 g/mL} \end{align}||
Next, compare this value with the density values in the table below. The unknown liquid is corn syrup. This is because its density is the closest to the one already calculated:
||\text{1.38 g/ml} \approx \text{1.40 g/ml}||.
Here is a table that shows the density of some liquids.
| Liquid (at 20 oC) | Density (g/mL) |
|---|---|
| Gasoline | 0.750 |
| Turpentine | 0.865 |
| Olive oil | 0.920 |
| Pure water | 1.00 |
| Sea water | 1.03 |
| Glycerine | 1.26 |
| Corn syrup | 1.38 |
| Mercury | 13.6 |
To see the density of other liquids, refer to the Reference sheet - density.
Calculating the density of a solid is done by dividing the measure of its mass | \text {(g)}| by that of its volume |\text {(cm}^3)|.
What is the mass of a gold bar that has a volume of |\text {500 cm}^3|?
In the table below, the density of gold is |\text {19.3 g/cm}^3|.
The density formula is applied by replacing the variables with the known values.
|\begin{align} V&=\text {500 cm}^3 &\rho &= \text {19.3 g/cm}^3 \end{align}|
|\begin{align} \displaystyle \rho =\frac{m}{V} \quad \Rightarrow \quad
\displaystyle {m}&=\rho \times V\\
&= \text {19.3 g/cm}^3 \times \text {500 cm}^3\\
&= \text {9 650 g} \end{align}|
The mass of the gold bar is |\text {9 650 g}|.
Here is a table that shows the density of some solids.
| Solid | Density (g/cm3) |
|---|---|
| Balsa | 0.120 |
| Cork | 0.240 |
| Ice | 0.927 |
| Polyvinyl chloride (PVC) | 1.17 |
| Aluminium | 2.7 |
| Silver | 10.5 |
| Lead | 11.3 |
| Gold | 19.3 |
To see the density of other solids, refer to the Reference sheet - density.
As with liquids and solids, it is possible to calculate the density of a gas by dividing the measurement of its mass |\text {(g)}| by that of its volume |\text {(cm}^3)| or |\text {(mL)}|.
In a laboratory, hydrogen gas is collected|(H_2)| in a test tube. The volume indicated by the test tube is |\text{12 mL}| .
Knowing that |\text {1 mL = 1 cm}^3|, what is the mass of gas in the test tube?
The density formula is applied by replacing the variables with the known values.
|\begin{align} \rho &= 8.4 \times 10^{-5}\ \text{g/cm}^3 &
V&= \text{12 mL = 12 cm}^3\\
m &= ? \end{align}|
|\begin{align} \displaystyle \rho =\frac{m}{V} \quad \Rightarrow \quad
\displaystyle {m}&=\rho \times V\\
&= 8{.}4 \times 10^{-5}\text { g/cm}^3 \times \text {12 cm}^3\\
&= \text {0.001008 g}= \text {1.008 mg} \end{align}|
The mass of gas present in the test tube is |\text {1.008 mg}|.
Here is a table showing the density of some gases.
| Gaz (at 0 oC and 101.3 kPa) | Density (g/cm3) |
|---|---|
| Hydrogen (H2) | 8.99 × 10-5 |
| Helium (He) | 1.79 × 10-4 |
| Nitrogen (N2) | 1.25 × 10-3 |
| Air | 1.29 × 10-3 |
| Oxygen (O2) | 1.43 × 10-3 |
| Carbon dioxide (CO2) | 1.98 × 10-3 |
To see the density of other gases, refer to the Reference sheet - density.
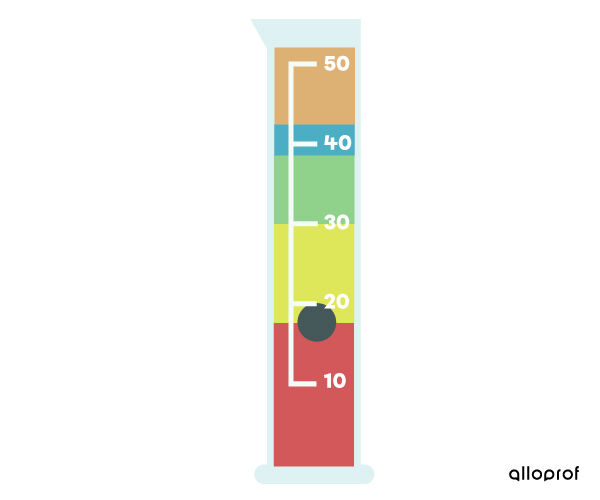
To find the layering order of different substances, use their density. The greater the density of a substance, the more it will tend to sink to the bottom of a container. On the other hand, the lower the density of a substance, the more it will tend to float on top of other denser substances.
For example, in the following graduated cylinder, the red liquid substance is the one with the highest density, while the orange liquid substance is the one with the lowest density.
In addition, the black solid substance floats on the red liquid. The density of the black solid is, therefore, lower than that of the red liquid and greater than that of the liquids above.
Pour valider ta compréhension à propos de la masse volumique de façon interactive, consulte la MiniRécup suivante :
