La masse volumique, dont le symbole est |\rho| (rhô), est une propriété caractéristique qui représente la quantité de matière
La masse et le volume ne sont pas des propriétés caractéristiques. Toutefois, le rapport entre la masse et le volume d'une substance, soit la masse volumique, est spécifique à chaque substance et permet de l'identifier.
La formule utilisée pour calculer la masse volumique est la suivante :
|\rho=\displaystyle \frac {m}{V}|
où
|\rho| représente la masse volumique |\text {(g/mL ou g/cm}^3)|
|m| représente la masse |\text {(g)}|
|V| représente le volume |\text {(mL ou cm}^3)|
Le choix des unités pour exprimer la masse volumique dépend de l’état de la solution à analyser. Si la substance est à l’état liquide, la masse volumique est calculée en grammes par millilitre |\text{(g/mL})| alors que si la substance est à l’état solide, la masse volumique est calculée en grammes par centimètre cube |\text {(g/cm}^3)|. Si la substance est à l’état gazeux, la masse volumique est calculée en grammes par millilitre |\text{(g/mL})| ou en grammes par centimètre cube |\text {(g/cm}^3)|.
Certaines techniques de laboratoire sont nécessaires au calcul de la masse volumique. Pour en savoir plus sur ces techniques, consulte ces fiches :
Il ne faut pas confondre la masse volumique avec la notion de densité. Cette dernière est un rapport entre la masse volumique d’une substance et la masse volumique de référence, soit l’eau (pour les liquides et les solides) et l’air (pour les gaz). La densité ne s’exprime pas en unités puisqu’il s’agit d’un rapport.
La masse volumique varie selon la température et la pression auxquelles une mesure est effectuée. On doit donc déterminer la masse volumique d'une substance à une certaine température et à une certaine pression si on veut pouvoir identifier cette substance.
On calcule la masse volumique d’un liquide en divisant la mesure de sa masse |\text {(g)}| par celle de son volume |\text {(mL)}|.
On mesure la masse d’un liquide inconnu à l’aide d’une balance et on obtient une masse de |\text {25,2 g}|. Ensuite, on mesure le volume du liquide à l’aide d’un cylindre gradué et on obtient un volume de |\text {18 mL}|. Quelle est la masse volumique de ce liquide?
Il suffit de faire le rapport entre la masse et le volume.
||\begin{align} \rho =\frac{m}{V} \quad \Rightarrow \quad \rho&=\frac {\text {25,2 g}}{\text{18 mL}} \\ &= \text {1,4 g/mL} \end{align}||
Ensuite, on compare cette valeur avec les valeurs de masse volumique du tableau ci-dessous. Le liquide inconnu est du sirop de maïs. En effet, sa masse volumique est la plus proche de celle calculée, car ||\text{1,38 g/ml} \approx \text{1,40 g/ml}||.
Voici un tableau qui présente la masse volumique de quelques liquides.
| Liquide (à 20 oC) | Masse volumique (g/mL) |
|---|---|
| Essence | 0,750 |
| Térébenthine | 0,865 |
| Huile d’olive | 0,920 |
| Eau douce | 1,00 |
| Eau de mer | 1,03 |
| Glycérine | 1,26 |
| Sirop de maïs | 1,38 |
| Mercure | 13,6 |
Pour avoir accès à la masse volumique d’autres liquides, consulte le Vadémécum - masse volumique.
On calcule la masse volumique d’un solide en divisant la mesure de sa masse | \text {(g)}| par celle de son volume |\text {(cm}^3)|.
Quelle est la masse d’un lingot d’or qui a un volume de |\text {500 cm}^3|?
Dans le tableau ci-dessous, la masse volumique de l’or est de |\text {19,3 g/cm}^3|.
On applique la formule de la masse volumique en remplaçant les variables par les données connues.
|\begin{align} V&=\text {500 cm}^3 &\rho &= \text {19,3 g/cm}^3 \end{align}|
|\begin{align} \displaystyle \rho =\frac{m}{V} \quad \Rightarrow \quad
\displaystyle {m}&=\rho \times V\\
&= \text {19,3 g/cm}^3 \times \text {500 cm}^3\\
&= \text {9 650 g} \end{align}|
La masse de l’or est de |\text {9 650 g}|.
Voici un tableau qui présente la masse volumique de quelques solides.
| Solide | Masse volumique (g/cm3) |
|---|---|
| Balsa | 0,120 |
| Liège | 0,240 |
| Glace | 0,927 |
| Polychlorure de vynyle (PVC) | 1,17 |
| Aluminium | 2,7 |
| Argent | 10,5 |
| Plomb | 11,3 |
| Or | 19,3 |
Pour avoir accès à la masse volumique d’autres solides, consulte le Vadémécum - masse volumique.
Tout comme pour les liquides et les solides, il est possible de calculer la masse volumique d’un gaz en divisant la mesure de sa masse |\text {(g)}| par celle de son volume |\text {(cm}^3)| ou |\text {(mL)}|.
Lors d’un laboratoire, on recueille de l’hydrogène |(H_2)| dans une éprouvette. Le volume indiqué par l’éprouvette est |\text{12 mL}|.
En sachant que |\text {1 mL = 1 cm}^3|, quelle est la masse du gaz présent dans l’éprouvette?
On applique la formule de la masse volumique en remplaçant les variables par les données connues.
|\begin{align} \rho &= 8,4 \times 10^{-5}\ \text{g/cm}^3 &
V&= \text{12 mL = 12 cm}^3\\
m &= ? \end{align}|
|\begin{align} \displaystyle \rho =\frac{m}{V} \quad \Rightarrow \quad
\displaystyle {m}&=\rho \times V\\
&= 8{,}4 \times 10^{-5}\text { g/cm}^3 \times \text {12 cm}^3\\
&= \text {0,001008 g}= \text {1,008 mg} \end{align}|
La masse de gaz présent dans l’éprouvette est de |\text {1,008 mg}|.
Voici un tableau qui présente la masse volumique de quelques gaz.
| Gaz (à 0 oC et 101,3 kPa) | Masse volumique (g/cm3) |
|---|---|
| Hydrogène (H2) | 8,99 × 10-5 |
| Hélium (He) | 1,79 × 10-4 |
| Azote (N2) | 1,25 × 10-3 |
| Air | 1,29 × 10-3 |
| Oxygène (O2) | 1,43 × 10-3 |
| Dioxyde de carbone (CO2) | 1,98 × 10-3 |
Pour avoir accès à la masse volumique d’autres gaz, consulte le Vadémécum - masse volumique.
Pour déterminer l’ordre de superposition de différentes substances, on peut utiliser leur masse volumique. Plus une substance possède une grande masse volumique, plus elle aura tendance à couler dans le fond d’un récipient. Au contraire, plus une substance possède une petite masse volumique, plus elle aura tendance à flotter sur les autres substances.
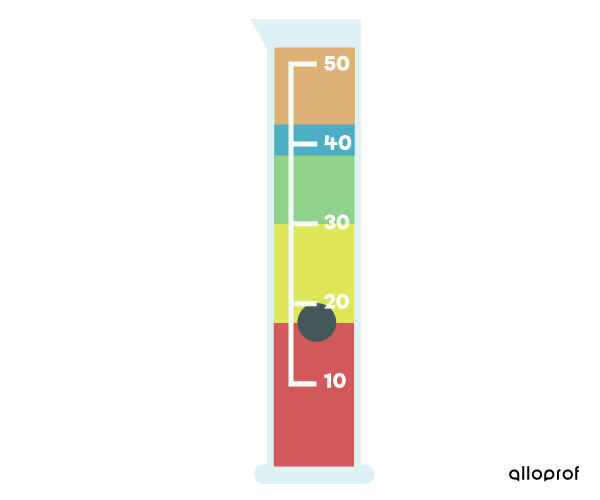
Par exemple, dans le cylindre gradué suivant, la substance liquide rouge est celle qui possède la plus grande masse volumique alors que la substance liquide orange est celle qui possède la plus petite masse volumique.
De plus, la substance solide noire flotte sur le liquide rouge. La masse volumique de la substance solide noire est donc plus petite que celle du liquide rouge et plus grande que celle des liquides plus haut.
Pour valider ta compréhension à propos de la masse volumique de façon interactive, consulte la MiniRécup suivante :
