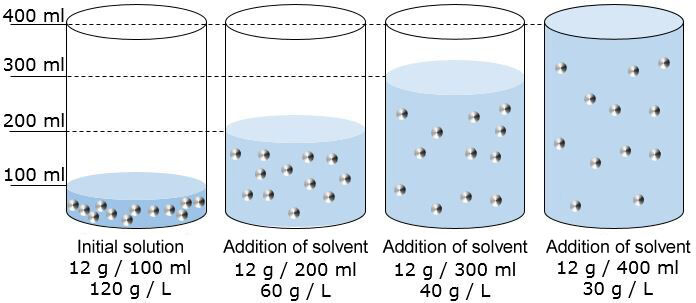
Dilution is a process used to decrease the concentration of a solution by adding solvent to it without changing the amount of solute.
Effectively, if the amount of solvent increases and the amount of solute remains the same, the volume of the total solution increases while its concentration decreases.
To make a salt water solution half as concentrated as the initial solution, double the quantity of the solution by adding solvent.
To decrease the concentration further, the principle is the same. By tripling the amount of solvent, the concentration obtained will be three times smaller than the initial solution. To obtain a solution four times lower than the initial one, the volume of the solution must be four times higher.
During a dilution, the amount of solute never changes. In other words, the mass of solute at the start is the same as after the dilution.
|m_{1} = m_{2}|
It is possible to isolate the mass by using the concentration formula.
|\displaystyle C=\frac{m}{V}\Rightarrow m=C\cdot V|
Through substitution, a formula is obtained, which establishes the relationship between the concentrations and the initial and final volumes.
|C_{1}\cdot V_{1} = C_{2} \cdot V_{2}|
where
|C_{1}| represents the concentration of the initial solution,
|V_{1}| represents the volume of the initial solution
|C_{2}| represents the concentration of the final solution
|V_{2}| represents the volume of the final solution
When using this equation, it is important that the concentrations of the initial and final solution are expressed using the same units. The same applies for volumes.
|\text {200 mL}| of sugar water solution with a concentration of |\text {20 g/L}| has been prepared. To prepare, through dilution, |\text {50 mL}| of a solution where the concentration is |\text {10 g/L}|, how much liquid must be taken from the first solution to make the solution of |\text {50 mL}|?
Here is the known data in the problem.
||\begin{align}
C_{1} &= \text {20 g/L} &V_{1} &= \text {?} \\
C_{2} &= \text {10 g/L} &V_{2} &= \text {50 mL} \\
\end{align}||
By using the dilution formula, it is possible to determine the amount to be withdrawn from the |\text {200 mL}| of the initial solution.
||\begin{align}
C_{1}\cdot V_{1} = C_{2} \cdot V_{2} \quad \Rightarrow \quad V_{1} &= \frac {C_{2} \cdot V_{2}}{C_{1}} \\
&= \frac {\text {10 g/L} \cdot \text {50 mL}}{\text {20 g/L}} \\ &= \text {25 mL}
\end{align}||
Therefore, it takes |\text {25 mL}| of the initial sugar solution to which |\text {25 mL}| of water is added to arrive at a final volume of |\text {50 mL}| and at a concentration of |\text {10 g/L}|.
What will happen to the concentration of a solution if the volume is increased tenfold (making the volume ten times greater)?
Algebraic variables will be needed to determine the effect on the final concentration.
||\begin{align}
C_{1} &= C_{1} &V_{1} &= V_{1} \\
C_{2} &= \text {?} &V_{2} &= 10 \times V_1 \\
\end{align}||
By using the dilution formula, it is possible to determine the effect on the final concentration.
||\begin{align*}
C_{1}\cdot V_{1} = C_{2} \cdot V_{2} \quad \Rightarrow \quad C_{2} &= \frac {C_{1} \cdot V_{1}}{V_{2}} \\
&= \frac {C_{1} \cdot \enclose {updiagonalstrike}[mathcolor="red"]{\color{black}{V_{1}}}}{10 \cdot \enclose {updiagonalstrike}[mathcolor="red"]{\color{black}{V_{1}}}} \\ &= \frac {C_{1}}{10}
\end{align*}||
The final concentration will be ten times smaller than the initial concentration.