The Doppler effect is a physical phenomenon whereby the frequency of a wave is modified from the point of view of the observer of the wave when the source emitting the wave and/or the observer are in relative motion to each other.
The distortion of a wave can affect a mechanical wave, such as sound, or an electromagnetic wave, such as visible light.
When an ambulance approaches a pedestrian, the pedestrian hears that the sound of the ambulance is higher in pitch than when the ambulance is stationary. When the ambulance moves away from the pedestrian, the pedestrian hears that the sound of the ambulance becomes lower in pitch.
In these cases, the tone of the sound heard by the pedestrian will be different from the actual tone of the sound emitted by the ambulance.

BlurAZ, Shutterstock.com

Sripfoto, Shutterstock.com
In the case of sound waves, the Doppler effect is quantified differently depending on the motion of the observer and the motion of the sound source. If the observer is standing still, this is what they hear.
When the ambulance (source of the sound) and the observer are at rest, the sound waves emitted by the ambulance is not affected. The wavelength |(\lambda)| oh the haerd sound is then the same as the wavelength emitted by the ambulance.
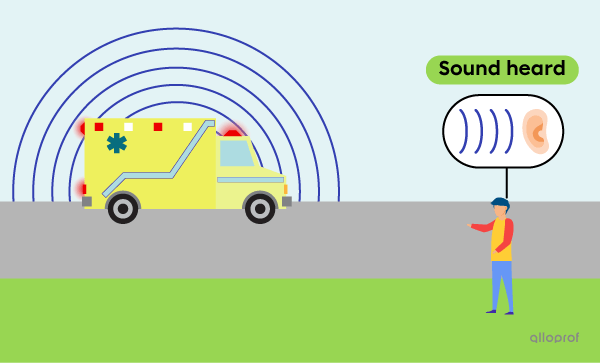
From the point of view of the observer at rest, as the ambulance moves towards him, the waves emitted contract. This means that for the observer, the wavelength is shorter and the frequency is higher. The sound is more high-pitched.
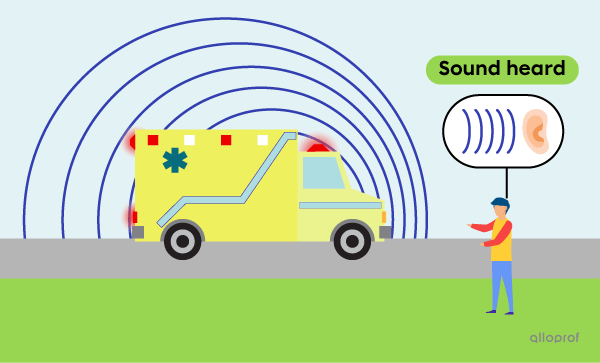
From the point of view of the observer at rest, as the ambulance moves away from him, the waves emitted strecht out. This means that for the observer, the wavelength is longer and the frequency is lower. The sound is therefore deeper lower in pitch.
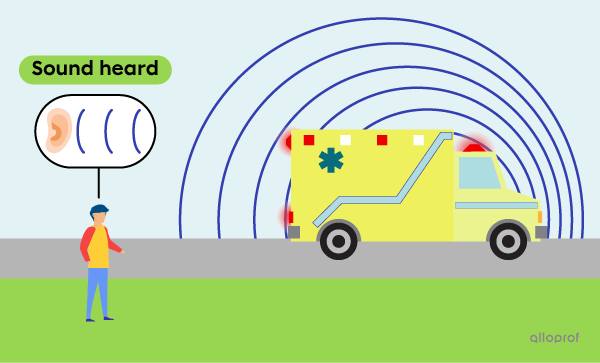
The Doppler effect is a question of reference system. From the point of view of the ambulance driver in the vehicle, the sound heard is the same as the sound emitted because he is moving at the same speed as the source of the emission, i.e. the vehicle. In other words, since the ambulance driver and the ambulance are part of the same reference system, the frequency emitted by the ambulance and the frequency heard by the ambulance driver are the same.
The sound source can approach or move away from the observer. The observer can also approach or move away from the sound source. Under these conditions, the following formula is used to determine the frequency of the sound heard by the observer.
|f'=\left(\dfrac{v+v_o}{v-v_s}\right)f|
where
|f’| represents the frequency heard by the observer |(\text{Hz})|
|f| represents the frequency of the wave emitted by the source |(\text{Hz})|
|v| represents the speed of propagation of sound, or |343\ \text{m/s}| in the air
|v_o| represents the speed of the observer |(\text{m/s})|
|v_s| represents the speed of the sound source |(\text{m/s})|
To use this formula, it is assumed that the motions occur in a straight line.
-
If the observer and/or the sound source are at rest, their speed is considered to be |0\ \text{m/s}.|
-
If the observer moves away from the source or the source moves away from the observer, the speed is considered to be less than |0\ \text{m/s}.| It is therefore negative.
-
If the observer moves toward the source or the source moves toward the observer, the speed is considered to be greater than |0\ \text{m/s}.| It is, therefore, positive.
A police car is travelling at a speed of |70{.}2\ \text{km/h}| by emitting a sound with a frequency of |1\ 200\ \text{Hz}.| The police vehicle approaches a stopped car with a motorist inside. What is the frenquency of the sound heard by the motorist?
First, identify the given values and convert the units.
The source of the sound is the police car. The observer is, therefore, the motorist.
|\begin{align}
f&=1\ 200\ \text{Hz}\\
v&=343\ \text{m/s}\\
v_o&=0\ \text{m/s}\ \quad \text{as the motorist is not moving.}\\
v_s&=\dfrac{70{.}2\ \cancel{\text{km}}}{1\ \cancel{\text{h}}} \times \dfrac{1\ 000\ \text{m}}{1\ \cancel{\text{km}}} \times \dfrac{1\ \cancel{\text{h}}}{3\ 600\ \text{s}}\approx 19{.}5\ \text{m/s}\\
f'&= ?\end{align}|
Then, identify the formula to use and replace the given values.
|\begin{align}
f'&=\left(\dfrac{v+v_o}{v-v_s}\right)f\\
f'&=\left(\dfrac{343\ \cancel{\text{m/s}}+0\ \cancel{\text{m/s}}}{343\ \cancel{\text{m/s}}-19{.}5\ \cancel{\text{m/s}}}\right)\times 1\ 200\ \text{Hz}\\
f'&\approx 1\ 272\ \text{Hz}\approx 1{.}27\times10^3\ \text{Hz ou } 1{.}27\ \text{kHz}
\end{align}|
The answer follows the rules of significant digits.
The frequency of the sound heard by the motorist is |1{.}27\ \text{kHz}.| This higher frequency is consistent with the police car approaching the motorist.
A train travelling to the right whistles with a frequency of |700\ \text{Hz}| to announce its arrival at a level crossing. A cyclist already at the level crossing, also heading to the right, is travelling at a speed of |15\ \text{m/s}| and hears the sound at a frequency of |800\ \text{Hz}.| At what speed is the train moving?
First, identify the data.
The source of the sound is the train. The observer is therefore the cyclist.
|\begin{align}
&f'=800\ \text{Hz} &&v=343\ \text{m/s}\\
&f=700\ \text{Hz}&&v_o=-15\ \text{m/s}\\
&&&v_s=?\\
\end{align}|
Speed |v_o| is negative, because the cyclist is not heading towards the train.
Then identify the formula to use and isolate the variable |v_s.|
|\begin{align}
f'&=\left(\dfrac{v+v_o}{v-v_s}\right)f\\
f'(v-v_s)&=(v+v_o)f\\
(v-v_s)&=\dfrac{(v+v_o)f}{f'}\\
v_s&=v-\dfrac{(v+v_o)f}{f'}
\end{align}|
Finally, replace the given values in the formula.
| \begin{align}
v_s&=v-\dfrac{(v+v_o)f}{f'}\\
v_s&=343\ \text{m/s}- \dfrac{\big(343\ \text{m/s}+(-15\ \text{m/s})\big)\times 700\ \cancel{\text{Hz}}}{800\ \cancel{\text{Hz}}}\\
v_s&=56\ \text{m/s}
\end{align}|
The speed of the sound source, the train, is |56\ \text{m/s}.| This positive speed is consistent with the train approaching the cyclist.