L’effet Doppler correspond au phénomène physique selon lequel la fréquence d’une onde est modifiée lorsque la source émettrice de l’onde et/ou l’observateur de l’onde sont en mouvement.
L’effet Doppler affecte les ondes mécaniques, comme le son, et les ondes électromagnétiques, comme la lumière visible.
Lorsqu’une ambulance s’approche d’un piéton, celui-ci entend une sirène plus aigüe que lorsque l’ambulance est immobile. Lorsque l’ambulance s’éloigne du passant, il entend une sirène plus grave.
Dans ces cas, la tonalité du son entendu par le passant est différente de la tonalité du son émis par l’ambulance.

BlurAZ, Shutterstock.com

Sripfoto, Shutterstock.com
Dans le cas des ondes sonores, l’effet Doppler est quantifié différemment en fonction du mouvement de l’observateur et du mouvement de la source sonore. Si l’observateur est au repos, voici comment il entend les sons.
Lorsque l’ambulance (source du son) et l’observateur sont immobiles, l’onde sonore émise par l’ambulance n’est pas affectée. La longueur d’onde |(\lambda)| perçue est alors la même que la longueur d’onde émise par l’ambulance.
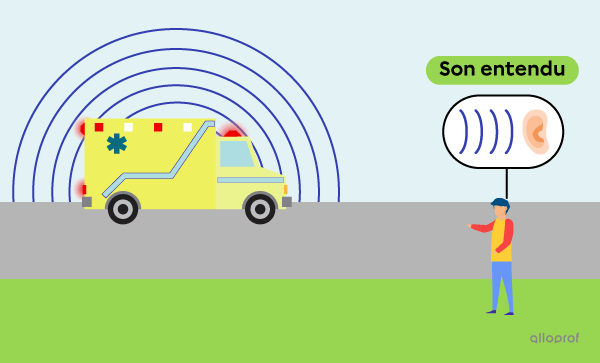
Du point de vue de l’observateur immobile, lorsque l’ambulance se dirige vers lui, les ondes émises se contractent. Cela signifie que pour l’observateur, la longueur d’onde est plus courte et la fréquence, plus grande. Le son est alors plus aigu.
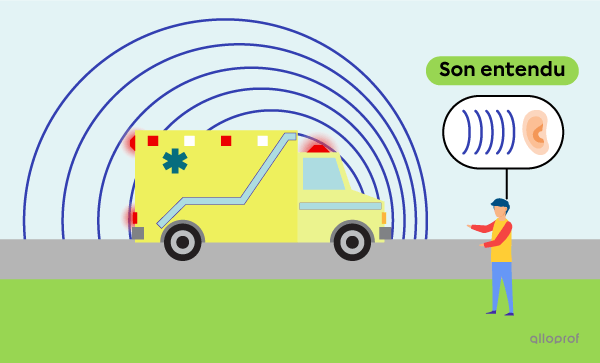
Du point de vue de l’observateur immobile, lorsque l’ambulance s’éloigne de lui, les ondes émises s’allongent. Cela signifie que pour l’observateur, la longueur d’onde est plus grande et la fréquence, plus petite. Le son est alors plus grave.
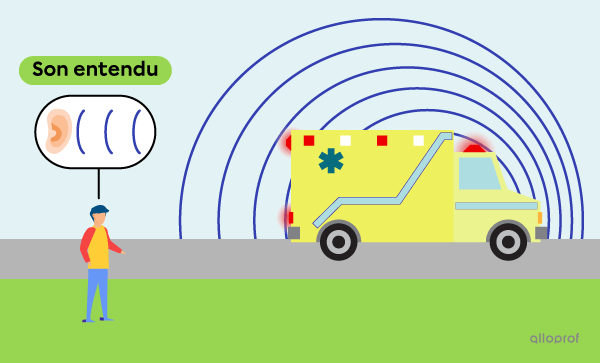
L’effet Doppler est une question de référentiel. Du point de vue de l’ambulancier qui se trouve dans le véhicule, le son entendu est le même que le son émis puisqu’il se déplace à la même vitesse que la source d’émission, soit le véhicule. Autrement dit, puisque l’ambulancier et l’ambulance font partie du même référentiel, la fréquence émise par l’ambulance et la fréquence perçue par l’ambulancier sont les mêmes.
La source sonore peut s’approcher ou s’éloigner de l’observateur. L’inverse est aussi possible, c’est-à-dire que l’observateur peut lui aussi s’approcher ou s’éloigner de la source sonore. Dans ces conditions, on utilise la formule suivante afin de déterminer la fréquence entendue par l’observateur.
|f'=\left(\dfrac{v+v_o}{v-v_s}\right)f|
où
|f’| représente la fréquence entendue par l’observateur |(\text{Hz})|
|f| représente la fréquence de l’onde émise par la source |(\text{Hz})|
|v| représente la vitesse de propagation du son, soit |343\ \text{m/s}| dans l’air
|v_o| représente la vitesse de l’observateur |(\text{m/s})|
|v_s| représente la vitesse de la source du son |(\text{m/s})|
Pour utiliser cette formule, on considère que les déplacements sont effectués en ligne droite.
-
Si l’observateur et/ou la source du son sont immobiles, on considère que leur vitesse est de |0\ \text{m/s}.|
-
Si l’observateur s’éloigne de la source ou que la source s’éloigne de l’observateur, on considère que la vitesse est inférieure à |0\ \text{m/s}.| Elle est donc négative.
-
Si l’observateur s’approche de la source ou que la source s’approche de l’observateur, on considère que la vitesse est supérieure à |0\ \text{m/s}.| Elle est donc positive.
Une voiture de police circule à une vitesse de |70{,}2\ \text{km/h}| en émettant un son dont la fréquence est de |1\ 200\ \text{Hz}.| Ce véhicule policier s’approche de la voiture d’un automobiliste à l’arrêt. Quelle est la fréquence du son entendu par l’automobiliste?
D’abord, on identifie les données et on convertit les unités.
La source du son est la voiture de police. L’observateur est donc l’automobiliste.
|\begin{align}
f&=1\ 200\ \text{Hz}\\
v&=343\ \text{m/s}\\
v_o&=0\ \text{m/s}\ \quad \text{car l'automobiliste est immobile.}\\
v_s&=\dfrac{70{,}2\ \cancel{\text{km}}}{1\ \cancel{\text{h}}} \times \dfrac{1\ 000\ \text{m}}{1\ \cancel{\text{km}}} \times \dfrac{1\ \cancel{\text{h}}}{3\ 600\ \text{s}}\approx 19{,}5\ \text{m/s}\\
f'&= ?\end{align}|
On identifie ensuite la formule à utiliser et on remplace les données.
|\begin{align}
f'&=\left(\dfrac{v+v_o}{v-v_s}\right)f\\
f'&=\left(\dfrac{343\ \cancel{\text{m/s}}+0\ \cancel{\text{m/s}}}{343\ \cancel{\text{m/s}}-19{,}5\ \cancel{\text{m/s}}}\right)\times 1\ 200\ \text{Hz}\\
f'&\approx 1\ 272\ \text{Hz}\approx 1{,}27\times10^3\ \text{Hz ou } 1{,}27\ \text{kHz}
\end{align}|
La réponse respecte les règles des chiffres significatifs.
La fréquence du son entendu par l’automobiliste est de |1{,}27\ \text{kHz}.| Cette fréquence plus élevée est cohérente avec le fait que la voiture de police s’approche de l’automobiliste.
Un train circulant vers la droite siffle avec une fréquence de |700\ \text{Hz}| pour annoncer son arrivée à un passage à niveau. Un cycliste déjà au passage à niveau, allant lui aussi vers la droite, circule à une vitesse de |15\ \text{m/s}| et entend le son à une fréquence de |800\ \text{Hz}.| Quelle est la vitesse du train?
D’abord, on identifie les données.
La source du son est le train. L’observateur est donc le cycliste.
|\begin{align}
&f'=800\ \text{Hz} &&v=343\ \text{m/s}\\
&f=700\ \text{Hz}&&v_o=-15\ \text{m/s}\\
&&&v_s=?\\
\end{align}|
La vitesse |v_o| est négative, car le cycliste ne se dirige pas vers le train.
On identifie ensuite la formule à utiliser et on isole la variable |v_s.|
|\begin{align}
f'&=\left(\dfrac{v+v_o}{v-v_s}\right)f\\
f'(v-v_s)&=(v+v_o)f\\
(v-v_s)&=\dfrac{(v+v_o)f}{f'}\\
v_s&=v-\dfrac{(v+v_o)f}{f'}
\end{align}|
On remplace finalement les données dans la formule.
| \begin{align}
v_s&=v-\dfrac{(v+v_o)f}{f'}\\
v_s&=343\ \text{m/s}- \dfrac{\big(343\ \text{m/s}+(-15\ \text{m/s})\big)\times 700\ \cancel{\text{Hz}}}{800\ \cancel{\text{Hz}}}\\
v_s&=56\ \text{m/s}
\end{align}|
La vitesse de la source sonore, soit le train, est de |56\ \text{m/s}.| Cette vitesse positive est cohérente avec le fait que le train s’approche du cycliste.