This concept sheet explains the procedure to follow to determine the measurement of the density of a substance.
Density is used to determine the ratio between the mass and the volume of a substance. Since this property is characteristic (each substance has its own density), determining this value for an unknown substance will eventually lead to its identification.
The procedure to be followed to identify the density depends on the state of the substance.
-
140 mL syringe
-
Stopper
-
Nail
-
Beam balance
-
Unknown gas
-
Lab coat
-
Safety glasses

-
Evacuate the syringe by pushing the plunger.
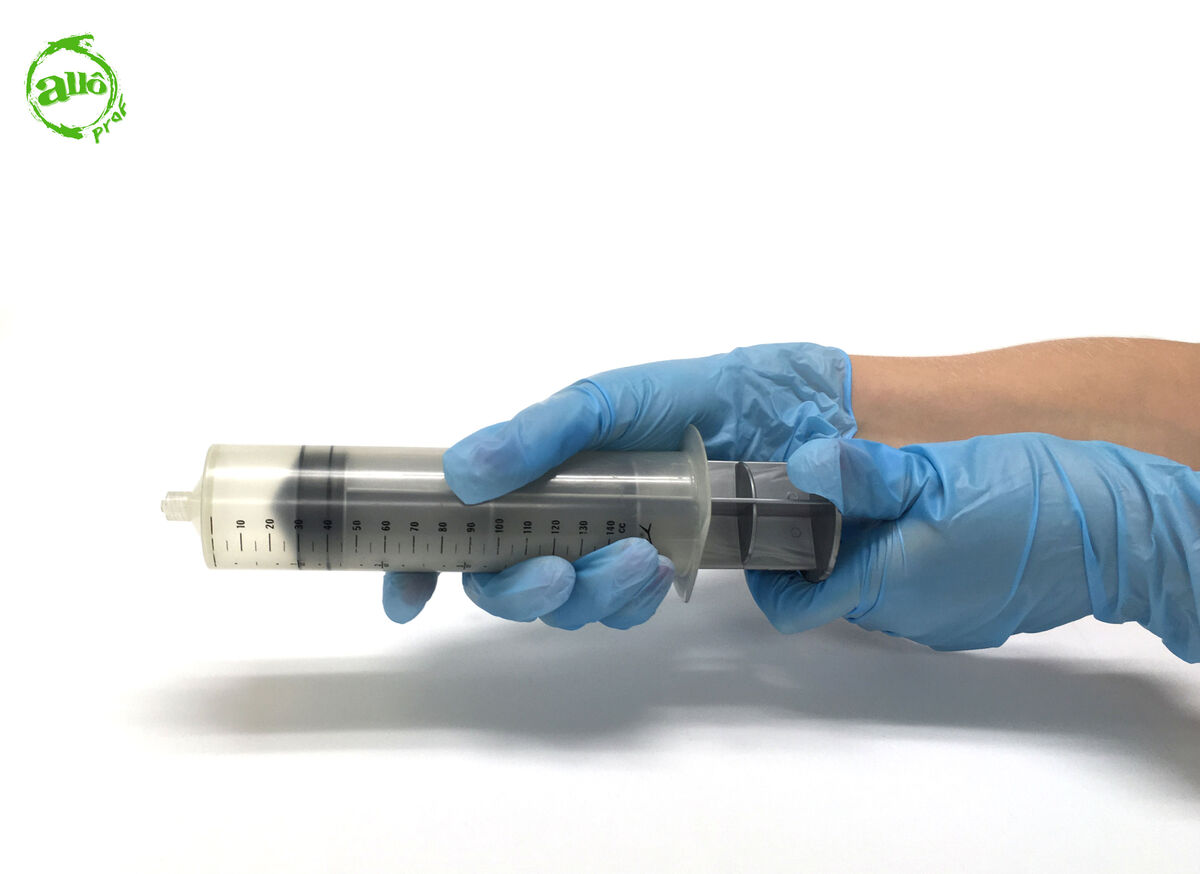
-
Put the stopper on the tip of the syringe.
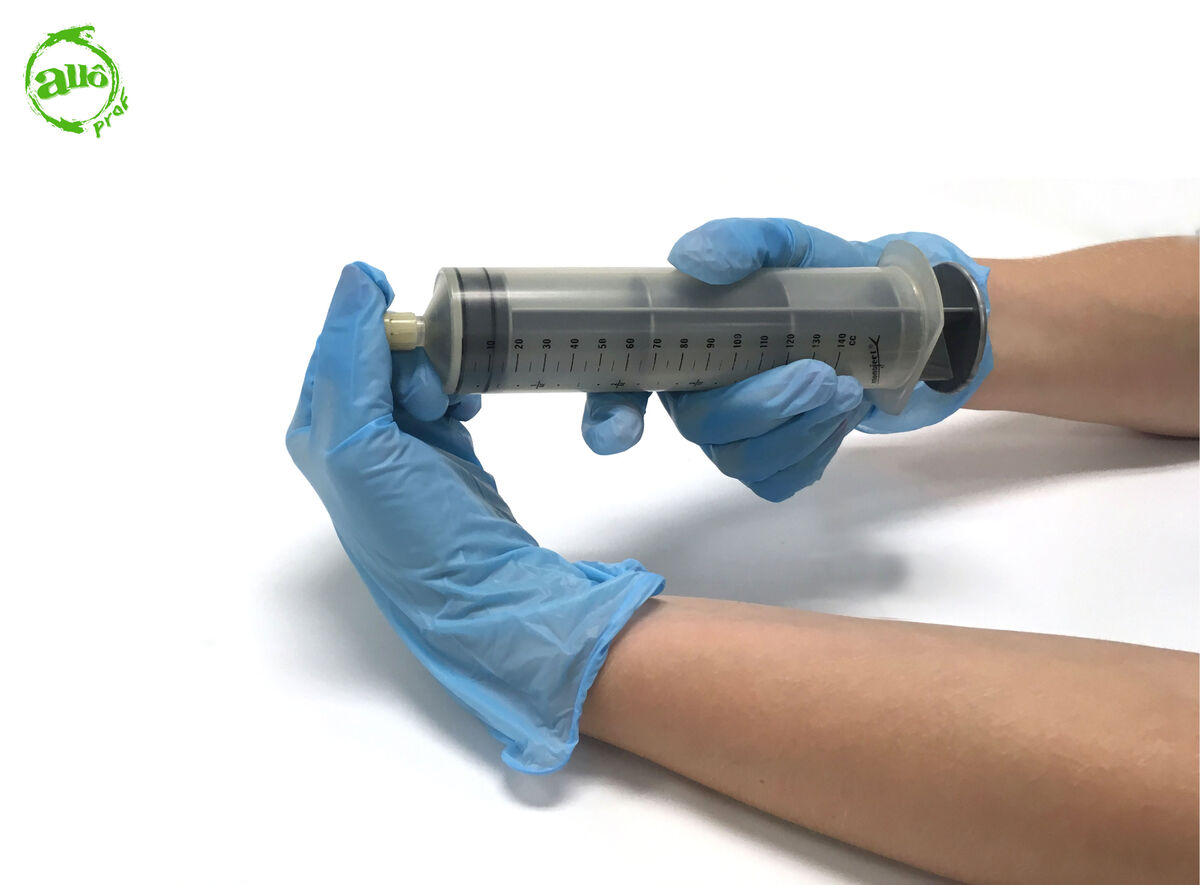
-
Pull back on the plunger until the maximum volume of the syringe is reached.

-
Insert the nail into the hole located on the plunger.
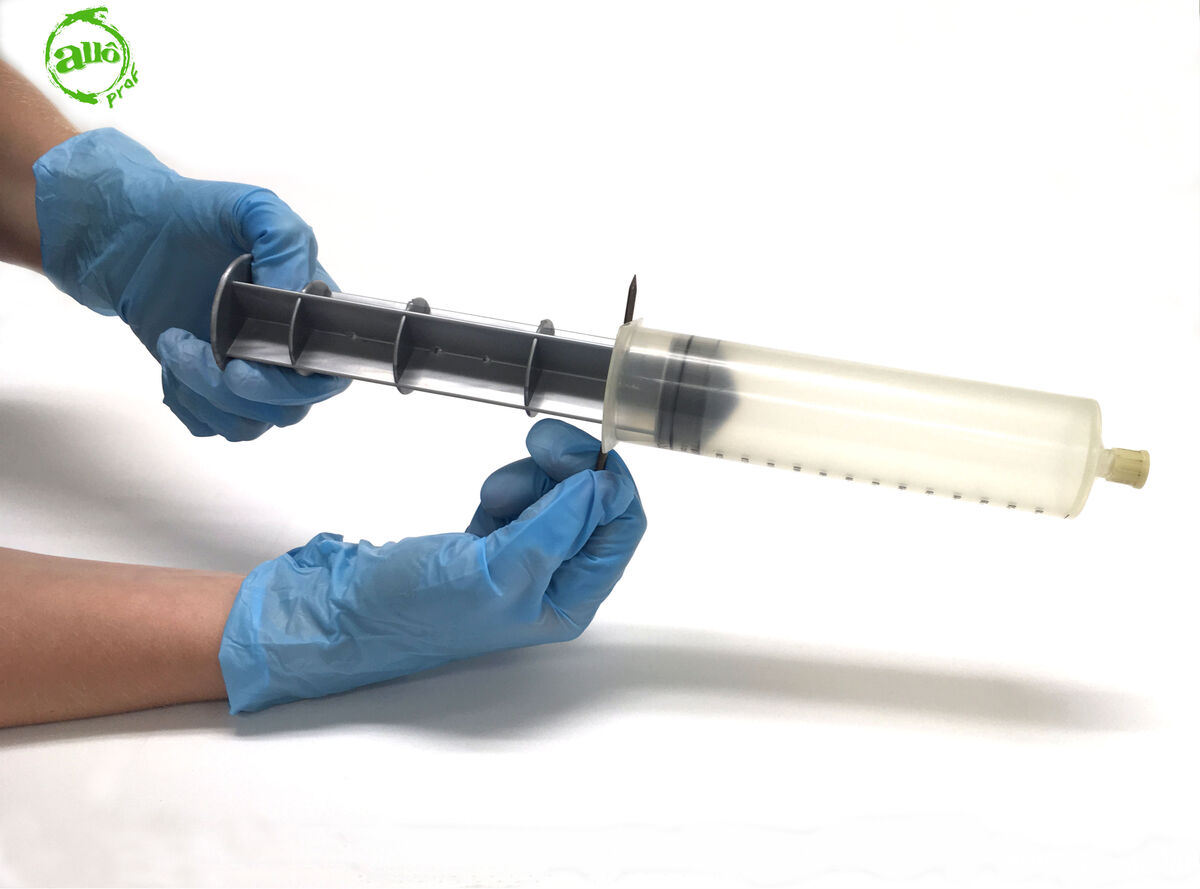
It is best to perform this step with a teammate to avoid accidents.
-
Weigh the empty syringe with the beam balance and record its mass.

-
Fill the syringe with the unknown gas until the maximum gas volume is reached.
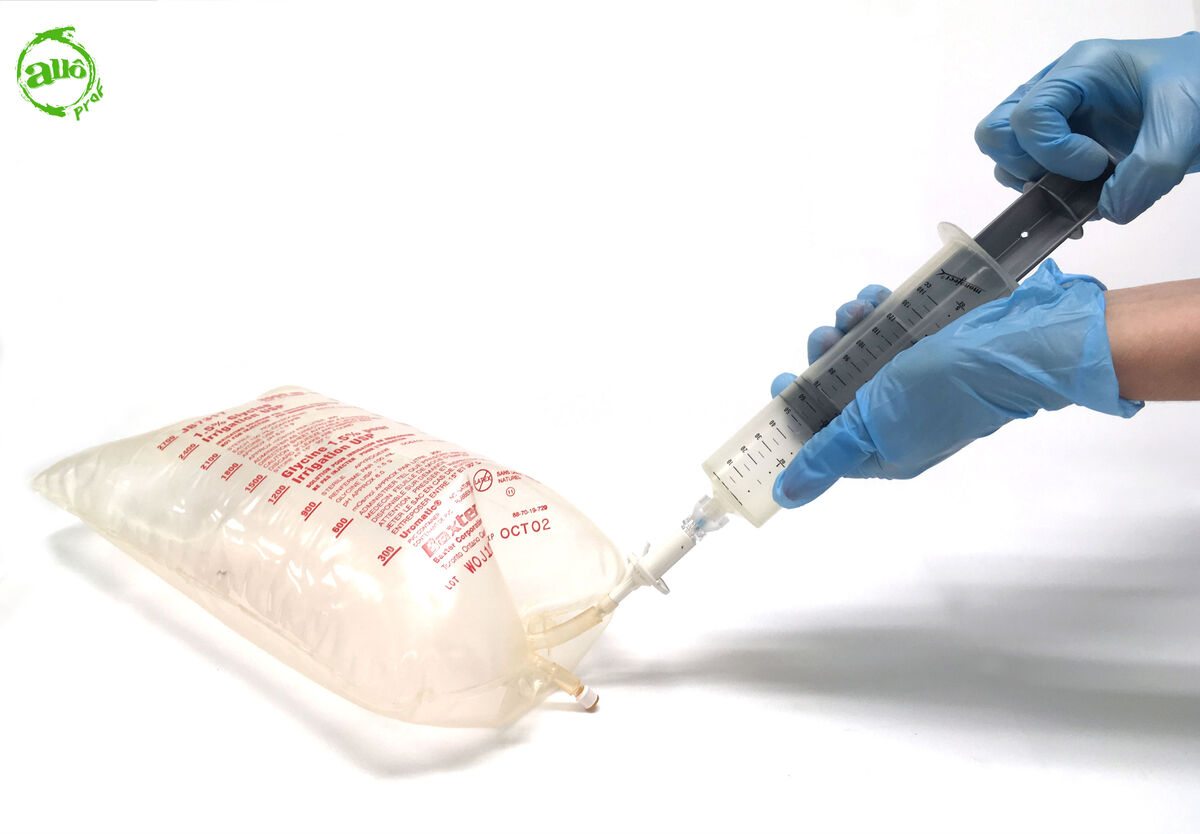
-
Put the stopper and nail back in place.
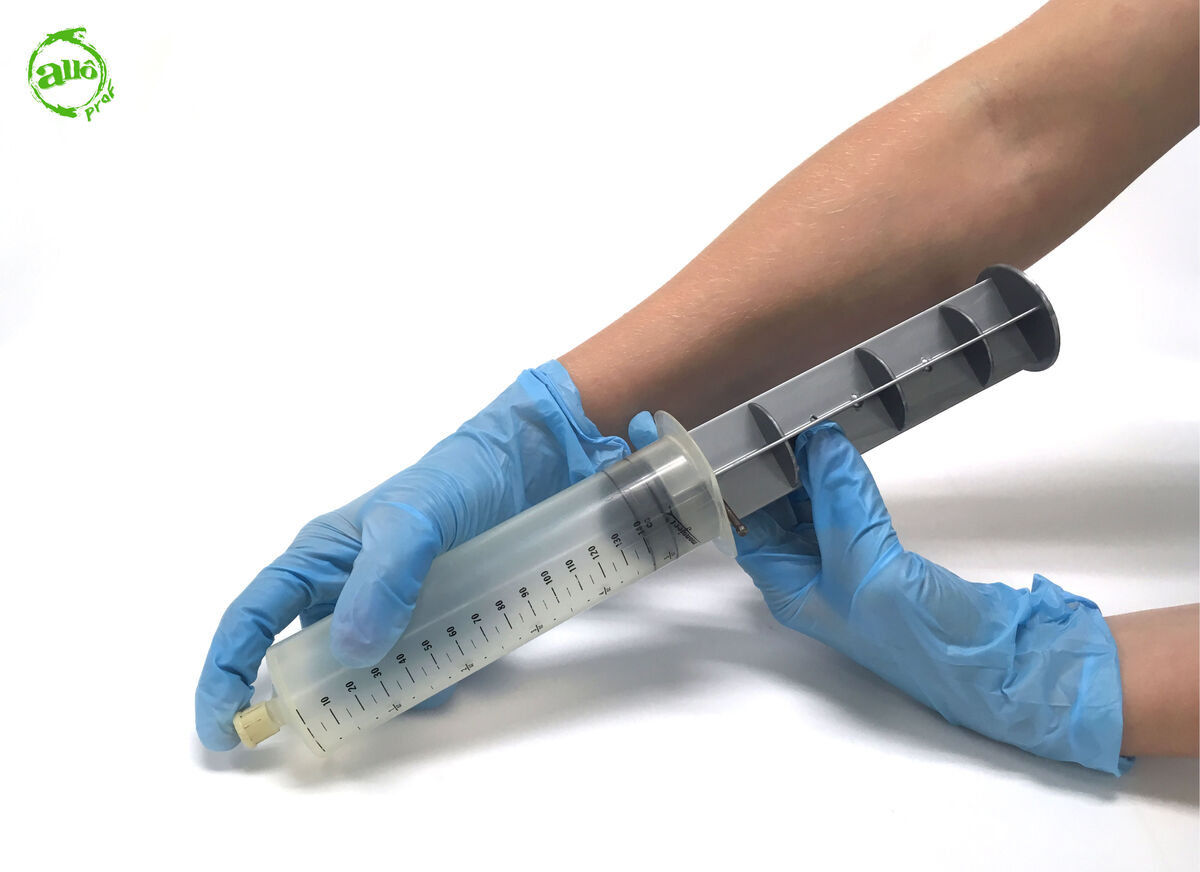
-
Weigh the syringe using the beam balance and record its mass.

-
Calculate the mass of the unknown gas.
-
Calculate the density of the unknown gas.
-
Put away the equipment.
Given the hazards associated with some gases, always make sure that the gas can be released into the classroom.
To determine the density of a gaseous substance, it is necessary to calculate the ratio between the mass and the volume of the gas. The volume is easily determined by the amount of gas placed inside the syringe (in the above experiment, this volume was 140 mL).
To find out the mass of the gas, subtract the mass of the syringe (step 4) from the mass of the syringe with the unknown gas (step 7).
|{m}_ {{gas}}={m}_ {{syringe + gas}}-{m}_ {{syringe}}|
|{m}_ {{gas}}| represents the mass of the gas |(\text {g})|
|{m}_ {{syringe + gas}}| represents the mass of the gas and the syringe |(\text {g})|
|{m}_ {{syringe}}| represents the mass of the empty syringe |(\text {g})|
When the mass has been determined, the last step is to calculate the density.
|\rho =\displaystyle \frac {{m}_ {\text{gas}}}{{V}_ {{gas}}}|
|\rho| represents the density of the gas |(\text {g/mL})|
|{m}_ {{gas}}| represents the mass of the gas |(\text {g})|
|{{V}_ {{gas}}}| represents the volume of gas |(\text {mL})|
It is important to record all experimental results in a results table. Here is an example of a table template that can be presented.
Density of an Unknown Gas
| | Unknown gas |
| |{m}_ {{syringe}}| | |\text {g}| |
| |{m}_ {{syringe + gas}}| | |\text {g}| |
| |{{V}_ {{gas}}}| | |\text {mL}| |
| |{m}_ {{gas}}| | |\text {g}| |
| |\rho| | |\text {g/mL}| |
Since density is a characteristic property, it is possible to compare the density value obtained in the experiment with theoretical values.
The following concept sheet presents the density of certain gases.
Density of Gases
The following concept sheet explains what density is.
Density
-
10 mL graduated cylinder
-
Beam balance
-
Unknown liquid
-
Lab coat
-
Safety glasses

-
Weigh the empty graduated cylinder using the beam balance and record its mass.

-
Pour 10 mL of the unknown liquid into the graduated cylinder.

In order to obtain maximum precision, the use of a dropper is recommended.
-
Weigh the graduated cylinder with the liquid using the beam balance. Record the mass.

-
Calculate the mass of the liquid.
-
Calculate the density of the liquid.
-
Clean and store the equipment.
Given the dangers caused by some liquids, it is best to check where the liquid is to be disposed of in order to ensure proper handling.
To determine the density of a liquid substance, calculate the ratio between the mass and the volume of the liquid. The volume used is known, as it represents the quantity of liquid placed in the graduated cylinder (in the experiment shown above, this volume was 10 mL).
To find out the mass of the liquid, subtract the mass of the empty graduated cylinder (step 1) from the mass of the graduated cylinder containing the unknown liquid (step 3).
|{m}_ {{liquid}}={m}_ {{graduated \: cylinder + liquid}}-{m}_ {{graduated \: cylinder}}|
|{m}_ {{liquid}}| represents the mass of the liquid |(\text {g})|
|{m}_ {{graduated \: cylinder + liquid }}| represents the mass of the liquid and the graduated cylinder |(\text {g})|
|{m}_ {{graduated \: cylinder}}| represents the mass of the empty graduated cylinder |(\text {g})|
Once the mass of the liquid has been calculated, all that is left is to calculate its density.
|\rho=\displaystyle \frac {{m}_ {{liquid}}}{{V}_ {{liquid}}}|
|\rho| represents the density of the liquid |(\text {g/mL})|
|{m}_ {{liquid}}| represents the mass of the liquid |(\text {g})|
|{{V}_ {{liquid}}}| represents the volume of the liquid |(\text {mL})|
A results table is essential to present the results obtained in the experiment. Here is an example of a table template that can be presented.
Density of an Unknown Liquid
| | Unknown liquid |
| |{m}_ {{graduated cylinder}}| | |\text {g}| |
| |{m}_ {{graduated cylinder + liquid}}| | |\text {g}| |
| |{{V}_ {{liquid}}}| | |\text {mL}| |
| |{m}_ {{liquid}}| | |\text {g}| |
| |\rho| | |\text {g/mL}| |
The unknown liquid can be identified by density, as this is a characteristic property. If the substance is known, it is possible to assess the quality of the procedure by comparing the experimental value with the by comparing the experimental value with the value found in tables.
The following concept sheet gives information on the density of certain liquids.
Density of Liquids
The following concept sheet explains what density is.
Density
-
100 mL graduated cylinder
-
Water
-
Beam balance
-
Unknown solid
-
Lab coat
-
Safety glasses

-
Weigh the unknown solid using the beam balance.

-
Add 50 mL of water into the graduated cylinder.


To obtain maximum precision, the use of a dropper is recommended.
-
Gently slide the solid object into the graduated cylinder.
It is important to take your time to do this step. If the object is inserted into the water too quickly, the water could splash out of the graduated cylinder, which could affect the results.
-
Record the total water volume.

-
Calculate the volume of the unknown solid.
-
Calculate the density of the unknown solid.
-
Put away the equipment.
The density of a solid substance can be determined by calculating the ratio between the mass of the solid and its volume. The mass was determined in the first step using the balance. To find the volume, determine the water displacement, which is the difference between the volume of water with the unknown solid (step 4) and the volume of water initially present in the graduated cylinder (in the above experiment, this volume was 50 mL).
|{V}_ {{solid}}={V}_ {{water + solid}}-{V}_ {{water}}|
|{V}_ {{solid}}| represents the volume of the solid |(\text {mL})|
|{V}_ {{water + solid}}| represents the volume of water and solid |(\text {mL})|
|{V}_ {{water}}| represents the volume of water poured into the graduated cylinder initially |(\text {mL})|
Once the volume has been calculated, the ratio between the mass and the volume provides the most important data, namely the density of the solid.
|\rho =\displaystyle \frac {{m}_ {{solid}}}{{V}_ {{solid}}}|
|\rho| represents the density of the solid |(\text {g/mL})|
|{m}_ {{solid}}| represents the mass of the solid |(\text {g})|
|{{V}_ {{solid}}}| represents the volume of the solid |(\text {mL})|
In order to present clear experimental results, it is important to create a table of the results.
Density of an Unknown Solid
| | Unknown solid |
| |{m}_ {{solid}}| | |\text {g}| |
| |{V}_ {{water}}| | |\text {mL}|l |
| |{{V}_ {{water + solid}}}| | |\text {mL}| |
| |{V}_ {{solid}}| | |\text {mL}| |
| |\rho| | |\text {g/mL}| |
Finally, the density value can be used either to identify an unknown substance or, if the substance is known, to assess the quality of the procedure.
The following concept sheet provides information on the density of certain solids.
Density of Solids
The following concept sheet explains what density is.
Density