The law of conservation of energy states that energy cannot be created nor destroyed. It can only be transformed from one form to another or transferred from one place to another.
Just as matter is conserved during a chemical reaction and complies with the law of conservation of matter, energy also complies with Lavoisier's famous phrase:
"Nothing is lost, nothing is created, everything is transformed!"
Thus, according to this law, the transfers and transformations of energy take place without loss of energy.
However, it is important to note that this law can be observed only if it takes place in an isolated system.
An isolated system is a system that does not carry out any exchange of matter or energy with its environment.
A thermos is an isolated system because it stores its contents (like hot chocolate) and its energy (the heat of the hot chocolate) without any exchange with the outside.

Such a system ensures that all of the initial energies are equal to all of the final energies.
On the other hand, an open system allows for exchanges of matter and energy with the environment. A closed system conserves all the matter involved without conserving the energy involved. These two types of systems do not respect the law of conservation of energy.
A bowl of soup is an open system since it allows exchanges of matter and energy with its environment.

A freezer is a closed system because even though it releases energy in the form of heat, it keeps all food cool.
The law of conservation of energy makes it possible to study energy transfers and transformations.
When we hold a mug of hot chocolate, the thermal energy of the hot chocolate is transferred from the mug to our hand.

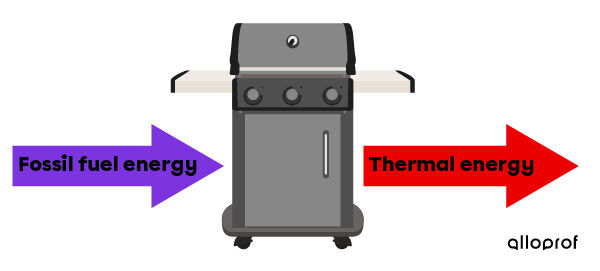
A barbecue transforms the fossil fuel energy that comes from propane or charcoal into thermal energy for cooking food.
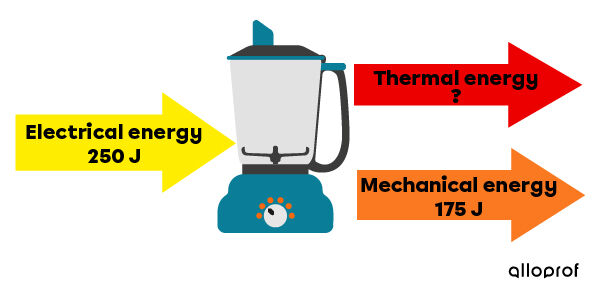
A mixer consumes |250\ \text{J}| of electrical energy. If the device uses |175\ \text{J}| of this energy as mechanical energy and the rest of the energy is dispersed into the environment in the form of thermal energy, what quantity of thermal energy is released by the mixer?
|\begin{align}\text{E}_{\text{electrical}}&=\text{E}_{\text{thermal}}+\text{E}_{\text{mechanical}}\\\text{E}_{\text{thermal}}&=\text{E}_{\text{electrical}}-\text{E}_{\text{mechanical}}\\\text{E}_{\text{thermal}}&=250\ \text{J}-175\ \text{J}\\\text{E}_{\text{thermal}}&=75\ \text{J}\end{align}|
The mixer releases |75\ \text{J}| of thermal energy.
A cart moves on the rail of a roller coaster. Assuming that there is no friction, it is possible to determine the different forms of energy present in different places.
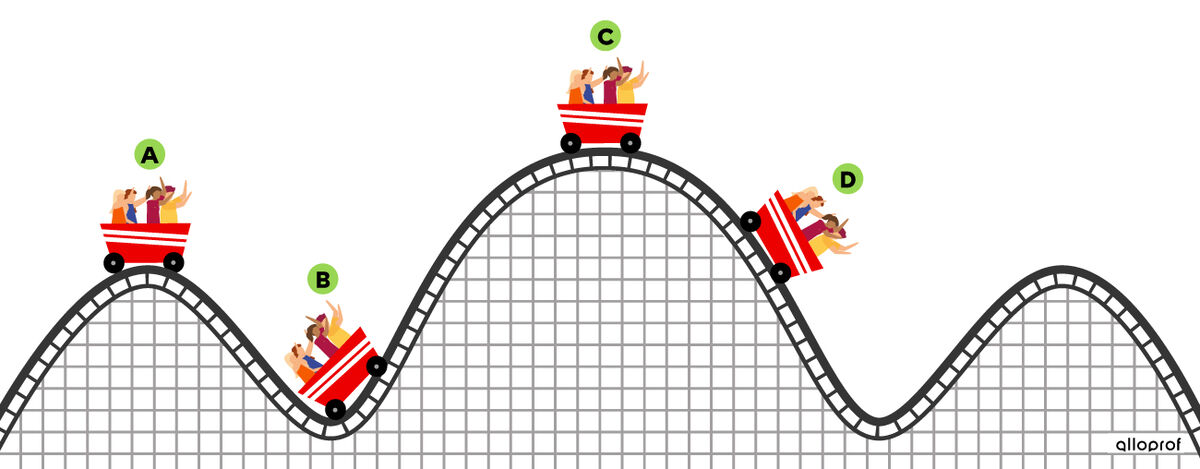
The motion of the cart at point A gives an amount of kinetic energy equal to |100\ \text{J}|. Furthermore, its height gives it an amount of potential energy equal to |100\ \text{J}|. The mechanical energy of this cart corresponds to the sum of the quantities of kinetic and potential energy, namely:
|E_{k} = 100\ \text{J}| , |E_{p} = 100\ \text{J}| , |E_{m} = 100\ \text{J} + 100\ \text{J} = 200\ \text{J}|
At point B, the height of the cart from the ground decreased, which means that the potential energy of the cart also decreased. Since there can be no loss of energy, this potential energy was transformed into kinetic energy. The kinetic energy has, therefore, increased.
|E_{k} = 200\ \text{J}| , |E_{p} = 0\ \text{J}| , |E_{m} = 200\ \text{J} + 0\ \text{J} = 200\ \text{J}|
At point C, the height of the cart above the ground increased, while its speed decreased. Since there can be no loss of energy, it means that the kinetic energy of the cart was transformed into potential energy.
|E_{k} = 10\ \text{J}| , |E_{p} = 190\ \text{J}| , |E_{m} = 10\ \text{J} + 190\ \text{J} = 200\ \text{J}|
At point D, the cart returns to the same height as its starting point. It, therefore, has the same amount of energy that it had at point A.
|E_{k} = 100\ \text{J}| , |E_{p} = 100\ \text{J}| , |E_{m} = 100\ \text{J} + 100\ \text{J} = 200\ \text{J}|
The amount of mechanical energy is conserved because the amount of energy at the start is the same throughout the motion of the cart. Indeed, "nothing is lost, nothing is created, everything is transformed."