La loi de la conservation de l'énergie stipule que l'énergie ne peut être ni créée ni détruite. Elle ne peut être que transformée d'une forme à une autre ou transférée d'un endroit à un autre.
Un peu comme la matière se conserve au cours d'une réaction chimique et respecte la loi de la conservation de la matière, l'énergie respecte aussi la célèbre phrase de Lavoisier :
« Rien ne se perd, rien ne se crée, tout se transforme! »
Ainsi, selon cette loi, les transferts et les transformations d'énergie se déroulent sans perte d'énergie.
Pour que cette loi soit respectée, il est toutefois important d'être en présence d'un système isolé.
Un système isolé est un système qui n'effectue aucun échange de matière ni d'énergie avec son environnement.
Un thermos est un système isolé, car ce contenant permet de conserver le contenu (comme un chocolat chaud) et l'énergie (la chaleur du chocolat chaud) sans que des échanges ne se produisent avec l'extérieur.

Un tel système assure que la totalité des énergies initiales est égale à la totalité des énergies finales obtenues.
À l’inverse, un système ouvert permet des échanges de matière et d’énergie avec l’environnement. Un système fermé, quant à lui, conserve toute la matière impliquée sans toutefois conserver l’énergie en jeu. Ces deux types de systèmes ne permettent pas de respecter la loi de la conservation de l’énergie.
Un bol de soupe est un système ouvert puisqu’il permet des échanges de matière et d’énergie avec son environnement.

Un congélateur est un système fermé, car même s’il diffuse de l’énergie sous forme de chaleur, il conserve toute la nourriture au frais.
La loi de la conservation de l'énergie permet d'étudier les transferts et les transformations d'énergie.
Lorsqu’on tient une tasse de chocolat chaud, l’énergie thermique du chocolat chaud est transférée de la tasse à notre main.

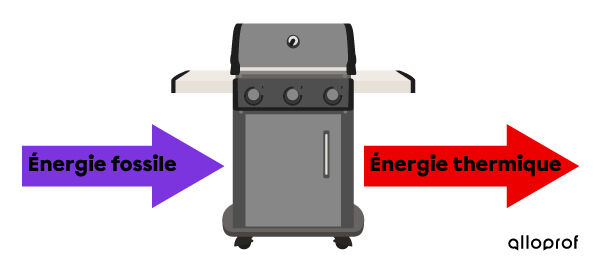
Un barbecue transforme l’énergie fossile qui provient du propane ou du charbon en énergie thermique pour cuire les aliments.
Un mélangeur consomme |250\ \text{J}| d’énergie électrique. S’il utilise |175\ \text{J}| de cette énergie en énergie mécanique et que le reste de l’énergie est dissipé dans l’environnement sous forme d’énergie thermique, quelle est la quantité d’énergie thermique dégagée par le mélangeur?
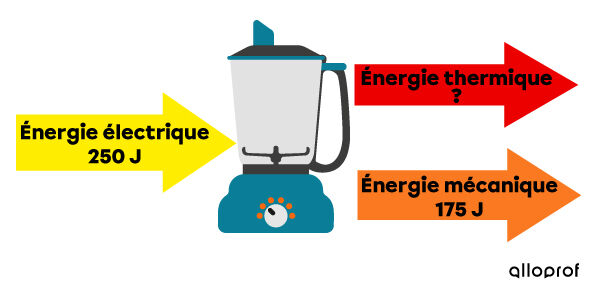
|\begin{align}\text{E}_{\text{électrique}}&=\text{E}_{\text{thermique}}+\text{E}_{\text{mécanique}}\\\text{E}_{\text{thermique}}&=\text{E}_{\text{électrique}}-\text{E}_{\text{mécanique}}\\\text{E}_{\text{thermique}}&=250\ \text{J}-175\ \text{J}\\\text{E}_{\text{thermique}}&=75\ \text{J}\end{align}|
Le mélangeur dégage |75\ \text{J}| d’énergie thermique.
Un charriot se déplace sur le rail d'une montagne russe. En supposant qu'il n'y ait aucun frottement, il est possible de déterminer les différentes formes d'énergie présentes aux différents endroits.
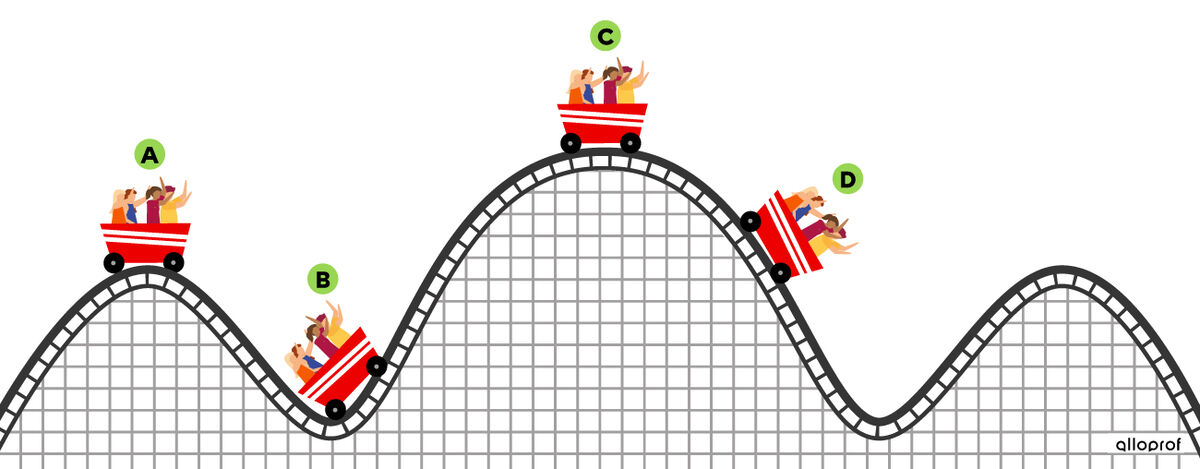
Le mouvement du charriot au point A lui donne une quantité d'énergie cinétique égale à |100\ \text{J}|. De plus, sa hauteur lui donne une quantité d'énergie potentielle égale à |100\ \text{J}|. L’énergie mécanique de ce charriot correspond à la somme des quantités d’énergie cinétique et potentielle, soit :
|E_{k} = 100\ \text{J}|, |E_{p} = 100\ \text{J}|, |E_{m} = 100\ \text{J} + 100\ \text{J} = 200\ \text{J}|
Au point B, la hauteur du charriot par rapport au sol a diminué, ce qui signifie que l’énergie potentielle du charriot a diminué. Puisqu’il ne peut pas y avoir de perte d’énergie, cette énergie potentielle a été transformée en énergie cinétique. L'énergie cinétique a donc augmenté.
|E_{k} = 200\ \text{J}|, |E_{p} = 0\ \text{J}|, |E_{m} = 200\ \text{J} + 0\ \text{J} = 200\ \text{J}|
Au point C, la hauteur du charriot par rapport au sol a augmenté, alors que sa vitesse a diminué. Puisqu’il ne peut pas y avoir de perte d’énergie, cela signifie que l’énergie cinétique du charriot a été transformée en énergie potentielle.
|E_{k} = 10\ \text{J}|, |E_{p} = 190\ \text{J}|, |E_{m} = 10\ \text{J} + 190\ \text{J} = 200\ \text{J}|
Au point D, le charriot revient à la même hauteur que son point de départ. Il possède donc les mêmes quantités d'énergie que celles qu'il avait au point A.
|E_{k} = 100\ \text{J}|, |E_{p} = 100\ \text{J}|, |E_{m} = 100\ \text{J} + 100\ \text{J} = 200\ \text{J}|
La quantité d’énergie mécanique est conservée, car la quantité d'énergie au départ est la même tout au long du déplacement du charriot. En effet, « rien ne se perd, rien ne se crée, tout se transforme ».