Dans certaines situations, il sera question de trouver la chaine de poids minimal reliant deux points en particulier dans un graphe valué. Cette chaine de poids minimal porte aussi le nom de chaine optimale.
Étapes pour la recherche de la chaine optimale entre deux sommets dans un graphe valué :
-
Assigner à chaque sommet adjacent à celui de départ une lettre et un nombre représentant respectivement le sommet de provenance et le poids de la plus petite chaine qui les relie.
-
Répéter la première étape jusqu'au sommet d'arrivée.
-
Procéder à rebours pour reconstituer la chaine optimale en partant du dernier sommet jusqu'au sommet de départ.
Le chemin le plus court
Voici le plan d'un quartier regroupant 7 immeubles. Laurie réside dans l'immeuble A et elle veut se rendre chez son amie Jessica, qui habite dans l'immeuble G, en empruntant le chemin le plus court. Par où doit-elle passer et combien de temps est-ce que ça devrait lui prendre si les valeurs indiquées sur le graphe suivant sont les durées de déplacement (en minutes)?
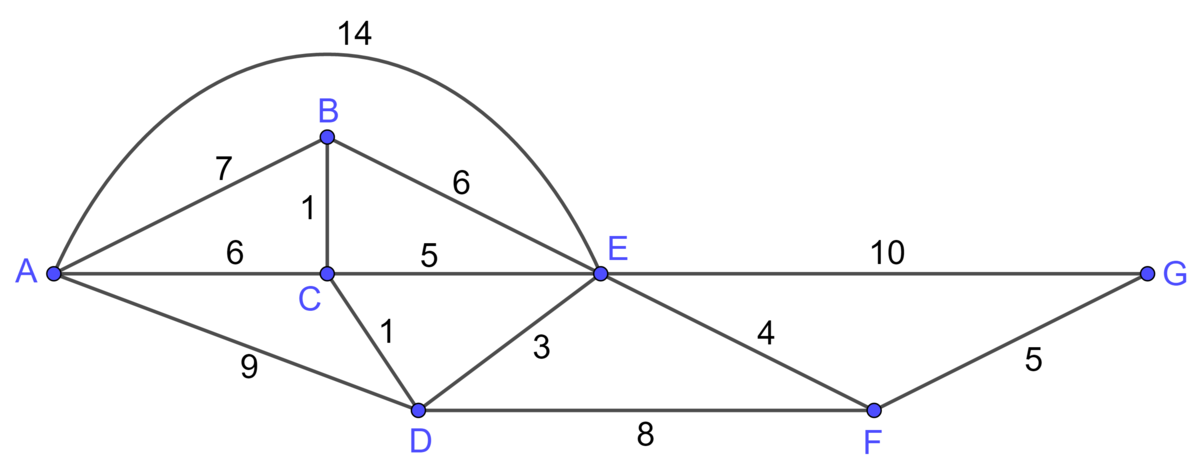
Solution
1. Assigner, à chaque sommet adjacent à celui de départ, une lettre et un nombre représentant respectivement le sommet de provenance et le poids de la plus petite chaine qui les relie.
Le sommet A est le sommet de départ. Les sommets adjacents sont B, C, D et E. On recherche donc la chaine ayant la plus petite valeur reliant chacun de ces sommets au sommet de départ.
Pour le sommet B, la chaine ayant la plus petite valeur, |7|, est celle provenant directement de A. On inscrit donc |\color{red}{7(A)}| juste à côté du sommet B. Pour C, la chaine ayant la plus petite valeur, |6|, provient directement de A. On inscrit donc |\color{red}{6(A)}| juste à côté du sommet C. Pour D, la chaine provenant directement du sommet A a une valeur de |9|, mais celle passant par le sommet C a une valeur plus petite, soit |6+1=7|. On choisit donc cette dernière en inscrivant |\color{red}{7(C)}|. Pour E, la chaine ayant la plus petite valeur est celle passant par C puis par D, avec une valeur de |6+1+3=10|. On y inscrit |\color{red}{10(D)}|.
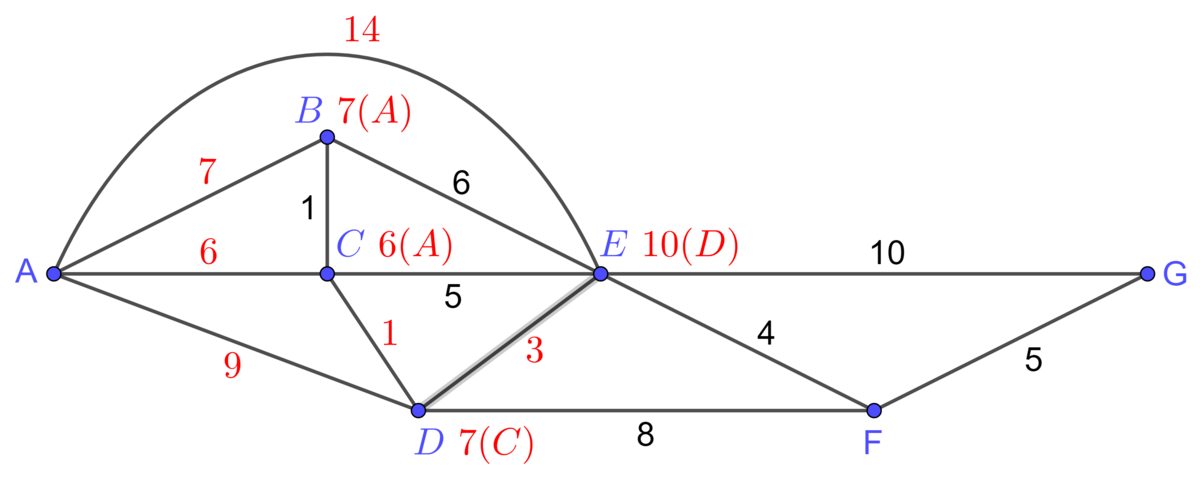
2. Répéter la première étape jusqu'au sommet d'arrivée.
Comme nous avons évalué les sommets B, C, D, E, nous devons maintenant appliquer la même procédure aux sommets adjacents, soit F et G.
Pour F, la chaine provenant de D a une valeur de |7+8=15| et celle provenant de E a une valeur de |10+4=14|.On choisit donc la chaine issue du sommet E en inscrivant |\color{red}{14(E)}| à côté de F. Pour G, en procédant de la même façon, on trouve que la chaine de poids minimal est celle provenant du sommet F, avec une valeur de |14+5=19|. On y inscrit donc |\color{red}{19(F)}|.
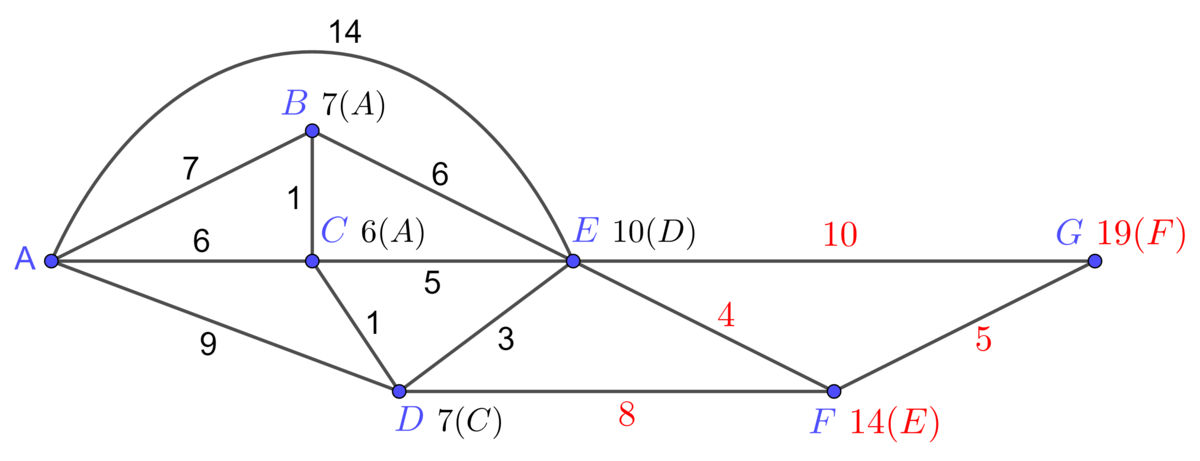
3. Procéder à rebours pour reconstituer la chaine optimal en partant du dernier sommet jusqu'au sommet de départ.
En partant du dernier sommet G, on suit les indications que nous avons inscrit à côté de chaque sommet pour reconstituer la chaine de poids minimal jusqu'au sommet de départ.
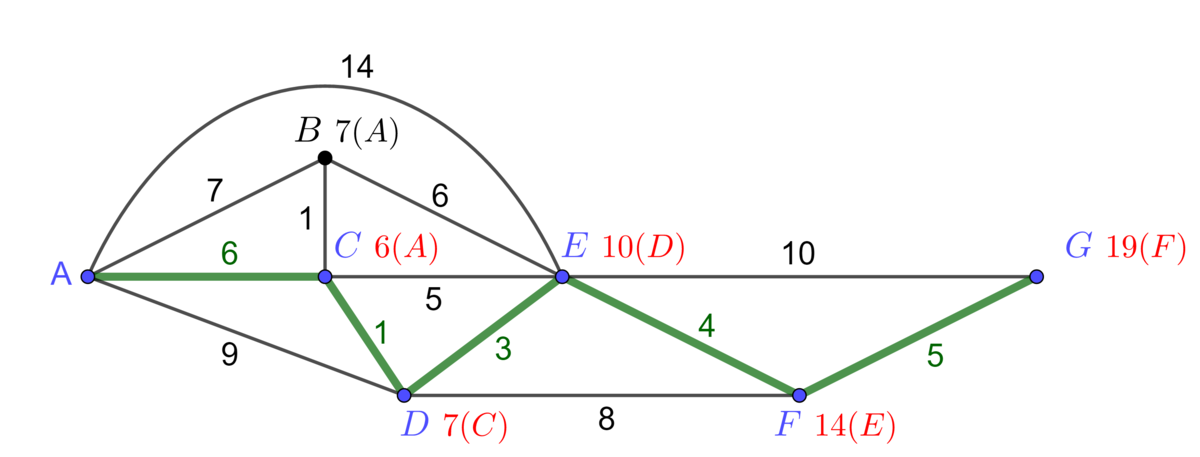
La chaine optimale recherchée est donc la chaine A-C-D-E-F-G. C'est alors le trajet que Laurie devra emprunter pour se rendre le plus rapidement possible chez Jessica. Elle devrait y être en |19| minutes.
En regardant l'exemple précédent, on remarque que ce n'est pas nécessairement la ligne droite qui est la plus courte. En effet, le trajet A-C-E-G a une valeur totale de |20| minutes comparativement au trajet de |19| minutes que nous avions trouvé. Ce n'est pas non plus le trajet qui compte le moins d'étapes qui est le plus court, car A-E-G n'a que 2 étapes et est d'une durée de |24| minutes.
Un algorithme semblable à la démarche employée pour résoudre le problème précédent est programmé dans les applications de GPS de nos téléphones intelligents.