The Path of Minimum Value

Steps for finding the path of minimum value (shortest path) between two vertices in a weighted graph

1. Assign to each vertex that is adjacent to the starting vertex a letter and a number representing the previous vertex and the weight of the smallest path that connects them.

2. Repeat the first step until the final vertex is reached.

3. Work backwards to reconstruct the shortest path, moving from the last vertex to the starting vertex.

The shortest path

Here is the layout of a neighbourhood that includes |7| buildings. Laurie lives in Building |A| and she wants to visit her friend Jessica, who lives in Building |G|, by taking the shortest path. By where should she pass and how long should it take her if the values shown in the following graph represent the travel times (in minutes)?

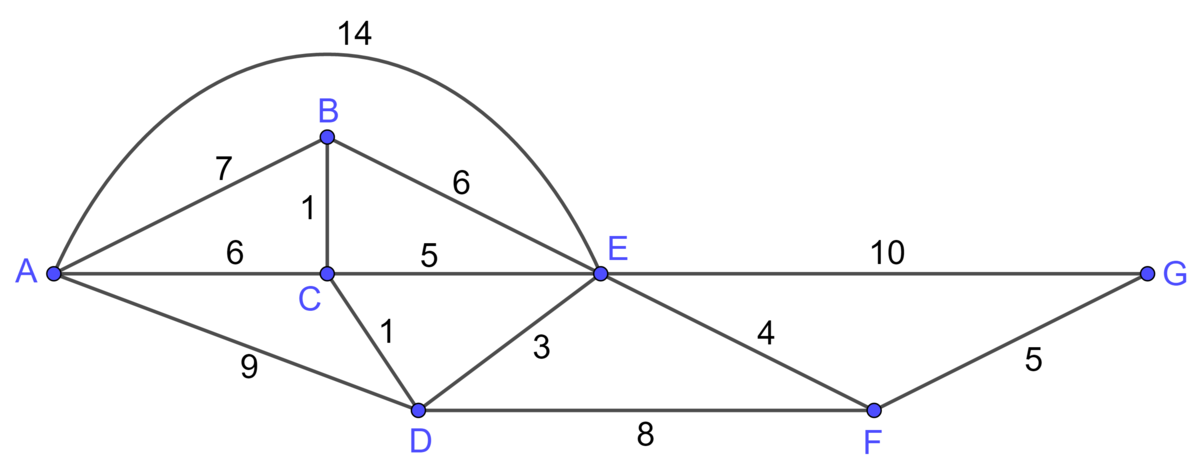
Solution

1. Assign each vertex that is adjacent to the starting vertex a letter and a number representing the previous vertex and the weight of the smallest path that connects them
   
   The vertex |A| is the starting point. The adjacent vertices are |B|, |C|, |D|, and |E|. We are looking for the path with the smallest value connecting each of these vertices to the starting vertex.
   
   For the vertex |B|, the path with the smallest value, |7|, is the path that starts directly from |A.| We therefore write |\color{red}{7(A)}| right next to the vertex |B.| For |C|, the path with the smallest value, |6|, comes directly from |A.| We write |\color{red}{6(A)}| right next to the vertex |C|. For |D|, the path coming directly from the vertex |A| has a value of |9|, but the one passing through the vertex |C| has a smaller value, i.e. |6+1=7|. We choose this last option by writing |\color{red}{7(C)}.| For |E|, the path with the smallest value is the one passing through |C| then through |D|, with a value of |6+1+3=10|. We write |\color{red}{10(D)}.|

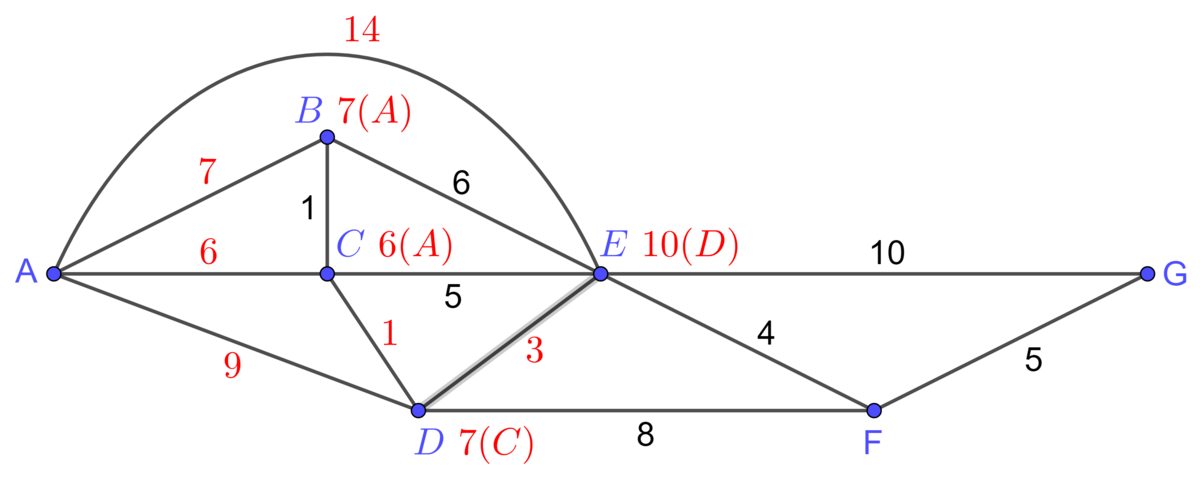
2. Repeat the first step until the final vertex is reached
   
   Since we already evaluated the vertices |B|, |C|, |D|, |E|, we now have to apply the same procedure to the adjacent vertices |F| and |G|.
   
   For |F|, the path coming from |D| has a value of |7+8=15| and the path coming from |E| has a value of |10+4=14.| So we choose the path starting from the vertex |E| by writing |\color{red}{14(E)}| next to |F.| For |G|, working in the same way, we find that the path of minimal value is the one starting from the vertex |F|, with a value of |14+5=19.| We write |\color{red}{19(F)}.|

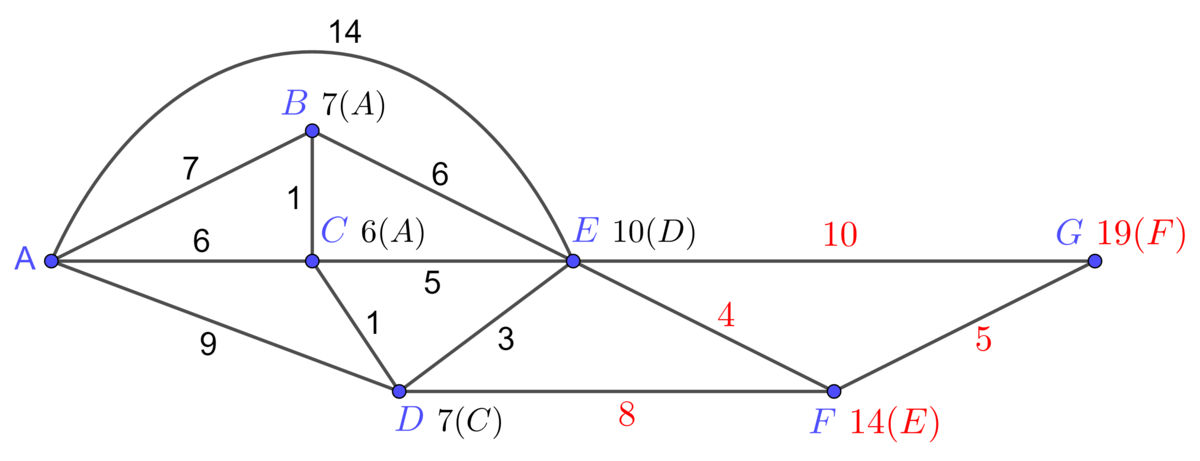
3. Work backwards to recreate the shortest path, moving from the last vertex to the starting vertex
   
   Starting from the last vertex, |G|, we follow the letters written next to each vertex to recreate the path of minimum value up to the starting vertex.

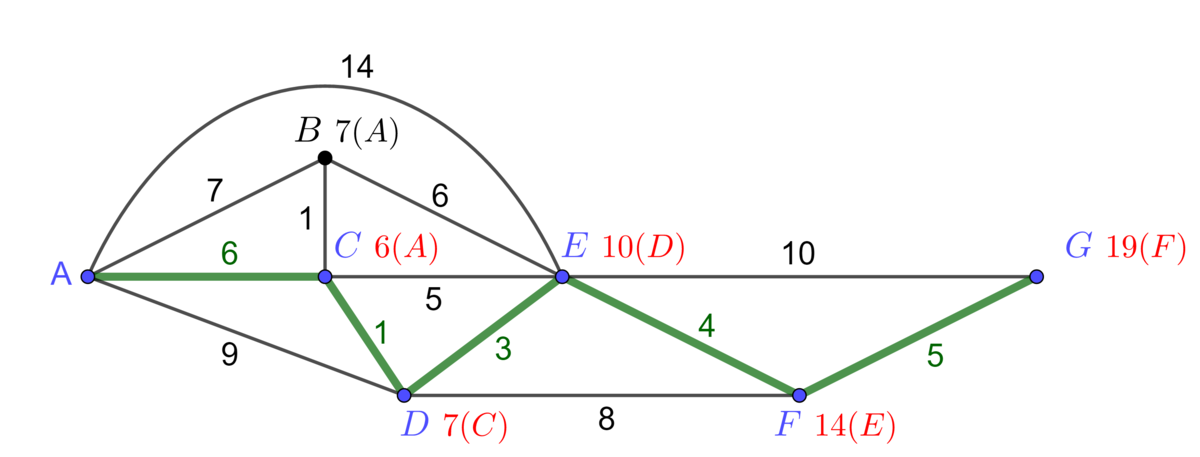
The path of minimum value is |A-C-D-E-F-G|. This is the route Laurie should take to get to Jessica's place as quickly as possible. She should be there in |19| minutes.