Un cercle est une courbe dont tous les points sont situés à égale distance d'un même point qu'on appelle le centre.
Comme toute figure plane, le cercle est affecté d'une aire et d'un périmètre. Par contre, dû à sa forme particulière, le moyen utilisé pour calculer ces grandeurs est différent des autres figures planes comme le carré, le rectangle ou le triangle.
Il est à noter que, lorsqu'il est question de l'aire d'un cercle, nous devons alors utiliser le terme « disque » afin de qualifier le cercle.
La circonférence d'un cercle correspond à la mesure de son contour, donc de son périmètre.
Pour mesurer la valeur de la circonférence d'un cercle, il est possible d'utiliser une corde et d'en faire le tour. Il suffit ensuite de mesurer la distance de l'enroulement de la corde à l'aide d'une règle. Par contre, une manière plus efficace de mesurer la circonférence d'un cercle est d'utiliser la formule suivante :
Avec le diamètre||\text{Circonférence}=3{,}1416\ldots\times\text{Diamètre}\\[10pt]C=\pi d||Avec le rayon||\text{Circonférence}=2\times3{,}1416\ldots\times\text{Rayon}\\[10pt]C=2\pi r||
On peut connaitre la mesure du diamètre à partir du rayon et vice versa. Puisque la valeur du diamètre équivaut à deux fois celle du rayon, il suffit donc de multiplier le rayon par deux.||\text{Diamètre}=2\times\text{Rayon}\\[10pt]d=2r||À l'inverse, il est possible d'obtenir la valeur du rayon en divisant le diamètre par deux.||\text{Rayon}=\text{Diamètre}\div2\\[10pt]r=\dfrac{d}{2}||
Le symbole |\pi| se lit « pi » et correspond à une valeur d'environ |\boldsymbol{3{,}1416}| arrondi au dix-millième près. Il s'agit d'un nombre irrationnel qui correspond au rapport entre la circonférence d'un cercle et son diamètre.||\pi=\dfrac{\text{Circonférence}}{\text{Diamètre}}\approx3{,}1416\ldots\\[10pt]\pi=\dfrac{C}{d}||Il est à noter que peu importe les dimensions du cercle, le rapport entre sa circonférence et son diamètre demeure toujours le même |(\pi| ou environ |3{,}1416).|
Quelle est la circonférence du cercle ci-dessous?
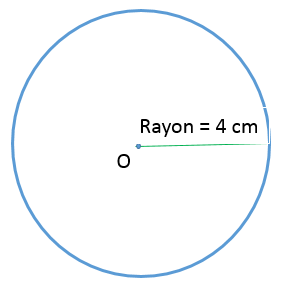
||\begin{align}C&=2\pi r\\[2pt]&\approx2\times3{,}1416\times4\\[2pt]&\approx25{,}13\end{align}||
La circonférence de ce cercle est de 25,13 cm.
Quelle est la circonférence du cercle ci-dessous?
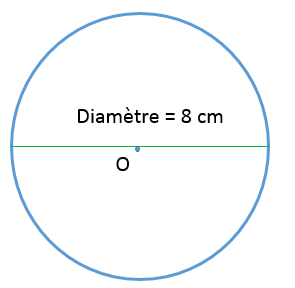
||\begin{align}C&=\pi d\\[2pt]&\approx3{,}1416\times8\\[2pt]&\approx25{,}13\end{align}||
La circonférence de ce cercle est de 25,13 cm.
Nous pouvons également isoler le rayon à partir de la circonférence d'un cercle. Par exemple, si la circonférence du cercle ci-dessous est de 15,71 cm, quel est son rayon?
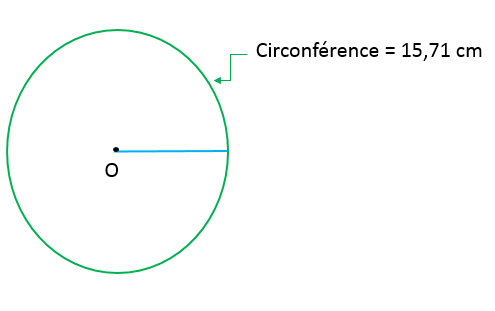
Dans ce cas, il s'agit d'utiliser la formule associée à la donnée recherchée (rayon) et de procéder à l'isolation de la variable.
||\begin{align}C&=2\pi r\\[2pt]15{,}71&=2\pi r\\[2pt]\color{#ec0000}{\dfrac{\color{black}{15{,}71}}{\boldsymbol{2}}}&=\color{#ec0000}{\dfrac{\color{black}{2\pi r}}{\boldsymbol{2}}}\\[2pt]7{,}855 &=\pi r\\[2pt]\color{#ec0000}{\dfrac{\color{black}{7{,}855}}{\boldsymbol{\pi}}}&=\color{#ec0000}{\dfrac{\color{black}{\pi r}}{\boldsymbol{\pi}}}\\[2pt]\dfrac{7{,}855}{\boldsymbol{3{,}1416}}&\approx r\\[2pt]2{,}5&\approx r\end{align}||Le rayon de ce cercle est de 2,5 cm.
L'aire d'un disque correspond à la surface qu'il occupe.
Contrairement à la circonférence, il est pratiquement impossible de connaitre l'aire d'un disque sans utiliser de formule. L'aire peut être calculée uniquement à partir de la valeur du rayon du disque.
||\text{Aire}=3{,}1416\ldots\times\text{Rayon}^2\\[10pt]A=\pi r^2||
Quelle est l'aire d'un disque dont le rayon vaut 6 cm?
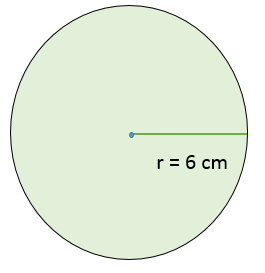
||\begin{align}A&=\pi r^2\\[2pt]&\approx3{,}1416\times6^2\\[2pt]&\approx3{,}1416\times36\\[2pt]&\approx113{,}09\end{align}||
L’aire de ce cercle est de 113,09 cm2.
Il est également possible d'isoler le rayon à partir de l'aire d'un disque. Par exemple, si un disque a une aire de 153,94 cm2, quel est son rayon?
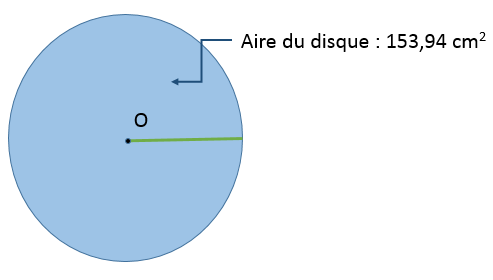
||\begin{align}A&=\pi r^2\\[2pt]153{,}94&=\pi r^2\\[2pt]\color{#ec0000}{\dfrac{\color{black}{153{,}94}}{\boldsymbol{\pi}}}&=\color{#ec0000}{\dfrac{\color{black}{\pi r^2}}{\boldsymbol{\pi}}}\\[2pt]\dfrac{153{,}94}{\boldsymbol{3{,}1416}}&\approx r^2\\[2pt]
49&\approx r^2\\[2pt]\color{#ec0000}{\sqrt{\color{black}{49}}}&\approx\color{#ec0000}{\sqrt{\color{black}{r^2}}}\\[2pt]7&\approx r\end{align}||
Le rayon de ce cercle est de 7 cm.
Il est possible de trouver l'aire d'un disque à partir de sa circonférence. D'abord, il est nécessaire de trouver le rayon. Par exemple, quelle est l'aire d'un cercle dont la circonférence est de 15,71 cm?
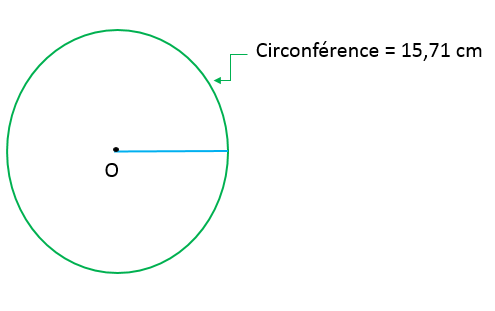
||\begin{align}C&=2\pi r\\[2pt]15{,}71&=2\pi r\\[2pt]\color{#ec0000}{\dfrac{\color{black}{15{,}71}}{\boldsymbol{2}}}&=\color{#ec0000}{\dfrac{\color{black}{2\pi r}}{\boldsymbol{2}}}\\[2pt]7{,}855 &=\pi r\\[2pt]\color{#ec0000}{\dfrac{\color{black}{7{,}855}}{\boldsymbol{\pi}}}&=\color{#ec0000}{\dfrac{\color{black}{\pi r}}{\boldsymbol{\pi}}}\\[2pt]\dfrac{7{,}855}{\boldsymbol{3{,}1416}}&\approx r\\[2pt]2{,}5&\approx r\end{align}||
||\begin{align}A&=\pi r^2\\[2pt]&\approx3{,}1416\times2{,}5^2\\[2pt]&\approx3{,}1416\times6{,}25\\[2pt]&\approx19{,}63\end{align}||L’aire de ce cercle est de 19,63 cm2.
