A circle is a curve whereby all the points are located at an equal distance from the same point, called the centre.
Like any plane figure, a circle has an area and a perimeter. However, due to its particular shape, how these quantities are calculated is different from other plane figures such as squares, rectangles, or triangles.
The circumference of a circle corresponds to the measure of its contour, i.e., its perimeter.
To measure the circumference of a circle, a rope can be wrapped around it. Then, simply measure the length of the uncoiled rope using a ruler. However, a more efficient way to measure the circumference of a circle is with the following formula:
With the diameter||\text{Circumference}=3.1416\ldots\times\text{Diameter}\\[10pt]C=\pi d||With the radius||\text{Circumference}=2\times3.1416\ldots\times\text{Radius}\\[10pt]C=2\pi r||
The measurement of the diameter can be determined from the radius and vice versa. Since the value of the diameter is twice that of the radius, simply multiply the radius by two.||\text{Diameter}=2\times\text{Radius}\\[10pt]d=2r||In reverse, it is possible to obtain the value of the radius by dividing the diameter by two.||\text{Radius}=\text{Diameter}\div2\\[10pt]r=\dfrac{d}{2}||
The symbol |\pi| means "pi" and has a value of approximately |\boldsymbol{3.1416}| rounded to the nearest ten-thousandth. It is an irrational number which corresponds to the ratio between a circle’s circumference and diameter.||\pi=\dfrac{\text{Circumference}}{\text{Diameter}}\approx3.1416\ldots\\[10pt]\pi=\dfrac{C}{d}||Note that regardless of the circle’s dimensions, the ratio between its circumference and its diameter is always the same |(\pi| or around |3.1416).|
What is the circumference of the following circle?
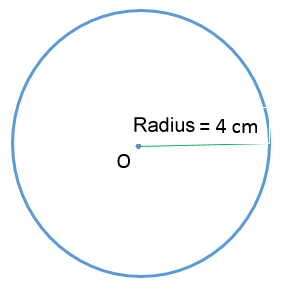
||\begin{align}C&=2\pi r\\[2pt]&\approx2\times3.1416\times4\\[2pt]&\approx25.13\end{align}||
The circumference of the circle is 25.13 cm.
What is the circumference of the following circle?
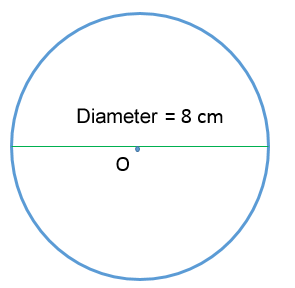
||\begin{align}C&=\pi d\\[2pt]&\approx3.1416\times8\\[2pt]&\approx25.13\end{align}||
The circumference of the circle is 25.13 cm.
The radius can also be found from the circumference of a circle. For example, if the circumference of the following circle is |15.71\ \text{cm}|, what is its radius?
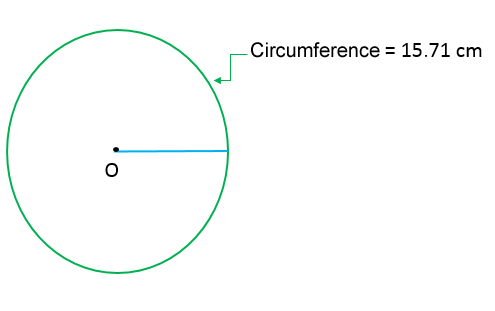
Here, use the formula associated with the number sought (radius) and then isolating the variable |r|.
||\begin{align}C&=2\pi r\\[2pt]15.71&=2\pi r\\[2pt]\color{#ec0000}{\dfrac{\color{black}{15.71}}{\boldsymbol{2}}}&=\color{#ec0000}{\dfrac{\color{black}{2\pi r}}{\boldsymbol{2}}}\\[2pt]7.855 &=\pi r\\[2pt]\color{#ec0000}{\dfrac{\color{black}{7.855}}{\boldsymbol{\pi}}}&=\color{#ec0000}{\dfrac{\color{black}{\pi r}}{\boldsymbol{\pi}}}\\[2pt]\dfrac{7.855}{\boldsymbol{3.1416}}&\approx r\\[2pt]2.5&\approx r\end{align}||The radius of the circle is 2.5 cm.
The area of a circle is its surface area.
Unlike the circumference, it is almost impossible to know the area of a circle without using a formula. The area can be calculated using only the value of the circle’s radius.
||\text{Area}=3.1416\ldots\times\text{Radius}^2\\[10pt]A=\pi r^2||
What is the area of a circle with a radius of |6\ \text{cm}|?
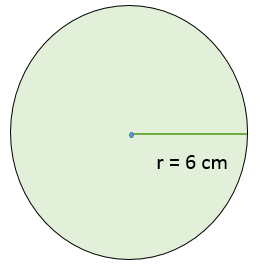
||\begin{align}A&=\pi r^2\\[2pt]&\approx3.1416\times6^2\\[2pt]&\approx3.1416\times36\\[2pt]&\approx113.09\end{align}||
The area of the circle is 114.09 cm2.
The radius can also be isolated from the area of a circle. For example, if a circle has an area of |153.94\ \text{cm}^2|, what is its radius’ measure?
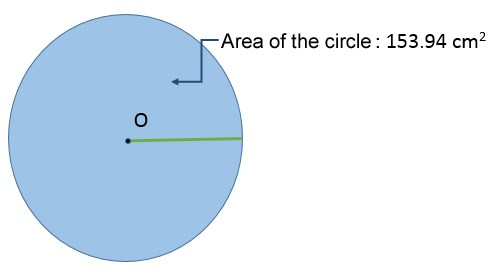
||\begin{align}A&=\pi r^2\\[2pt]153.94&=\pi r^2\\[2pt]\color{#ec0000}{\dfrac{\color{black}{153.94}}{\boldsymbol{\pi}}}&=\color{#ec0000}{\dfrac{\color{black}{\pi r^2}}{\boldsymbol{\pi}}}\\[2pt]\dfrac{153.94}{\boldsymbol{3.1416}}&\approx r^2\\[2pt]
49&\approx r^2\\[2pt]\color{#ec0000}{\sqrt{\color{black}{49}}}&\approx\color{#ec0000}{\sqrt{\color{black}{r^2}}}\\[2pt]7&\approx r\end{align}||
The radius of this circle is 7 cm.
The area of a circle can be found from its circumference. First, it is necessary to find the radius. For example, what is the area of a circle with a circumference of |15.71\ \text{cm}|?
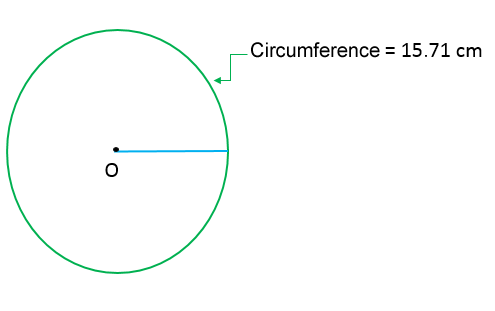
||\begin{align}C&=2\pi r\\[2pt]15.71&=2\pi r\\[2pt]\color{#ec0000}{\dfrac{\color{black}{15.71}}{\boldsymbol{2}}}&=\color{#ec0000}{\dfrac{\color{black}{2\pi r}}{\boldsymbol{2}}}\\[2pt]7.855 &=\pi r\\[2pt]\color{#ec0000}{\dfrac{\color{black}{7.855}}{\boldsymbol{\pi}}}&=\color{#ec0000}{\dfrac{\color{black}{\pi r}}{\boldsymbol{\pi}}}\\[2pt]\dfrac{7.855}{\boldsymbol{3.1416}}&\approx r\\[2pt]2.5&\approx r\end{align}||
||\begin{align}A&=\pi r^2\\[2pt]&\approx3.1416\times2.5^2\\[2pt]&\approx3.1416\times6.25\\[2pt]&\approx19.63\end{align}||The area of the circle is 19.63 cm2.
To confirm that you understand the area and perimeter of plane figures, see the following interactive Crash Course:
