La construction d'un losange ou d'un parallélogramme requiert l'utilisation d'outils de construction comme la règle, l'équerre, le rapporteur d'angles ou le compas. Puisque ces deux figures possèdent des propriétés différentes, leurs méthodes de construction respectives diffèrent également.
Un losange est un quadrilatère qui possède 4 côtés de même mesure, des côtés opposés paralléles et des angles opposés isométriques.
Pour dessiner un losange à l'aide de l'équerre et de la règle, il faut suivre les étapes suivantes:
- À l'aide de la règle, dessiner un segment dont la longueur correspond à la mesure de la grande diagonale.
- À l'aide d'une règle, trace le point qui se situe au milieu du segment. (Pour repérer ce point, on divise la mesure du segment par 2).
- À l'aide d'une équerre, tracer un segment perpendiculaire à partir du point milieu représenté sur le segment. Ce trait doit être plus long que la moitié de la petite diagonale.
- Effectuer la même procédure qu'à l'étape 3, mais de l'autre côté de la grande diagonale.
- À l'aide de la règle, indiquer l'emplacement qui correspond à la moitié de la petite diagonale sur chaque trait tracé aux étape 3 et 4.
- À l'aide de la règle, relier par des segments les marques à chaque extrémité de la grande diagonale.
Concrètement, on peut procéder de la façon suivante.
Supposons que l'on veuille représenter un losange dont la grande diagonale mesure |7\ \text{cm}| et la petite diagonale |4\ \text{cm}|, on peut suivre les étapes suivantes:
|
1. À l'aide de la règle, tracer un segment dont la longueur correspond à la grande base (7 cm).
|
2. À l'aide d'une règle, trace le point qui se situe au milieu du segment. (Pour repérer ce point, on divise la mesure du segment par 2). |
|
3. À l'aide d'une équerre, tracer un trait perpendiculaire à partir du point milieu représenté sur le segment. Ce trait doit être plus long que la moitié de la petite diagonale.
|
4. Effectuer la même procédure qu'à l'étape 3, mais de l'autre côté de la grande diagonale. |
|
5. À l'aide de la règle, indiquer l'emplacement qui correspond à la moitié de la petite diagonale sur chaque trait tracé aux étape 3 et 4 (2 cm).
|
6. À l'aide de la règle, relier par des segments les marques à chaque extrémité de la grande diagonale. |
Il est possible de dessiner un losange à l'aide de la règle et d'un rapporteur d'angles lorsque la mesure des côtés et la valeur des angles sont données.
-
À l'aide de la règle, tracer un segment dont la longueur correspond à la mesure d'un des côtés du losange.
-
Placer le rapporteur d'angles à l'une des extrémités du segment et construire l'angle selon la mesure désirée.
-
Placer le rapporteur d'angle à l'autre extrémités du segment initial et construire l'autre angle selon la mesure désirée.
-
En respectant les angles construits aux étapes 3 et 4, tracer deux segments dont la longueur correspond à la mesure des côtés du losange.
-
À l'aide de la règle, relier les extrémité des segments tracés à l'étape 4.
Concrètement, on peut arriver au résultat final en procédant de la façon suivante.
Trace un losange dont les côtés mesurent |6\ \text{cm}| et les angles mesurent respectivement |60^o| et |120^o|.
|
1. À l'aide de la règle, tracer un segment dont la longueur correspond à 6 cm. |
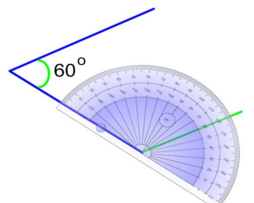
2. Placer le rapporteur d'angles à l'une des extrémités du segment et construire l'angle de 60o. |
|
3. Placer le rapporteur d'angle à l'autre extrémité du segment initial et construire l'angle de 120o.
|
4. En respectant les angles construits aux étapes 3 et 4, tracer deux segments dont la longueur correspond à 6 cm.
|
|
5. À l'aide de la règle, relier l'extrémité des segments tracés à l'étape 4. |
Un parallélogramme est un quadrilatère qui possède des côtés opposés isométriques et parallèles avec des angles opposés isométriques.
Pour construire un parallélogramme à l'aide du compas et d'une règle, il faut connaître les mesures des côtés.
- À l'aide de la règle, dessiner un segment horizontal correspondant à la longueur du grand côté du parallélogramme.
- À partir d'une extrémité du segment, tracer un segment dont la longueur correspond à la valeur du petit côté du parallélogramme. Faire attention de construire ce trait oblique.
- Ouvrir le compas selon la mesure du grand segment et placer la pointe sèche sur l'extrémité du segment oblique.
- Tracer un arc de cercle en direction du segment adjacent.
- Ouvrir le compas selon la mesure du petit segment oblique et placer la pointe sèche sur l'extrémité du segment initial.
- Tracer un arc de cercle en direction du segment adjacent en croisant le premier arc de cercle.
- À l'aide de la règle, relier les extrémités des deux segments au point de rencontre des deux arcs de cercle.
Concrètement, la construction d'un parallélogramme ressemble à l'exemple suivant.
Dessine un parallélogramme dont les grands côtés mesurent |8\ \text{cm}| et les petits côtés mesurent |3\ \text{cm}|.
|
1. À l'aide de la règle, dessiner un segment horizontal correspondant à la longueur du grand côté du parallélogramme (8 cm). |
2. À partir d'une extrémité du segment, tracer un segment dont la longueur correspond à la valeur du petit côté du parallélogramme (3 cm). Faire attention de construire ce trait oblique. |
|
3. Ouvrir le compas selon la mesure du |
4. Tracer un arc de cercle en |
|
5. Ouvrir le compas selon la mesure du |
6. Tracer un arc de cercle |
|
7. À l'aide de la règle, relier les extrémités des deux segments au point de rencontre des deux arcs de cercle.
|
|
Malgré la précision du parallélisme entre les côtés opposés, cette méthode ne tient pas compte de deux mesures assez importantes.
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><ol>
<li><span>Dans le cas où la <strong>mesure d'un angle</strong> serait donnée, on devrait utiliser un rapporteur d'angles pour s'assurer de la justesse de l'ouverture de chaque angle.</span></li>
<li><span>Dans le cas où la <strong>mesure de la hauteur et la mesure d'un angle</strong> sont données, on doit utiliser une notion un peu plus avancée en géométrie, soit <a href="/fr/eleves/bv/mathematiques/les-rapports-trigonometriques-dans-le-triangle-re-m1287">les rapports trigonométriques dans un triangle rectangle</a>. </span></li>
</ol>
</body></html>
Pour construire un parallélogramme à l'aide du rapporteur d'angles et d'une règle, il faut connaître les mesures des côtés et des angles.
- À l'aide de la règle, dessiner un segment horizontal dont la mesure correspond à celle du grand côté du parallélogramme.
- À l'aide du rapporteur d'angles, construire l'angle obtus du parallélogramme à l'une des extrémités du segment.
- À l'aide de la règle et en respectant l'angle construit à l'étape 2, tracer un segment dont la mesure correspond à celle du petit côté du parallélogramme.
- À l'aide du rapporteur d'angles, construire l'angle aigu du parallélogramme à l'autre extrémité du segment initial.
- À l'aide de la règle et en respectant l'angle construit à l'étape 4, tracer un segment dont la mesure correspond à celle du petit côté du parallélogramme.
- À l'aide de la règle, relier l'extrémité des segments obliques.
Concrètement, les étapes de construction sont représentées par les dessins suivants.
Trace un parallélogramme dont les bases mesurent |7\ \text{cm}|, les segments obliques mesurent |4\ \text{cm}| et dont les angles obtus et aigus mesurent respectivement |120^o| et |60^o|.
|
1. À l'aide de la règle, dessiner un segment horizontal dont la mesure correspond à celle du grand côté du parallélogramme (7 cm). |
2. À l'aide du rapporteur d'angles, construire l'angle obtus de 120o du parallélogramme à l'une des extrémités du segment. |
|
3. À l'aide de la règle et en respectant l'angle construit à l'étape 2, tracer un segment dont la mesure correspond à celle du petit côté du parallélogramme (4 cm). |
4. À l'aide du rapporteur d'angles, construire l'angle aigu de 60o du parallèlogramme à l'autre extrémité du segment initial. |
|
5. À l'aide de la règle et en respectant l'angle construit à l'étape 4, tracer un segment dont la mesure correspond à celle du petit côté du parallélogramme (4 cm). |
6. À l'aide de la règle, relier l'extrémité des segments obliques. |