La différence de deux carrés est un procédé qui permet de factoriser un polynôme de la forme |a^2 - b^2.|
Pour reconnaitre une différence de carrés, l'expression algébrique doit respecter les conditions suivantes :
1. Les deux termes doivent être des carrés.
2. Une soustraction doit relier les deux termes : |a^2\color{red}{-}b^2.|
Pour factoriser un binôme de la forme |a^2-b^2| à l'aide de la méthode de la différence de carrés, on doit :
1. Extrair les racines carrés des deux termes. ||\begin{align}\sqrt{a^2}&=\color{blue} {a}\\\sqrt{b^2}&= \color{green} {b}\end{align}||2. Appliquer l'identité remarquable suivante :||a^2-b^2=(\color{blue}{a}+\color{green}{b})(\color{blue}{a}-\color{green}{b})||
Soit l'expression |9x^20-16.|
1. Extraire les racines carrés des deux termes. ||\color{blue}{a}=\sqrt{a^2}=\sqrt{9x^2}=\color{blue} {3x}\\\color{green} {b}=\sqrt{b^2}=\sqrt{16}=\color{green} {4}||2. Appliquer l'identité remarquable. ||\begin{align}a^2-b^2&=(\color{blue}{a}+\color{green}{b})(\color{blue}{a}-\color{green}{b})\\&=(\color{blue}{3x}+\color{green}{4})(\color{blue}{3x}-\color{green}{4})\end{align}||La réponse obtenue est donc |(3x + 4) (3x – 4).|
Soit l'expression |36x^{4}y^2 - 9z^6.|
1. Extraire les racines carrés des deux termes. ||\color{blue}{a}=\sqrt{a^2}=\sqrt{36x^4y^2}=\color{blue} {6x^2y}\\\color{green}{b}=\sqrt{b^2}=\sqrt{9z^6}=\color{green} {3z^3}||2. Appliquer l'identité remarquable. ||\begin{align}a^2-b^2&=(\color{blue}{a}+\color{green}{b})(\color{blue}{a}-\color{green}{b})\\&=(\color{blue}{6x^2y}+\color{green}{3z^3})(\color{blue}{6x^2y}-\color{green}{3z^3})\end{align}||Lorsque l'on factorise un polynôme, on s'assure généralement qu'il le soit jusqu'à sa forme la plus complète. Ici, on peut poursuivre la factorisation avec une mise en évidence simple pour chaque parenthèse.
Mettre en évidence le facteur |3| pour chaque parenthèse : ||\begin{align}(6x^2y+3z^3)(6x^2y-3z^3)&=\color{red}{3}(2x^2y+z^3)\times\color{red}{3}(2x^2y-z^3)\\&=\color{red}{9}(2x^2y+z^3)(2x^2y-z^3)\end{align}||On obtient donc |9 (2x^{2}y + z^3) (2x^{2}y - z^3).|
Regardons un exemple différent : |9x^2 - 5.|
1. Extraire les racines carrés des deux termes.
Bien que |5| ne soit pas un carré parfait, on peut l'écrire sous la forme d'une racine comme ceci : |\sqrt{5}.| ||\color{blue}{a}=\sqrt{a^2}=\sqrt{9x^2}=\color{blue}{3x}\\\color{green} {b}=\sqrt{b^2}=\sqrt{5}=\color{green} {\sqrt{5}}|| 2. Appliquer l'identité remarquable. ||\begin{align}a^2-b^2&=(\color{blue}{a}+\color{green}{b})(\color{blue}{a}-\color{green}{b})\\&=(\color{blue}{3x}+\color{green}{\sqrt{5}})(\color{blue}{3x}-\color{green}{\sqrt{5}})\end{align}||Ainsi, on obtient |(3x+ \sqrt{5})(3x- \sqrt{5}).|
Les facteurs d'une différence de carrés sont toujours deux binômes conjugués, c'est-à-dire que l'un est la somme de deux termes et l'autre, la différence des deux mêmes termes.
Voici la démonstration géométrique de l'identité remarquable |a^2-b^2=(a+b)(a-b).|
1) On commence par un grand carré dont le côté mesure |a.| L'aire de ce carré est |a^2| puis on enlève un petit carré dont le côté mesure |b| et qui a donc une aire de |b^2.|
L'aire de la partie colorée est donc : |\color{red}{\text{Aire}}=a^2-b^2.|
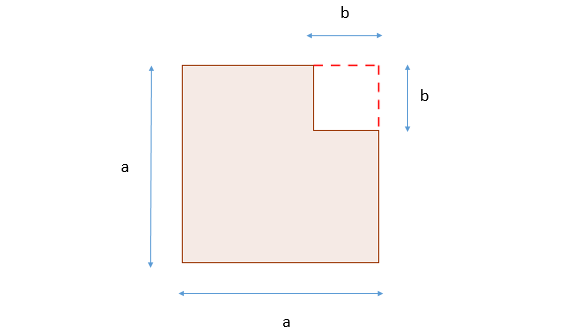
2) On ajoute une ligne verticale pour séparer le polygone coloré en deux rectangles.
L'aire du polygone devient : |\color{red}{\text{Aire}}=a^2-b^2=a(a-b)+b(a-b).|
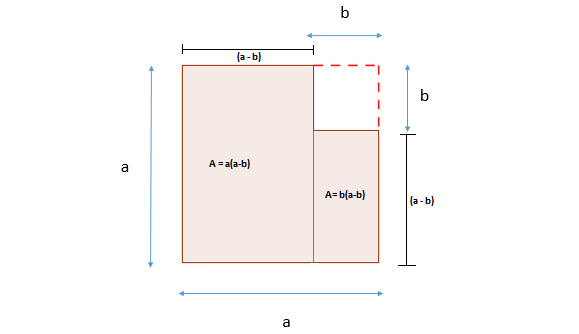
3) Il ne reste plus qu'à faire une mise en évidence simple pour obtenir l'identité remarquable.||\begin{align}\color{red}{\text{Aire}}=a^2-b^2&=a(a-b)+b(a-b)\\a^2-b^2&=(a+b)(a-b)\end{align}||