The Difference of Squares

Finding a difference of squares is a technique used to factor a polynomial of the form |a^2 - b^2.|

To recognize a difference of squares, the algebraic expression must respect the following conditions.

1. Both terms must be squares.

2. A subtraction must connect the two terms: |a^2\color{red} {-}b^2.|

To factor a binomial of the form |a^2-b^2| using the difference of squares technique, follow these steps.

1. Find the square roots of the two terms. ||\begin{align}\sqrt{a^2}&=\color{blue} {a}\\\sqrt{b^2}&= \color{green} {b}\end{align}|| 

2. Apply the identity of squares. ||a^2-b^2=(\color{blue}{a}+\color{green}{b})(\color{blue}{a}-\color{green}{b})||

Consider the expression |9x^2– 16.|

1. Find the square roots of the two terms ||\color{blue}{a}=\sqrt{a^2}=\sqrt{9x^2}=\color{blue} {3x}\\\color{green} {b}=\sqrt{b^2}=\sqrt{16}=\color{green} {4}||

2. Apply the identity of squares ||\begin{align}a^2-b^2&=(\color{blue}{a}+\color{green}{b})(\color{blue}{a}-\color{green}{b})\\&=(\color{blue}{3x}+\color{green}{4})(\color{blue}{3x}-\color{green}{4})\end{align}||The answer obtained is |(3x + 4) (3x – 4).|

Consider the expression |36x^{4}y^2 - 9z^6.|

1. Find the square roots of the two terms ||\color{blue}{a}=\sqrt{a^2}=\sqrt{36x^4y^2}=\color{blue} {6x^2y}\\\color{green}{b}=\sqrt{b^2}=\sqrt{9z^6}=\color{green} {3z^3}||

2. Apply the identity of squares ||\begin{align}a^2-b^2&=(\color{blue}{a}+\color{green}{b})(\color{blue}{a}-\color{green}{b})\\&=(\color{blue}{6x^2y}+\color{green}{3z^3})(\color{blue}{6x^2y}-\color{green}{3z^3})\end{align}|| When factoring a polynomial, make sure it is factored to its most complete form. So here, continue the factoring process by factoring out the common factor from each term in brackets. 
   
   Take out the factor |3| from each term in parentheses. ||\begin{align}(6x^2y+3z^3)(6x^2y-3z^3)&=\color{red}{3}(2x^2y+z^3)\cdot \color{red}{3}(2x^2y-z^3)\\&=\color{red}{9}(2x^2y+z^3)(2x^2y-z^3)\end{align}||The answer is |9 (2x^{2}y + z^3) (2x^{2}y - z^3).|

Let's look at a different example: |9x^2 - 5.|

1. Find the square roots of the two terms
   
   Although |5| is not a perfect square, write it as a root, as follows: |\sqrt{5}.| ||\color{blue}{a}=\sqrt{a^2}=\sqrt{9x^2}=\color{blue}{3x}\\\color{green} {b}=\sqrt{b^2}=\sqrt{5}=\color{green} {\sqrt{5}}||

2. Apply the identity of squares ||\begin{align}a^2-b^2&=(\color{blue}{a}+\color{green}{b})(\color{blue}{a}-\color{green}{b})\\&=(\color{blue}{3x}+\color{green}{\sqrt{5}})(\color{blue}{3x}-\color{green}{\sqrt{5}})\end{align}|| The answer obtained is |(3x+ \sqrt{5})(3x- \sqrt{5}).|

The factors of a difference of squares are always two conjugate binomials, that is, one is the sum of two terms and the other is the difference of the same two terms.

The following is the geometric representation of the identity of squares: |a^2-b^2=(a+b)(a-b).|

1. Start with a large square whose side measures |a|. The area of the square is |a^2|. Then, remove a smaller square with sides of length |b| and an area of |b^2.|
   
   The area of the colored part will then equal the following: |\color{red}{Area}=a^2-b^2.|

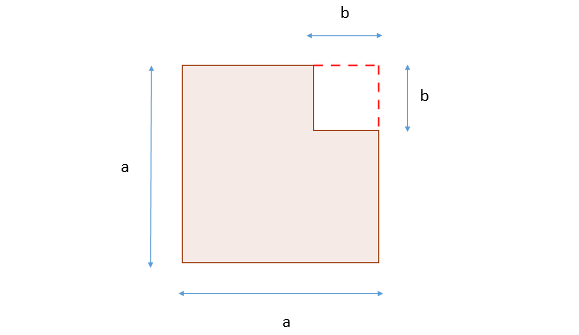
2. Add a vertical line to separate the colored polygon into two rectangles.
   
   The area of the polygon becomes |\color{red}{Area}=a^2-b^2=a(a-b)+b(a-b).|

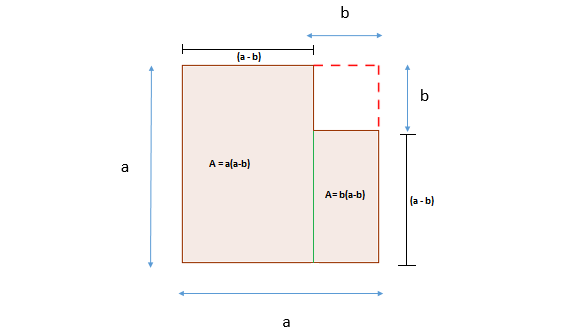
3. Finally, factor out the common factor to obtain the identity of squares. ||\begin{align}\color{red}{Area}=a^2-b^2&=a(a-b)+b(a-b)\\a^2-b^2&=(a+b)(a-b)\end{align}||