La notation scientifique est une notation qui permet d'exprimer et de comparer facilement de très grands ou de très petits nombres. Comme l'indique son nom, cette notation est notamment utilisée en science pour exprimer des mesures. C'est pourquoi cette notation est généralement appliquée aux nombres positifs seulement.
La notation scientifique est composée de 2 facteurs.
-
Le 1er facteur, souvent appelé la mantisse, est un nombre décimal |(\color{#333fb1}{a})| supérieur ou égal à |1,| mais inférieur à |10| et formé des chiffres significatifs du nombre initial.
-
Le 2e facteur est une puissance de |10| exprimée en notation exponentielle qui indique l'ordre de grandeur du nombre.
-
L'exposant |\color{#3a9a38}{n}| est un nombre entier différent de zéro.
-
Si |\color{#3a9a38}{n}\geq1,| le nombre initial est plus grand que |1.|
-
Si |\color{#3a9a38}{n}\leq-1,| le nombre initial est compris entre |0| et |1.| ||\begin{align}\large&\boldsymbol{\color{#333fb1}{a}}\times \boldsymbol{\color{#3a9a38}{10^n}}\\[-3pt] &\!\!\!\!\!\!\boldsymbol{\color{#333fb1}{\nearrow}}\qquad\;\boldsymbol{\color{#3a9a38}{\nwarrow}}\\ \boldsymbol{\color{#333fb1}{1^\textbf{er}\ \textbf{facteur}}}&\qquad\ \ \boldsymbol{\color{#3a9a38}{2^\textbf{e}\ \textbf{facteur}}}\\ 1\leq \boldsymbol{\color{#333fb1}{a}}<10&\qquad\ \ \ \ \ \boldsymbol{\color{#3a9a38}{n}}\in\mathbb{Z}^*\end{align}||
-
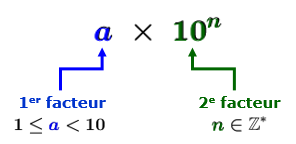
La distance entre la Lune et la Terre est de |384\ 400\:\text{km}.| En exprimant ce nombre en notation scientifique, on obtient ceci.||\boldsymbol{\color{#333fb1}{3{,}844}}\,\times\,\boldsymbol{\color{#3a9a38}{10^5}}\ \text{km}||
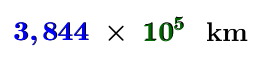
La masse de ce moustique est d'environ |0{,}000\, 001\, 07\ \text{kg}.| En exprimant ce nombre en notation scientifique, on obtient ceci.||\boldsymbol{\color{#333fb1}{1{,}07}}\,\times\,\boldsymbol{\color{#3a9a38}{10^{-6}}}\ \text{kg}||On remarque que le 1er facteur est un nombre décimal supérieur à |1| et inférieur à |10|. Il contient les chiffres significatifs du nombre initial.
Pour ce qui est du 2e facteur, il indique l'ordre de grandeur du nombre initial. Comme |10^{-6}=0{,}000\, 001,| ce facteur indique que le nombre initial est de l'ordre des millionièmes. En d'autres mots, on a ceci.||1{,}07\times 10^{-6}=1{,}07\times 0{,}000\, 001=0{,}000\, 001\, 07||
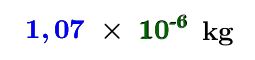
On remarque que le 1er facteur est un nombre décimal supérieur à |1| et inférieur à |10|. Il contient les chiffres significatifs du nombre initial.
Pour ce qui est du 2e facteur, il indique l'ordre de grandeur du nombre initial. Comme |10^{-6}=0{,}000\, 001,| ce facteur indique que le nombre initial est de l'ordre des millionièmes. En d'autres mots, on a ceci.||1{,}07\times 10^{-6}=1{,}07\times 0{,}000\, 001=0{,}000\, 001\, 07||
Deux cas sont possibles ici. Soit le nombre est exprimé en notation décimale, soit il est déjà exprimé comme un produit de 2 facteurs dont le 2e est une puissance de |10.| Nous présenterons une méthode pour chacun des cas.
-
Si le nombre initial n'a pas de virgule, ajouter une virgule à droite de la position des unités.
-
Déplacer la virgule par bonds vers la gauche ou vers la droite, jusqu'à l'obtention d'un nombre plus grand ou égal à |1,| mais plus petit que |10,| tout en comptant le nombre de bonds!
-
Écrire le nombre en notation scientifique.
|\small \bullet| Le 1er facteur correspond au nombre obtenu à l'étape 2 (Enlever les |0| inutiles)
|\small \bullet| Le 2e facteur correspond au nombre de bonds effectués à l'étape 2.
|\small \circ| Si les bonds ont été effectués vers la gauche, l'exposant sera positif.
|\small \circ| Si les bonds ont été effectués vers la droite, l'exposant sera négatif.
Exprime le nombre |85\:200| en notation scientifique.
-
Si le nombre initial n'a pas de virgule, ajouter une virgule à droite de la position des unités.
Comme le nombre initial est un nombre entier, il ne contient pas de virgule. On lui ajoute donc une virgule à droite de la position des unités, comme ceci.||85\,200\boldsymbol{\color{#EC0000}{,}}|| -
Déplacer la virgule par bonds vers la gauche ou vers la droite, jusqu'à l'obtention d'un nombre plus grand ou égal à |1,| mais plus petit que |10.| Compter le nombre de bonds.
Il faut déplacer la virgule vers la gauche.||\underset{\ \ \ \ 4\ \text{bonds}}{8\color{#ec0000}{\boldsymbol{,}\underleftarrow{\color{black}{\!5\ 200}}\boldsymbol{,}}}||Après |\boldsymbol{\color{#3a9a38}{4}}| bonds vers la gauche, on obtient le nombre |8{,}5200.| -
Écrire le nombre en notation scientifique.
Le 1er facteur correspond à |\boldsymbol{\color{#333fb1}{8{,}52}}.| On l'obtient en enlevant les zéros inutiles au nombre obtenu à l'étape 2. On remarque que ce nombre est compris entre |1| inclusivement et |10| exclusivement.Le 2e facteur correspond à |\boldsymbol{\color{#3a9a38}{10^4}}.| L'exposant correspond au nombre de bonds effectués à l'étape 2. Comme on a effectué les bonds vers la gauche, l'exposant est positif.
On obtient donc que la notation scientifique du nombre |85\ 200| est le suivant.||\boldsymbol{\color{#333fb1}{8{,}52}}\,\times\,\boldsymbol{\color{#3a9a38}{10^{4}}}||

2. Déplacer la virgule par bonds vers la gauche ou vers la droite, jusqu'à l'obtention d'un nombre plus grand ou égal à |1,| mais plus petit que |10.| Compter le nombre de bonds!
Il faut déplacer la virgule vers la gauche.
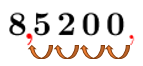
Après 4 bonds vers la gauche, on obtient le nombre |8{,}5200.|
3. Écrire le nombre en notation scientifique.
Le 1er facteur correspond à |\color{blue}{8{,}52}|. On l'obtient en enlevant les zéros inutile au nombre obtenu à l'étape 2. On remarque que ce nombre est compris entre |1| inclusivement et |10| exclusivement.
Le 2e facteur correspond à |\color{green}{10^4}|. L'exposant correspond au nombre de bonds effectués à l'étape 2. Comme on a effectué les bonds vers la gauche, l'exposant est positif.
On obtient donc que la notation scientifique du nombre |85\ 200| est :
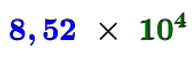
Exprime le nombre |0{,}000\,020\,56| en notation scientifique.
-
Si le nombre initial n'a pas de virgule, ajouter une virgule à droite de la position des unités.
Ce nombre contient déjà une virgule, on peut donc passer directement à l'étape 2.||0{\boldsymbol{\color{#EC0000}{,}}}000\,020\,56|| -
Déplacer la virgule par bonds vers la gauche ou vers la droite, jusqu'à l'obtention d'un nombre plus grand ou égal à |1,| mais plus petit que |10.| Compter le nombre de bonds.
Il faut déplacer la virgule vers la droite.||\underset{\!\!\!\!\!\!5\ \text{bonds}}{0\color{#ec0000}{\boldsymbol{,}\underrightarrow{\color{black}{\!000\,02}}{\boldsymbol{,}}\color{black}{0\,56}}}||Après |\boldsymbol{\color{#3a9a38}{5}}| bonds vers la droite, on obtient le nombre |2{,}056.| -
Écrire le nombre en notation scientifique
Le 1er facteur correspond à |\boldsymbol{\color{#333fb1}{2{,}056}}.| On remarque que ce nombre est compris entre |1| inclusivement et |10| exclusivement.Le 2e facteur correspond à |\boldsymbol{\color{#3a9a38}{10^{-5}}}.| L'exposant correspond au nombre de bonds effectués à l'étape 2. Comme on a fait les bonds vers la droite, l'exposant est négatif.
On obtient donc que la notation scientifique du nombre |0{,}000\,020\,56| est le suivant.||\boldsymbol{\color{#333fb1}{2{,}056}}\,\times\,\boldsymbol{\color{#3a9a38}{10^{-5}}}||

2. Déplacer la virgule par bonds vers la gauche ou vers la droite, jusqu'à l'obtention d'un nombre plus grand ou égal à |1,| mais plus petit que |10.| Compter le nombre de bonds!
Il faut déplacer la virgule vers la droite.
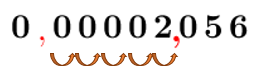
Après 5 bonds vers la droite, on obtient le nombre |2{,}056.|
3.Écrire le nombre en notation scientifique
Le 1erfacteur correspond à |\color{blue}{2{,}056}|. On remarque que ce nombre est compris entre |1| inclusivement et |10| exclusivement.
Le 2e facteur correspond à |\color{green}{10^{\text{-}5}}|. L'exposant correspond au nombre de bonds effectués à l'étape 2. Comme on a fait les bonds vers la droite, l'exposant est négatif.
On obtient donc que la notation scientifique du nombre |0{,}000\,020\,56| est :

Voici d'autres exemples.
||\begin{align}356\ 200&=3{,}562\times 10^5 & &\quad & 0{,}001\,3&=1{,}3\times 10^{-3}\\ \\ 404\ 000\ 000&=4{,}04\times 10^8 & &\quad & 0{,}000\,007&=7\times 10^{-6}\end{align}||
Dans certaines situations, le nombre à exprimer en notation scientifique peut déjà être écrit sous la forme d'un produit de facteurs, comme ceux-ci. ||0{,}03\ \times\ 10^{5}\qquad \qquad 432{,}4\ \times\ 10^{-10}||
On peut être porté à croire que ces nombres sont déjà exprimés en notation scientifique, mais attention! Le 1er facteur de ces nombres n'est pas compris entre |1| inclusivement et |10| exclusivement, c'est pourquoi ils ne sont pas exprimés en notation scientifique.
Voici une méthode permettant de remettre ces nombres en notation scientifique.
-
Transformer le 1er facteur en un nombre compris entre |1| inclusivement et |10| exclusivement en le multipliant ou en le divisant par la puissance de |10| adéquate.
-
Pour conserver la valeur du nombre, appliquer l'opération inverse au 2e facteur.
Si on a multiplié le 1er facteur par une puissance de |10,| on doit diviser le 2e facteur par cette même puissance.
Si on a divisé le 1er facteur par une puissance de |10,| on doit multiplier le 2e facteur par cette même puissance.
Exprime le nombre |356{,}2\ \times\ 10^7| en notation scientifique.
-
Transformer le 1er facteur en un nombre compris entre |\boldsymbol{1}| inclusivement et |\boldsymbol{10}| exclusivement en le multipliant ou en le divisant par la puissance de |\boldsymbol{10}| adéquate
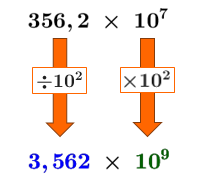
Le 1er facteur du nombre est |356{,}2.| Pour le transformer en nombre compris entre |1| inclusivement et |10| exclusivement, on doit le diviser par |100,| soit par |10^2.| On obtient donc ceci.||356{,}2\div 10^2=\color{#333fb1}{3{,}562}|| -
Appliquer l'opération inverse au 2e facteur
Pour conserver la valeur du nombre, on doit donc multiplier le 2e facteur par |10^2.| En utilisant les propriétés des exposants, on obtient que |10^7\times 10^2=10^{7+2}=\color{#3a9a38}{10^9}.| ||\large 356{,}2\,\times\,10^7\\ \downarrow\qquad\ \ \ \ \downarrow\\ \boxed{\div10^2}\quad\ \ \boxed{\times 10^2}\\ \downarrow\qquad\ \ \ \ \downarrow\\ \large \boldsymbol{\color{#333fb1}{3{,}562}}\,\times\,\boldsymbol{\color{#3a9a38}{10^9}}||
Exprime le nombre |0{,}121\ \times\ 10^{-14}| en notation scientifique.
-
Transformer le 1er facteur en un nombre compris entre |\boldsymbol{1}| inclusivement et |\boldsymbol{10}| exclusivement en le multipliant ou en le divisant par la puissance de |\boldsymbol{10}| adéquate
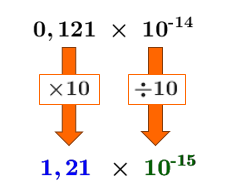
Le 1er facteur du nombre est |0{,}121.| Pour le transformer en nombre compris entre |1| inclusivement et |10| exclusivement, on doit le multiplier par |10,| soit par |10^1.| On obtient donc ceci.||0{,}121\times 10=\color{#333fb1}{1{,}21}|| -
Appliquer l'opération inverse au 2e facteur
Pour conserver la valeur du nombre, on doit donc diviser le 2e facteur par |10.| En utilisant les propriétés des exposants, on obtient que |10^{-14}\div 10=10^{-14-1}=\color{#3a9a38}{10^{-15}}.| ||\large 0{,}121\,\times\,10^{-14}\\ \downarrow\qquad\ \ \ \ \downarrow\\ \boxed{\times 10}\quad\ \ \boxed{\div 10}\\ \downarrow\qquad\ \ \ \ \downarrow\\ \large \boldsymbol{\color{#333fb1}{1{,}21}}\,\times\,\boldsymbol{\color{#3a9a38}{10^{-15}}}||
Pour additionner ou soustraire des nombres en notation scientifique, il faut premièrement les remettre sur le même ordre de grandeur. En d'autres mots, il faut les exprimer à l'aide de la même puissance de |10.| Voici une façon de procéder.
-
Identifier le nombre en notation scientifique ayant la plus grande puissance de |10.|
-
Exprimer l'autre nombre à l'aide de cette puissance de |10.|
-
Additionner ou soustraire les nombres en additionnant ou en soustrayant les 1ers facteurs seulement.
-
Exprimer le résultat en notation scientifique, au besoin.
Effectue l'opération suivante et exprime le résultat en notation scientifique.||5{,}6\times 10^5+4{,}42\times 10^7||
-
Identifier le nombre en notation scientifique ayant la plus grande puissance de |\boldsymbol{10}|
Le nombre ayant la puissance de |10| la plus grande est |4{,}42\times 10^7.| -
Exprimer l'autre nombre à l'aide de cette puissance de |\boldsymbol{10}|
On doit exprimer le nombre |5{,}6\times 10^5| à l'aide de la puissance |10^7.| On devra donc multiplier le 2e facteur de ce nombre par |10^2.| Pour conserver la valeur du nombre, on devra diviser le 1er facteur par |10^2.| ||\large 5{,}6\,\times\,10^{5}\\ \downarrow\qquad\ \ \ \ \downarrow\\ \boxed{\div 10^2}\quad\ \ \boxed{\times 10^2}\\ \downarrow\qquad\ \ \ \ \downarrow\\ \large 0{,}056\,\times\,10^{7}|| -
Additionner les nombres en additionnant les 1ers facteurs seulement
On peut maintenant effectuer l'opération.||\boldsymbol{\color{#333fb1}{0{,}056}}\times 10^7+\boldsymbol{\color{#333fb1}{4{,}42}}\times 10^7=\boldsymbol{\color{#333fb1}{4{,}476}}\times 10^7|| -
Exprimer le résultat en notation scientifique, au besoin
Comme le 1er facteur du résultat est compris entre |1| inclusivement et |10| exclusivement, il est déjà en notation scientifique. Il n'y a pas de changement à faire. La réponse est donc la suivante.||\boldsymbol{\color{#333fb1}{4{,}476}}\times \boldsymbol{\color{#3a9a38}{10^7}}||

3. Additionner les nombres en additionnant les 1er facteurs seulement.
On peut maintenant effectuer l'opération.
||\color{blue}{0,056}\times 10^7+\color{blue}{4,42}\times 10^7=\color{blue}{4,476}\times 10^7||
4. Exprimer le résultat en notation scientifique, au besoin.
Comme le 1er facteur du résultat est compris entre |\small 1| inclusivement et |\small 10| exclusivement, il est déjà en notation scientifique. Il n'y a pas de changement à faire. La réponse est donc: ||\color{blue}{4,476}\times \color{green}{10^7}||
Effectue l'opération suivante et exprime le résultat en notation scientifique. ||1{,}3\times 10^{-4}-7{,}9\times 10^{-5}||
-
Identifier le nombre en notation scientifique ayant la plus grande puissance de |\boldsymbol{10}|
Le nombre ayant la puissance de |10| la plus grande est |1{,}3\times 10^{-4}.| -
Exprimer l'autre nombre à l'aide de cette puissance de |\boldsymbol{10}|
On doit exprimer le nombre |7{,}9\times 10^{-5}| à l'aide de la puissance |10^{-4}.| On devra donc multiplier le 2e facteur de ce nombre par |10^1.| Pour conserver la valeur de ce nombre, on devra diviser le 1er facteur par |10^1.| ||\large 7{,}9\,\times\,10^{-5}\\ \downarrow\qquad\ \ \ \ \downarrow\\ \boxed{\div 10}\quad\ \ \boxed{\times 10}\\ \downarrow\qquad\ \ \ \ \downarrow\\ \large 0{,}79\,\times\,10^{-4}|| -
Soustraire les nombres en soustrayant les 1ers facteurs seulement
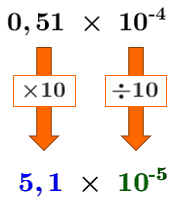
On peut maintenant effectuer l'opération.||\boldsymbol{\color{#333fb1}{1{,}3}}\times 10^{-4}-\boldsymbol{\color{#333fb1}{0{,}79}}\times 10^{-4}=\boldsymbol{\color{#333fb1}{0{,}51}}\times 10^{-4}|| -
Exprimer le résultat en notation scientifique, au besoin
Le 1er facteur n'est pas inclus entre |1| inclusivement et |10| exclusivement. On doit donc effectuer les changements suivants pour obtenir une réponse en notation scientifique.||\large 0{,}51\,\times\,10^{-4}\\ \downarrow\qquad\ \ \ \ \downarrow\\ \boxed{\times 10}\quad\ \ \boxed{\div 10}\\ \downarrow\qquad\ \ \ \ \downarrow\\ \large \boldsymbol{\color{#333fb1}{5{,}1}}\,\times\,\boldsymbol{\color{#3a9a38}{10^{-5}}}||
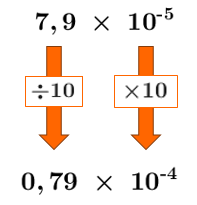
3. Soustraire les nombres en soustrayant les 1er facteurs seulement.
On peut maintenant effectuer l'opération.
||\color{blue}{1,3}\times 10^{\text{-}4}-\color{blue}{0,79}\times 10^{\text{-}4}=\color{blue}{0,51}\times 10^{\text{-}4}||
4. Exprimer le résultat en notation scientifique, au besoin.
Le 1er facteur n'est pas inclus entre |\small 1| inclusivement et |\small 10| exclusivement. On doit donc effectuer les changements suivants pour obtenir une réponse en notation scientifique.
Il existe quelques méthodes permettant de multiplier ou de diviser des nombres en notation scientifique. Nous en présenterons une.
-
Multiplier ou diviser les 1ers facteurs ensemble et les 2es facteurs ensemble.
-
Exprimer le résultat en notation scientifique, au besoin.
Effectue l'opération suivante et exprime ton résultat en notation scientifique. ||2{,}9\times 10^{15}\ \times \ 8{,}1\times 10^{-3}||
-
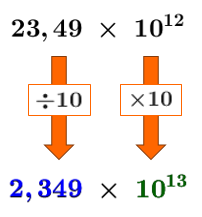
Multiplier les 1ers facteurs ensemble et les 2es facteurs ensemble||\begin{align}&\boldsymbol{\color{#333fb1}{2{,}9}}\times \boldsymbol{\color{#3a9a38}{10^{15}}} \times\, \boldsymbol{\color{#333fb1}{8{,}1}}\times \boldsymbol{\color{#3a9a38}{10^{-3}}}\\[5pt]=\, (&\boldsymbol{\color{#333fb1}{2{,}9}}\times\boldsymbol{\color{#333fb1}{8{,}1}})\ \times (\boldsymbol{\color{#3a9a38}{10^{15}}}\times \boldsymbol{\color{#3a9a38}{10^{-3}}})\\[5pt] =\ &\boldsymbol{\color{#333fb1}{23{,}49}} \times \boldsymbol{\color{#3a9a38}{10^{15-3}}}\\[5pt] =\ &\boldsymbol{\color{#333fb1}{23{,}49}}\times \boldsymbol{\color{#3a9a38}{10^{12}}} \end{align}||
-
Exprimer le résultat en notation scientifique, au besoin
Comme le 1er facteur du résultat n'est pas inclus entre |1| inclusivement et |10| exclusivement, on doit effectuer les changement suivants pour obtenir une réponse en notation scientifique.||\large 23{,}49\,\times\,10^{12}\\ \downarrow\qquad\ \ \ \ \downarrow\\ \boxed{\div 10}\quad\ \ \boxed{\times 10}\\ \downarrow\qquad\ \ \ \ \downarrow\\ \large \boldsymbol{\color{#333fb1}{2{,}349}}\,\times\,\boldsymbol{\color{#3a9a38}{10^{13}}}||
Effectue l'opération suivante et exprime ton résultat en notation scientifique. ||\dfrac{7{,}8\times 10^{-2}}{1{,}5\times 10^{-8}}||
-
Diviser les 1ers facteurs ensemble et les 2es facteurs ensemble||\begin{align}\dfrac{\boldsymbol{\color{#333fb1}{7{,}8}}\times \boldsymbol{\color{#3a9a38}{10^{-2}}}}{\boldsymbol{\color{#333fb1}{1{,}5}}\times \boldsymbol{\color{#3a9a38}{10^{-8}}}}&=\dfrac{\boldsymbol{\color{#333fb1}{7{,}8}}}{\boldsymbol{\color{#333fb1}{1{,}5}}} \times \dfrac{\boldsymbol{\color{#3a9a38}{10^{-2}}}}{\boldsymbol{\color{#3a9a38}{10^{-8}}}}\\[5pt] &=\,\boldsymbol{\color{#333fb1}{5{,}2}}\ \times\ \boldsymbol{\color{#3a9a38}{10^{-2-^-8}}}\\[5pt] &=\,\boldsymbol{\color{#333fb1}{5{,}2}}\ \times\ \boldsymbol{\color{#3a9a38}{10^6}}\end{align}||
-
Exprimer le résultat en notation scientifique, au besoin
Comme le 1er facteur du résultat est compris entre |1| inclusivement et |10| exclusivement, il est déjà en notation scientifique. Il n'y a pas de changement à faire. La réponse est donc la suivante.||\boldsymbol{\color{#333fb1}{5{,}2}}\ \times\ \boldsymbol{\color{#3a9a38}{10^6}}||
Afin de simplifier l'écriture de très grands ou de très petits nombres, le système international propose certains préfixes en lien avec la notation scientifique. En voici quelques-uns.
| Puissance de |\boldsymbol{10}| | Nombre | Préfixe | Symbole |
|---|---|---|---|
| |10^{12}| | |1\,000\,000\,000\,000| | Téra | |\text{T}| |
| |10^9| | |1\, 000\, 000\, 000| | Giga | |\text{G}| |
| |10^6| | |1\, 000\, 000| | Méga | |\text{M}| |
| |10^3| | |1\, 000| | Kilo | |\text{k}| |
| |10^2| | |100| | Hecto | |\text{h}| |
| |10^1| | |10| | Déca | |\text{da}| |
| |10^{-1}| | |0{,}1| | Déci | |\text{d}| |
| |10^{-2}| | |0{,}01| | Centi | |\text{c}| |
| |10^{-3}| | |0{,}001| | Milli | |\text{m}| |
| |10^{-6}| | |0{,}000\,001| | Micro | |\mu| |
| |10^{-9}| | |0{,}000\,000\,001| | Nano | |\text{n}| |
| |10^{-12}| | |0{,}000\,000\,000\,001| | Pico | |\text{p}| |
Voici quelques exemples d'utilisation de ces préfixes.
|
Julien vient tout juste de se procurer un disque dur externe d'une capacité de |\boldsymbol{5}| gigaoctets. En utilisant les préfixes du système international, on peut connaitre combien d'octets cela représente.||5\:\text{Go}=5\times 10^9\:\text{o}|| |
 source |
|
 |
Chaque gouttelette dans un brouillard a un diamètre d'environ |\boldsymbol{2}| micromètres. Une fois convertie en mètres, cette grandeur correspond à ceci.||2\:\mu\text{m}=2\times 10^{-6}\:\text{m}|| |

