Scientific notation allows very large or very small numbers to be easily expressed and compared. As its name suggests, this notation is used in science to represent measurements. This is why scientific notation is generally only applied to positive numbers.
Scientific notation is composed of 2 factors.
-
The 1st factor, also called the mantissa, is a decimal number |(\boldsymbol{\color{#333FB1}{a}})| that is greater than or equal to |1,| but less than |10,| comprised of the original number’s significant figures.
-
The 2nd factor is a power of |10| expressed in exponential notation. This part indicates the magnitude of the number.
-
The exponent |\boldsymbol{\color{#3A9A38}{n}}| is an integer not equal to zero.
-
If |\boldsymbol{\color{#3A9A38}{n}}\geq1,| the initial number is greater than |1.|
-
If |\boldsymbol{\color{#3A9A38}{n}}\leq-1,| the initial number ranges between |0| and |1.|||\begin{align}\large&\boldsymbol{\color{#333fb1}{a}}\times \boldsymbol{\color{#3a9a38}{10^n}}\\[-3pt] &\!\!\!\!\!\!\boldsymbol{\color{#333fb1}{\nearrow}}\qquad\;\boldsymbol{\color{#3a9a38}{\nwarrow}}\\ \boldsymbol{\color{#333fb1}{1\textbf{st factor}}}&\qquad\ \ \boldsymbol{\color{#3a9a38}{2\textbf{nd factor}}}\\ 1\leq \boldsymbol{\color{#333fb1}{a}}<10&\qquad\ \ \ \ \ \boldsymbol{\color{#3a9a38}{n}}\in\mathbb{Z}^*\end{align}||
-
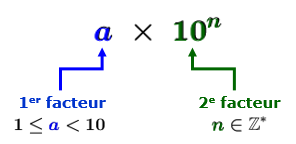
The distance between the Moon and Earth is |384\ 400\:\text{km}.| We can express this number in scientific notation like so:||\boldsymbol{\color{#333fb1}{3.844}}\,\times\,\boldsymbol{\color{#3a9a38}{10^5}}\ \text{km}||
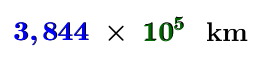
The mosquito has a mass of about |0.00000107\:\text{kg}.| We can express this number in scientific notation like so:||\boldsymbol{\color{#333fb1}{1.07}}\,\times\,\boldsymbol{\color{#3a9a38}{10^{-6}}}\ \text{kg}||The 1st factor is a decimal number that is greater than |1| and less than |10.| It is comprised of the original number’s significant figures.
The 2nd factor indicates the magnitude of the initial number. Since |10^{-6}=0.000001,| this factor indicates that the initial number is in the millionths. In other words, we have:||1.07\times 10^{-6}=1.07\times 0.000001=0.00000107||
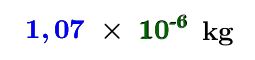
On remarque que le 1er facteur est un nombre décimal supérieur à |1| et inférieur à |10|. Il contient les chiffres significatifs du nombre initial.
Pour ce qui est du 2e facteur, il indique l'ordre de grandeur du nombre initial. Comme |10^{-6}=0{,}000\, 001,| ce facteur indique que le nombre initial est de l'ordre des millionièmes. En d'autres mots, on a ceci.||1{,}07\times 10^{-6}=1{,}07\times 0{,}000\, 001=0{,}000\, 001\, 07||
There are two possible cases to encounter. The number will either be expressed in decimal notation or it will already be expressed as a product of 2 factors, the second of which is a power of |10.| This section presents a method for each of these cases.
-
If the initial number does not have a decimal point, add one to the right of the ones position.
-
Move the decimal point left or right until the number is greater than or equal to |1,| but less than |10.| Count how many places it moved.
-
Write the number in scientific notation.
|\small \bullet| The 1st factor is the number obtained in Step 2 (remove the unnecessary |0|s).
|\small \bullet| The 2nd factor is the number of places the decimal point moved in Step 2.
|\small \circ| If the decimal was moved to the left, the exponent is positive.
|\small \circ| If the decimal was moved to the right, the exponent is negative.
Express the number |85\:200| in scientific notation.
-
If the initial number does not have a decimal point, add one to the right of the ones position.
The initial number is an integer, so it does not have a decimal point. Add a decimal point to the right of the ones position, like so:||85\,200\boldsymbol{\color{#EC0000}{.}}|| -
Move the decimal point to the left or right until the number is greater than or equal to |1,| but less than |10.| Count how many places it moved!
In this example, the decimal point must be moved to the left.||\underset{\ \ \ \ 4\ \text{places}}{8\color{#ec0000}{\boldsymbol{.}\underleftarrow{\color{black}{\!5\ 200}}\boldsymbol{.}}}||Moving the decimal place |\boldsymbol{\color{#7CCA51}{4}}| times to the left gives the number |8.5200.| -
Write the number in scientific notation.
The 1st factor is |\boldsymbol{\color{#333FB1}{8.52}}.| This is found by taking away the unnecessary zeros from the number found in Step 2. Notice that this number ranges between |1| (inclusively) and |10| (exclusively).
The 2nd factor is |\boldsymbol{\color{#3a9a38}{10^4}}.| The exponent corresponds to the number of places moved in Step 2. Since the decimal point moved to the left, the exponent is positive.
The scientific notation for the number |85\ 200| is:||\boldsymbol{\color{#333fb1}{8.52}}\,\times\,\boldsymbol{\color{#3a9a38}{10^{4}}}||

2. Déplacer la virgule par bonds vers la gauche ou vers la droite, jusqu'à l'obtention d'un nombre plus grand ou égal à |1,| mais plus petit que |10.| Compter le nombre de bonds!
Il faut déplacer la virgule vers la gauche.
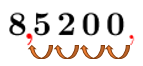
Après 4 bonds vers la gauche, on obtient le nombre |8{,}5200.|
3. Écrire le nombre en notation scientifique.
Le 1er facteur correspond à |\color{blue}{8{,}52}|. On l'obtient en enlevant les zéros inutile au nombre obtenu à l'étape 2. On remarque que ce nombre est compris entre |1| inclusivement et |10| exclusivement.
Le 2e facteur correspond à |\color{green}{10^4}|. L'exposant correspond au nombre de bonds effectués à l'étape 2. Comme on a effectué les bonds vers la gauche, l'exposant est positif.
On obtient donc que la notation scientifique du nombre |85\ 200| est :
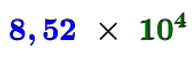
Express the number |0.00002056| in scientific notation.
-
If the initial number does not have a decimal point, add it to the right of the ones position.
This number already contains a decimal point, so we can go directly to Step 2.||0\boldsymbol{\color{#EC0000}{.}}00002056|| -
Move the decimal point left or right until the number is greater than or equal to |1,| but less than |10.| Count how many places it moved!
In this example, the decimal point must be moved to the right.||\underset{\!\!\!\!\!\!5\ \text{places}}{0\color{#ec0000}{\boldsymbol{.}\underrightarrow{\color{black}{\!00002}}\boldsymbol{.}\color{black}{056}}}||After moving |\boldsymbol{\color{#3A9A38}{5}}| places to the right, we get the number |2.056.| -
Write the number in scientific notation.
The 1st factor is |\boldsymbol{\color{#333FB1}{2.056}}.| Notice that this number ranges between |1| (inclusively) and |10| (exclusively).
The 2nd factor is |\boldsymbol{\color{#3A9A38}{10^{\text{-}5}}}.| The exponent corresponds to the number of places moved in Step 2. Since the decimal was moved to the right, the exponent is negative.
So, the number |0.00002056| in scientific notation is:||\boldsymbol{\color{#333fb1}{2.056}}\,\times\,\boldsymbol{\color{#3a9a38}{10^{-5}}}||

2. Déplacer la virgule par bonds vers la gauche ou vers la droite, jusqu'à l'obtention d'un nombre plus grand ou égal à |1,| mais plus petit que |10.| Compter le nombre de bonds!
Il faut déplacer la virgule vers la droite.
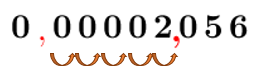
Après 5 bonds vers la droite, on obtient le nombre |2{,}056.|
3.Écrire le nombre en notation scientifique
Le 1erfacteur correspond à |\color{blue}{2{,}056}|. On remarque que ce nombre est compris entre |1| inclusivement et |10| exclusivement.
Le 2e facteur correspond à |\color{green}{10^{\text{-}5}}|. L'exposant correspond au nombre de bonds effectués à l'étape 2. Comme on a fait les bonds vers la droite, l'exposant est négatif.
On obtient donc que la notation scientifique du nombre |0{,}000\,020\,56| est :

Here are some other examples.
||\begin{align}356\: 200&=3.562\times 10^5 & &\quad & 0.0013&=1.3\times 10^{-3}\\ \\ 404\,000\,000&=4.04\times 10^8 & &\quad & 0.000007&=7\times 10^{-6}\end{align}||
In some situations, the number to be expressed in scientific notation may already be written as a product of factors, such as these:||0.03\ \times\ 10^{5}\qquad \qquad 432.4\ \times\ 10^{-10}||
It may seem like these numbers are already expressed in scientific notation, but be careful! The 1st factor does not range between |1| (inclusively) and |10| (exclusively). This means they are not written in scientific notation.
Here's the method to convert these numbers to scientific notation:
-
Convert the 1st factor so that it is a number between |1| (inclusively) and |10| (exclusively) by multiplying or dividing it by the appropriate power of |10.|
-
To conserve the value of the number, perform the inverse operation on the 2nd factor:
If the 1st factor was multiplied by a power of |10,| the 2nd factor must be divided by that same power.
If the 1st factor was divided by a power of |10,| the 2nd factor must be multiplied by that same power.
Express the number |356.2\ \times\ 10^7| in scientific notation.
-
Convert the 1st factor so that it is a number between | \boldsymbol{1}| (inclusively) and | \boldsymbol{10}| (exclusively) by multiplying or dividing it by the appropriate power of | \boldsymbol{10.}|
The 1st factor of the number is |356.2.| To convert it to a number between |1| (inclusively) and |10| (exclusively), divide it by |100,| or by |10^2.| This gives:||356.2\div 10^2=\boldsymbol{\color{#333FB1}{3.562}}|| -
Perform the inverse operation on the 2nd factor.
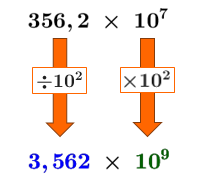
To conserve the value of the number, multiply the 2nd factor by |10^2.| Using the properties of exponents, |10^7\times 10^2=10^{7+2}=\boldsymbol{\color{#3A9A38}{10^9}}| is obtained.||\large 356.2\,\times\,10^7\\ \downarrow\qquad\ \ \ \ \downarrow\\ \boxed{\div10^2}\quad\ \ \boxed{\times 10^2}\\ \downarrow\qquad\ \ \ \ \downarrow\\ \large \boldsymbol{\color{#333fb1}{3.562}}\,\times\,\boldsymbol{\color{#3a9a38}{10^9}}||
Express the number |0.121\ \times 10^{-14}| in scientific notation.
-
Convert the 1st factor so that it is a number between | \boldsymbol{1}| (inclusively) and | \boldsymbol{10}| (exclusively) by multiplying or dividing it by the appropriate power of | \boldsymbol{10.}|
The 1st factor is |\small 0.121.| To convert it into a number between |1| (inclusively) and |10| (exclusively), multiply it by |10| or by |10^1.| This gives:||0.121\times 10=\color{#333FB1}{1.21}|| -
Perform the inverse operation on the 2nd factor.
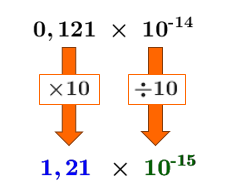
To conserve the value of the number, divide the 2nd factor by |10.| Using the properties of exponents, gives |10^{-14}\div 10=10^{-14-1}=\color{#3A9A38}{10^{-15}}.|||\large 0.121\,\times\,10^{-14}\\ \downarrow\qquad\ \ \ \ \downarrow\\ \boxed{\times 10}\quad\ \ \boxed{\div 10}\\ \downarrow\qquad\ \ \ \ \downarrow\\ \large \boldsymbol{\color{#333fb1}{1.21}}\,\times\,\boldsymbol{\color{#3a9a38}{10^{-15}}}||
To add or subtract numbers in scientific notation, they must first be set to the same order of magnitude. In other words, they must be expressed using the same power of |10.| Here is how to do this:
-
Identify the number in scientific notation with the greatest power of |10.|
-
Express the other number using this power of |10.|
-
Add or subtract the numbers by adding or subtracting only the 1st factors.
-
Express the answer in scientific notation, as needed.
Perform the following operation and express the answer in scientific notation.||5.6\times 10^5+4.42\times 10^7||
-
Identify the number in scientific notation with the greatest power of |\boldsymbol{10.}|
The number with the greatest power of |10| is |4.42\times 10^7.| -
Express the other number using this power of |10.|
To express the number |5.6\times 10^5| in the power of |10^7,| multiply the 2nd factor of the number by |10^2.| To conserve the value of the number, divide the 1st factor by |10^2.|||\large 5.6\,\times\,10^{5}\\ \downarrow\qquad\ \ \ \ \downarrow\\ \boxed{\div 10^2}\quad\ \ \boxed{\times 10^2}\\ \downarrow\qquad\ \ \ \ \downarrow\\ \large 0.056\,\times\,10^{7}|| -
Add the numbers by adding only the 1st factors.
The following is obtained:||\boldsymbol{\color{#333fb1}{0.056}}\times 10^7+\boldsymbol{\color{#333fb1}{4.42}}\times 10^7=\boldsymbol{\color{#333fb1}{4.476}}\times 10^7|| -
Express the answer in scientific notation, as needed.
Since the sum of the 1st factors ranges between |1| (inclusively) and |10| (exclusively), it is already in scientific notation. No further changes are needed. The answer is:||\boldsymbol{\color{#333fb1}{4.476}}\times \boldsymbol{\color{#3a9a38}{10^7}}||

3. Additionner les nombres en additionnant les 1er facteurs seulement.
On peut maintenant effectuer l'opération.
||\color{blue}{0,056}\times 10^7+\color{blue}{4,42}\times 10^7=\color{blue}{4,476}\times 10^7||
4. Exprimer le résultat en notation scientifique, au besoin.
Comme le 1er facteur du résultat est compris entre |\small 1| inclusivement et |\small 10| exclusivement, il est déjà en notation scientifique. Il n'y a pas de changement à faire. La réponse est donc: ||\color{blue}{4,476}\times \color{green}{10^7}||
Perform the following operation and express the answer in scientific notation.||1.3\times 10^{-4}-7.9\times 10^{-5}||
-
Identify the number in scientific notation with the greatest power of |\boldsymbol{10.}|
The number with the greatest power of |10| is |1.3\times 10^{-4}.| -
Express the other number using this power of |\boldsymbol{10.}|
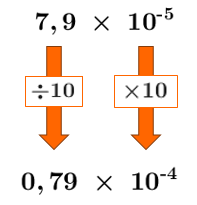
To express the number |7.9\times 10^{-5}| using the power of |10^{-4},| multiply the 2nd factor of the number by |10^1.| To conserve the value of the number, we also divide the 1st factor by |10^1.|||\large 7.9\,\times\,10^{-5}\\ \downarrow\qquad\ \ \ \ \downarrow\\ \boxed{\div 10}\quad\ \ \boxed{\times 10}\\ \downarrow\qquad\ \ \ \ \downarrow\\ \large 0.79\,\times\,10^{-4}|| -
Subtract numbers by subtracting only the 1st factors.
The following is obtained:||\boldsymbol{\color{#333fb1}{1.3}}\times 10^{-4}-\boldsymbol{\color{#333fb1}{0.79}}\times 10^{-4}=\boldsymbol{\color{#333fb1}{0.51}}\times 10^{-4}|| -
Express the answer in scientific notation, as needed.
The 1st factor does not range between |1| (inclusively) and |10| (exclusively). The following changes must be made to put the answer in scientific notation.||\large 0.51\,\times\,10^{-4}\\ \downarrow\qquad\ \ \ \ \downarrow\\ \boxed{\times 10}\quad\ \ \boxed{\div 10}\\ \downarrow\qquad\ \ \ \ \downarrow\\ \large \boldsymbol{\color{#333fb1}{5.1}}\,\times\,\boldsymbol{\color{#3a9a38}{10^{-5}}}||
3. Soustraire les nombres en soustrayant les 1er facteurs seulement.
On peut maintenant effectuer l'opération.
||\color{blue}{1,3}\times 10^{\text{-}4}-\color{blue}{0,79}\times 10^{\text{-}4}=\color{blue}{0,51}\times 10^{\text{-}4}||
4. Exprimer le résultat en notation scientifique, au besoin.
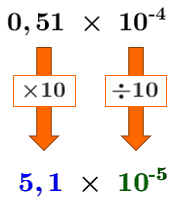
Le 1er facteur n'est pas inclus entre |\small 1| inclusivement et |\small 10| exclusivement. On doit donc effectuer les changements suivants pour obtenir une réponse en notation scientifique.
There are a few methods to multiply or divide numbers in scientific notation. Here is one:
-
Multiply or divide the 1st factors together and then the 2nd factors together.
-
Express the answer in scientific notation, as needed.
Perform the following operation and express the answer in scientific notation.||2.9\times 10^{15}\quad \times \quad 8.1\times 10^{-3}||
-
Multiply the 1st factors together and then the 2nd factors together.||\begin{align}&\boldsymbol{\color{#333fb1}{2.9}}\times \boldsymbol{\color{#3a9a38}{10^{15}}} \times\, \boldsymbol{\color{#333fb1}{8.1}}\times \boldsymbol{\color{#3a9a38}{10^{-3}}}\\[5pt]=\, (&\boldsymbol{\color{#333fb1}{2.9}}\times\boldsymbol{\color{#333fb1}{8.1}})\ \times (\boldsymbol{\color{#3a9a38}{10^{15}}}\times \boldsymbol{\color{#3a9a38}{10^{-3}}})\\[5pt] =\ &\boldsymbol{\color{#333fb1}{23.49}} \times \boldsymbol{\color{#3a9a38}{10^{15-3}}}\\[5pt] =\ &\boldsymbol{\color{#333fb1}{23.49}}\times \boldsymbol{\color{#3a9a38}{10^{12}}} \end{align}||
-
Express the answer in scientific notation, as needed.
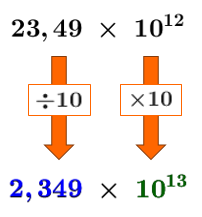
Since the first factor calculated does not range between |1| (inclusively) and |10| (exclusively), the following changes must be made to put the answer in scientific notation.||\large 23.49\,\times\,10^{12}\\ \downarrow\qquad\ \ \ \ \downarrow\\ \boxed{\div 10}\quad\ \ \boxed{\times 10}\\ \downarrow\qquad\ \ \ \ \downarrow\\ \large \boldsymbol{\color{#333fb1}{2.349}}\,\times\,\boldsymbol{\color{#3a9a38}{10^{13}}}||
Perform the following operation and express the answer in scientific notation.||\dfrac{7.8\times 10^{-2}}{1.5\times 10^{-8}}||
-
Divide the 1st factors together and then the 2nd factors together.||\begin{align}\dfrac{\boldsymbol{\color{#333fb1}{7.8}}\times \boldsymbol{\color{#3a9a38}{10^{-2}}}}{\boldsymbol{\color{#333fb1}{1.5}}\times \boldsymbol{\color{#3a9a38}{10^{-8}}}}&=\dfrac{\boldsymbol{\color{#333fb1}{7.8}}}{\boldsymbol{\color{#333fb1}{1.5}}} \times \dfrac{\boldsymbol{\color{#3a9a38}{10^{-2}}}}{\boldsymbol{\color{#3a9a38}{10^{-8}}}}\\[5pt] &=\,\boldsymbol{\color{#333fb1}{5.2}}\ \times\ \boldsymbol{\color{#3a9a38}{10^{-2-^-8}}}\\[5pt] &=\,\boldsymbol{\color{#333fb1}{5.2}}\ \times\ \boldsymbol{\color{#3a9a38}{10^6}}\end{align}||
-
Express the answer in scientific notation, as needed.
Since the 1st factor calculated ranges between |1| (inclusively) and |10| (exclusively), it is already in scientific notation. No further changes are needed. The answer is:||\boldsymbol{\color{#333fb1}{5.2}}\ \times\ \boldsymbol{\color{#3a9a38}{10^6}}||
To simplify writing very large or very small numbers, the international system provides prefixes related to scientific notation. Here are some examples:
| Power of 10 | Number | Prefix | Symbol |
|---|---|---|---|
| |10^{12}| | | 1\ 000\ 000\ 000\ 000| | Tera | |\text{T}| |
| |10^9| | | 1\ 000\ 000\ 000| | Giga | |\text{G}| |
| |10^6| | | 1\ 000\ 000| | Mega | |\text{M}| |
| |10^3| | | 1000| | Kilo | |\text{k}| |
| |10^2| | |100| | Hecto | |\text{h}| |
| |10^1| | |10| | Deca | |\text{da}| |
| |10^{-1}| | |0.1| | Deci | |\text{d}| |
| |10^{-2}| | |0.01| | Centi | |\text{c}| |
| |10^{-3}| | |0.001| | Milli | |\text{m}| |
| |10^{-6}| | | 0.000001| | Micro | |\mu| |
| |10^{-9}| | | 0.000000001| | Nano | |\text{n}| |
| |10^{-12}| | | 0.000000000001| | Pico | |\text{p}| |
Here are some examples of how these prefixes are used.
|
Julian just bought an external hard drive with a capacity of |\boldsymbol{5}| gigabytes. Using the prefixes from the international system, we can determine how many bytes it can store.||5\:\text{GB}=5\times 10^9\:\text{B}|| |
 source |
|
 |
Each water droplet in a fog cloud has a diameter of about |\boldsymbol{2}| micrometres. When converted to metres, this size is equivalent to:||2\:\mu\text{m}=2\times 10^{-6}\:\text{m}|| |

