En plus de comparer la norme des différents vecteurs, on peut également analyser leur position. Plus précisément, on va s'attarder à la projection orthogonale des vecteurs.
Soit deux vecteurs |\overrightarrow{u}| et |\overrightarrow{v}.| On appelle la projection orthogonale de |\overrightarrow{u}| sur |\overrightarrow{\large v}| le vecteur |\overrightarrow{u}_{\overrightarrow{\large v}}.| L'origine du vecteur projection est la même que celle des vecteurs |\overrightarrow{u}| et |\overrightarrow{v}.| L'extrémité du vecteur projection coïncide avec la perpendiculaire issue de l'extrémité de |\overrightarrow {u}.|
On utilise aussi l'appellation « vecteur projeté ».

-
Le mot « orthogonale » indique que la projection se fait à 90°.
-
|\overrightarrow{u}_{\overrightarrow{\Large v}}| est parallèle à |\overrightarrow{v}.|
-
La projection orthogonale d'un vecteur nul n'est pas possible.
Il y a trois cas possibles lors de la projection orthogonale d'un vecteur :
| Angle aigu |  |
| Angle obtus |  |
| Angle droit | 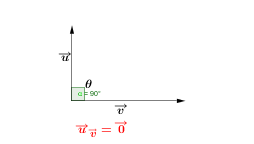 |
Il existe une formule afin de calculer les composantes de la projection orthogonale d'un vecteur.
Soit |\overrightarrow{u}| et |\overrightarrow{v}|, alors
||\overrightarrow{u}_{\overrightarrow{\Large v}} = \dfrac{\overrightarrow{u} \cdot \overrightarrow{v}}{\mid \mid \overrightarrow{v} \mid \mid ^2} \overrightarrow{v}||
Malgré l'allure plutôt complexe de la fraction |\dfrac{\overrightarrow{u} \cdot \overrightarrow{v}}{\mid \mid \overrightarrow{v} \mid \mid ^2},| il s'agit d'un simple scalaire. La démonstration de cette formule sera faite après l'exemple qui suit.
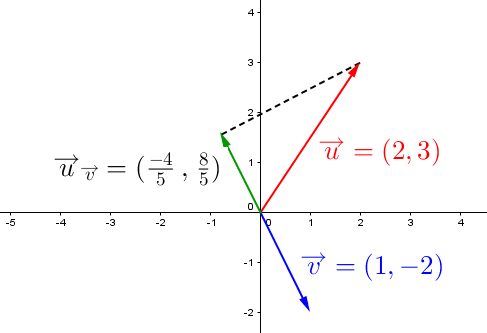
Soit les vecteurs |\overrightarrow{u}=(2,3)| et |\overrightarrow{v}=(1,-2)|. Déterminez les composantes de |\overrightarrow{u}_{\overrightarrow{\Large v}}|.
1) Effectuer le produit scalaire
||\begin{align} \overrightarrow{u} \cdot \overrightarrow{v} &= (2,3) \cdot (1,-2) \\
&= 2 \times 1 + 3 \times -2 \\
&= -4\end{align}||
2) Calculer la norme
||\begin{align} \mid \mid \overrightarrow{v} \mid \mid ^2 &= \left(\sqrt{1^2+(-2)^2}\right)^2\\
&=5\end{align}||
3) Appliquer la formule
||\begin{align} \overrightarrow{u}_{\overrightarrow{\Large v}}&=\frac{\overrightarrow{u} \cdot \overrightarrow{v}}{\mid \mid \overrightarrow{v} \mid \mid ^2}\ \overrightarrow{v} \\
&= \frac{-4}{5}\ \overrightarrow{v}\\
&= \frac{-4}{5}\ \big(1,-2\big)\\
&= \left( \frac{-4}{5},\frac{8}{5} \right)\end{align}||
Une fois de plus, on peut utiliser le plan cartésien pour représenter le tout.
Pour effectuer la démonstration de la formule permettant de trouver les composantes de la projection orthogonale d'un vecteur nous allons avoir besoin du schéma suivant :

1. On peut affirmer que
||\overrightarrow{u}_{\overrightarrow{\Large v}} \parallel \overrightarrow{v}||
2. Comme les deux vecteurs précédents sont parallèles, il existe un scalaire |k| tel que
||\overrightarrow{u}_{\overrightarrow{\Large v}} = k \overrightarrow{v}||
3. Comme nous utilisons une projection orthogonale (à 90°), on peut affirmer que
||(\overrightarrow{u}-\overrightarrow{u}_\overrightarrow{\Large v}) \perp \overrightarrow{v}||
4. En utilisant le résultat obtenu à l'étape 2. on peut substituer |\overrightarrow{u}_{\overrightarrow{\Large v}}| par |k\overrightarrow{v}|.
On obtient alors
||(\overrightarrow{u}-k\overrightarrow{v}) \perp \overrightarrow{v}||
5. Deux vecteurs perpendiculaires (orthogonaux) ont forcément un produit scalaire nul.
||(\overrightarrow{u}-k\overrightarrow{v})\cdot \overrightarrow{v}=0||
6. En appliquant la distributivité du produit scalaire:
||\overrightarrow{u} \cdot \overrightarrow{v} - k\overrightarrow{v} \cdot \overrightarrow{v}=0||
7. On isole |k| dans l'égalité précédente.
||k = \displaystyle \frac{\overrightarrow{u} \cdot \overrightarrow{v}}{\overrightarrow{v} \cdot \overrightarrow{v}}||
8. On utilise le fait que
||\overrightarrow{v} \cdot \overrightarrow{v} = \mid \mid \overrightarrow{v} \mid \mid ^2||
Donc,
||k= \displaystyle \frac{\overrightarrow{u} \cdot \overrightarrow{v}}{\mid \mid \overrightarrow{v} \mid \mid ^2}||
9. En substitutiant |k| dans l'étape 2. on obtient le résultat voulu,
||\overrightarrow{u}_{\overrightarrow{\Large v}} = \frac{\overrightarrow{u} \cdot \overrightarrow{v}}{\mid \mid \overrightarrow{v} \mid \mid ^2} \overrightarrow{v}||
Il arrive fréquemment que l'on veuille seulement connaitre la norme du vecteur projeté et non ses composantes.
||{\parallel}\overrightarrow{u}_{ \overrightarrow{\Large v}}{\parallel} = {\parallel}\overrightarrow{u}{\parallel} \cos \theta||où
|\overrightarrow{u}_{\overrightarrow{\Large v}}| est le vecteur projeté
|\overrightarrow{v}| est le vecteur sur lequel on projette |\overrightarrow{u}|
|\theta| est l'angle aigu entre |\overrightarrow {u}| et |\overrightarrow{v}|

Soit |{\parallel}\overrightarrow{u}{\parallel} = 5,| |{\parallel}\overrightarrow{v}{\parallel} = 3| et |\theta = 35^\circ|. Détermine |{\parallel}\overrightarrow{u}_{\overrightarrow{\Large v}}{\parallel}.|
1) Calculer la norme de |\overrightarrow {u}|
Dans cette situation, la norme de ce vecteur est déjà donné.
||{\parallel}\overrightarrow{u}{\parallel} = 5||
2) Calculer la mesure de |\theta|
Une fois de plus, cette mesure est fournie dans l'énoncé.
||\theta = 35^\circ||
3) Appliquer la formule
||\begin{align} {\parallel}\overrightarrow{u}_{ \overrightarrow{\Large v}}{\parallel} &= {\parallel}\overrightarrow{u}{\parallel} \cos \theta\\
&= 5 \cos 35^\circ \\
&\approx 4{,}1 \end{align}||
4) Interpréter la réponse
La norme de |\overrightarrow {u}_\overrightarrow{v}| est d'environ |4{,}1| unités.
Remarque : La norme du vecteur |\overrightarrow{v}| n'était pas une information utile.
Pour valider ta compréhension à propos des vecteurs de façon interactive, consulte la MiniRécup suivante :
