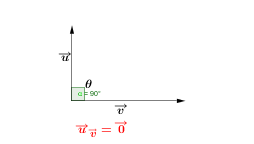In addition to comparing the magnitudes (norms) of different vectors, it is possible to consider their positions relative to each other. We will focus on the orthogonal projection of vectors.
Given two vectors, |\overrightarrow{u}| and |\overrightarrow{v},| the vector |\overrightarrow{u}_{\overrightarrow{\large v}}| is the orthogonal projection of |\overrightarrow{u}| on |\overrightarrow{\large v}.| The origin of the vector projection is the same as that of the vectors |\overrightarrow{u}| and |\overrightarrow{v}.| The tip of the vector projection coincides with the perpendicular line drawn from the tip of |\overrightarrow {u}| to |\overrightarrow{v}.|
The terms orthogonal projection and vector projection are interchangeable.

-
The word orthogonal indicates that the projection is made at a 90° angle.
-
|\overrightarrow{u}_{\overrightarrow{\Large v}}| is parallel to |\overrightarrow{v}.|
-
Orthogonally projecting the zero vector is not possible.
There are three possible situations when orthogonally projecting a vector.
|
Acute angle |
|
|
Obtuse angle |
|
|
Right angle |
|
There is a formula for calculating the components of a vector projection.
Given |\overrightarrow{u}| and |\overrightarrow{v}|, we have:
||\overrightarrow{u}_{\overrightarrow{\Large v}} = \dfrac{\overrightarrow{u} \cdot \overrightarrow{v}}{\mid \mid \overrightarrow{v} \mid \mid ^2} \overrightarrow{v}||
Despite the rather complex appearance of the fraction |\dfrac{\overrightarrow{u} \cdot \overrightarrow{v}}{\mid \mid \overrightarrow{v} \mid \mid ^2},| it is ultimately a simple scalar. The proof of this formula will be shown after the following example.
Let the vectors be |\overrightarrow{u}=(2,3)| and |\overrightarrow{v}=(1,-2)|. Determine the components of |\overrightarrow{u}_{\overrightarrow{\Large v}}|.
-
Calculate the dot product ||\begin{align} \overrightarrow{u} \cdot \overrightarrow{v} &= (2,3) \cdot (1,-2) \\
&= 2 \times 1 + 3 \times -2 \\
&= -4\end{align}|| -
Calculate the magnitude (norm) ||\begin{align} \mid \mid \overrightarrow{v} \mid \mid ^2 &= \left(\sqrt{1^2+(-2)^2}\right)^2\\
&=5\end{align}|| -
Apply the formula ||\begin{align} \overrightarrow{u}_{\overrightarrow{\Large v}}&=\frac{\overrightarrow{u} \cdot \overrightarrow{v}}{\mid \mid \overrightarrow{v} \mid \mid ^2}\ \overrightarrow{v} \\
&= \frac{-4}{5}\ \overrightarrow{v}\\
&= \frac{-4}{5}\ \big(1,-2\big)\\
&= \left( \frac{-4}{5},\frac{8}{5} \right)\end{align}||
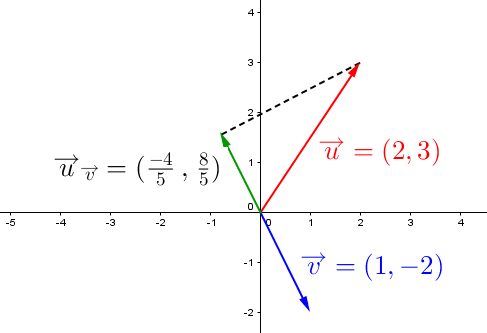
Once again, use the Cartesian plane to represent everything.
To prove the formula for calculating the components of a vector projection, see the following diagram.

-
It is clear that ||\overrightarrow{u}_{\overrightarrow{\Large v}} \parallel \overrightarrow{v}||
-
As the two vectors are parallel, there must be a scalar |k| such that: ||\overrightarrow{u}_{\overrightarrow{\Large v}} = k \overrightarrow{v}||
-
Projecting orthogonally (at 90°), we have that ||(\overrightarrow{u}-\overrightarrow{u}_\overrightarrow{\Large v}) \perp \overrightarrow{v}||
-
Using the equation obtained in step 2, substitute |\overrightarrow{u}_{\overrightarrow{\Large v}}| par |k\overrightarrow{v}.|
The result is: ||(\overrightarrow{u}-k\overrightarrow{v}) \perp \overrightarrow{v}|| -
Two perpendicular (orthogonal) vectors have a dot product of zero. ||(\overrightarrow{u}-k\overrightarrow{v})\cdot \overrightarrow{v}=0||
-
Apply the distributive property of the dot product. ||\overrightarrow{u} \cdot \overrightarrow{v} - k\overrightarrow{v} \cdot \overrightarrow{v}=0||
-
Isolate |k|. ||k = \displaystyle \frac{\overrightarrow{u} \cdot \overrightarrow{v}}{\overrightarrow{v} \cdot \overrightarrow{v}}||
-
We use the fact that: ||\overrightarrow{v} \cdot \overrightarrow{v} = \mid \mid \overrightarrow{v} \mid \mid ^2||
Therefore, ||k= \displaystyle \frac{\overrightarrow{u} \cdot \overrightarrow{v}}{\mid \mid \overrightarrow{v} \mid \mid ^2}|| -
By substituting |k| into step 2, we obtain the desired result. ||\overrightarrow{u}_{\overrightarrow{\Large v}} = \frac{\overrightarrow{u} \cdot \overrightarrow{v}}{\mid \mid \overrightarrow{v} \mid \mid ^2} \overrightarrow{v}||
It often happens that you only need to know the magnitude (norm) of the projected vector, not its components.
||{\parallel}\overrightarrow{u}_{ \overrightarrow{\Large v}}{\parallel} = {\parallel}\overrightarrow{u}{\parallel} \cos \theta||where
|\overrightarrow{u}_{\overrightarrow{\Large v}}| is the vector projection
|\overrightarrow{v}| is the vector on which |\overrightarrow{u}| is projected
|\theta| is the acute angle between |\overrightarrow {u}| and |\overrightarrow{v}|

Let |{\parallel}\overrightarrow{u}{\parallel} = 5,| |{\parallel}\overrightarrow{v}{\parallel} = 3| and |\theta = 35^\circ|. Determine |{\parallel}\overrightarrow{u}_{\overrightarrow{\Large v}}{\parallel}.|
-
Calculate the magnitude of |\overrightarrow {u}|
In this problem, the magnitude of the vector is already given. ||{\parallel}\overrightarrow{u}{\parallel} = 5|| -
Calculate |\theta|
Again, this measurement is provided in the problem. ||\theta = 35^\circ|| -
Apply the formula ||\begin{align} {\parallel}\overrightarrow{u}_{ \overrightarrow{\Large v}}{\parallel} &= {\parallel}\overrightarrow{u}{\parallel} \cos \theta\\
&= 5 \cos 35^\circ \\
&\approx 4.1 \end{align}|| -
Interpret the answer
The magnitude of |\overrightarrow {u}_\overrightarrow{v}| is about |4.1| units.
Note: The magnitude of the vector |\overrightarrow{v}| did not contain any necessary information in this problem.
Pour valider ta compréhension à propos des vecteurs de façon interactive, consulte la MiniRécup suivante :