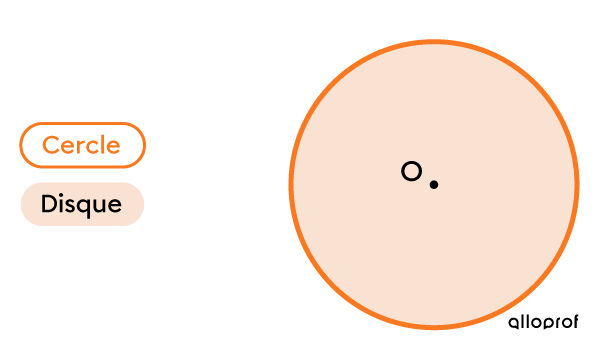
Le cercle est une figure plane formée d’une ligne courbe et fermée. Tous les points de cette ligne courbe sont situés à une distance égale du centre du cercle (O).
Exemple :
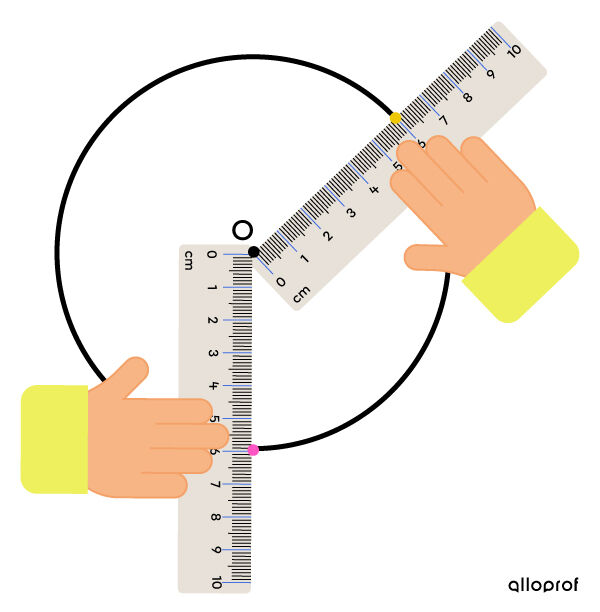
Les points jaune et rose sont à une distance égale du centre du cercle.
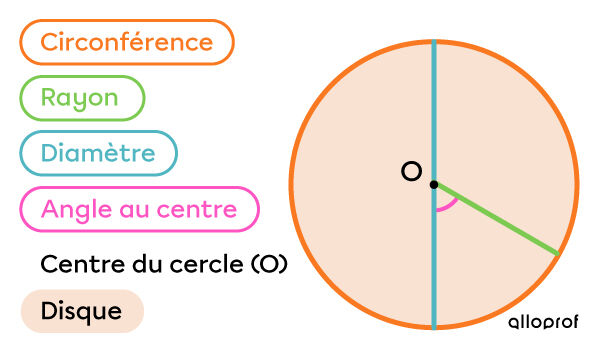
Tu peux décrire les différentes parties d’un cercle à l’aide d’un vocabulaire précis.
Voici un cercle et ses différentes parties :
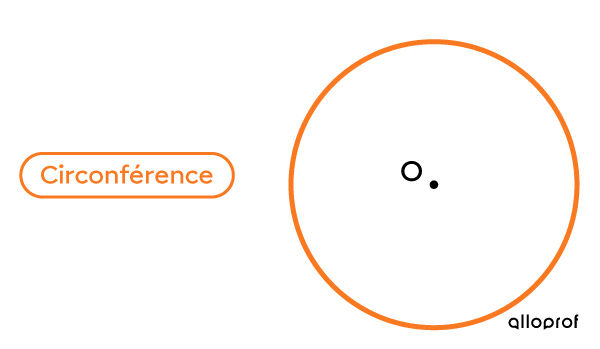
La circonférence est la mesure de la ligne qui forme le contour d’un cercle.
Exemple :
Le rayon d’un cercle est une ligne droite (segment) qui relie le centre du cercle (O) à n’importe quel point du contour du cercle.
Exemple :

Le rayon peut être mesuré à plusieurs endroits du cercle.
Exemple :
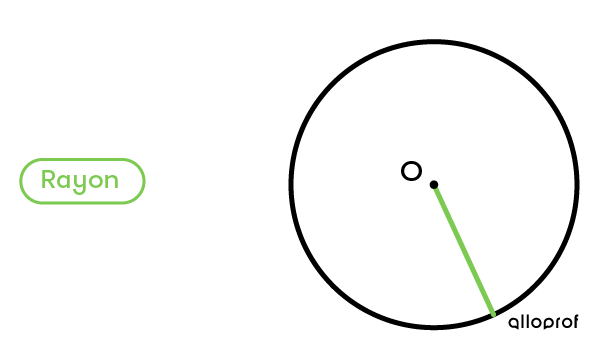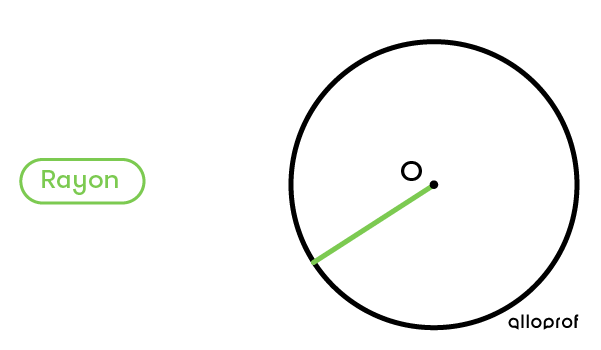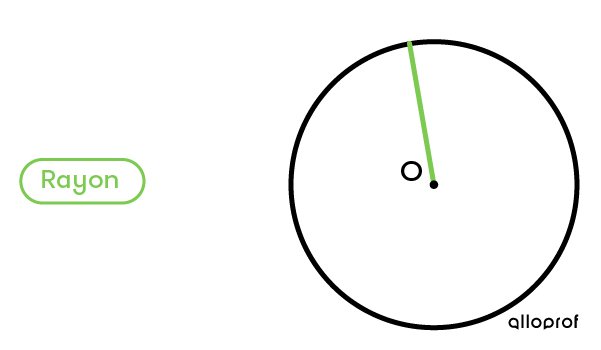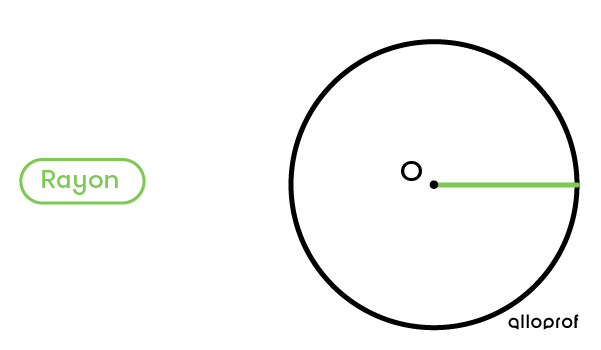
La mesure du rayon correspond toujours à la moitié du diamètre.
Ce cercle a un diamètre de 10 centimètres (cm). Quelle est la mesure de son rayon?
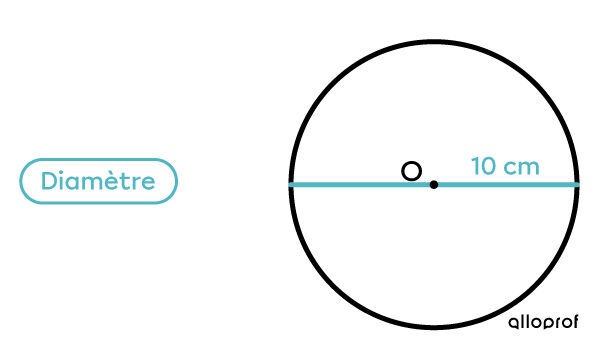
|
Je divise la mesure du diamètre par 2. 10 ÷ 2 = 5 |
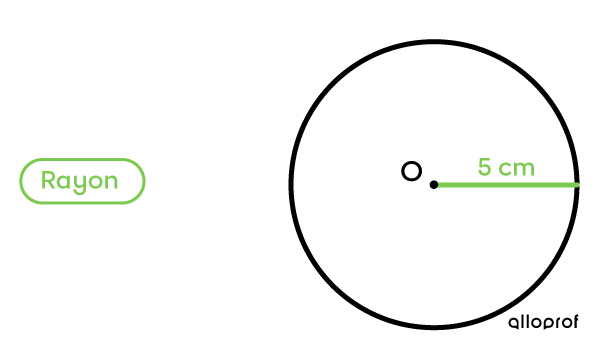 |
Le cercle a un rayon de 5 cm.
Le diamètre d’un cercle est une ligne droite (segment) qui relie deux points du cercle et qui passe obligatoirement par le centre (O).
Exemple :
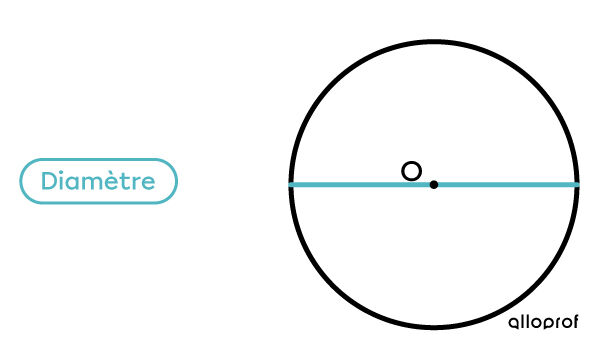
Le diamètre peut être mesuré à plusieurs endroits du cercle.
Exemple :
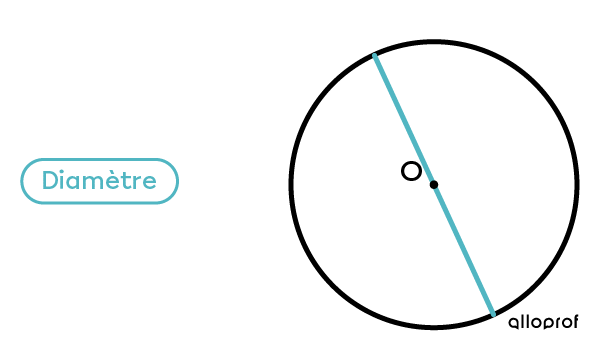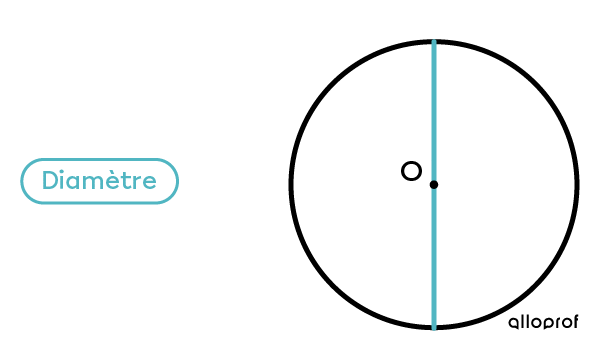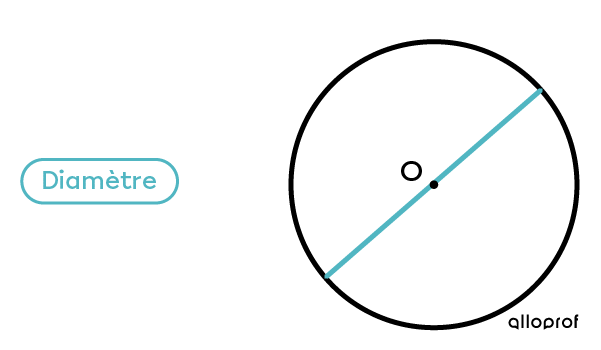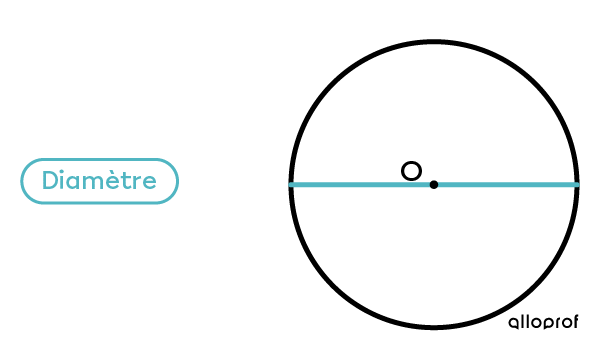
La mesure du diamètre correspond toujours au double du rayon.
Ce cercle a un rayon de 6 centimètres (cm). Quelle est la mesure de son diamètre?
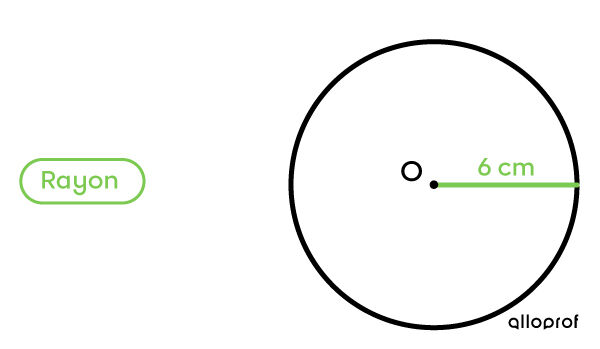
|
Je multiplie la mesure du rayon par 2. 6 × 2 = 12 |
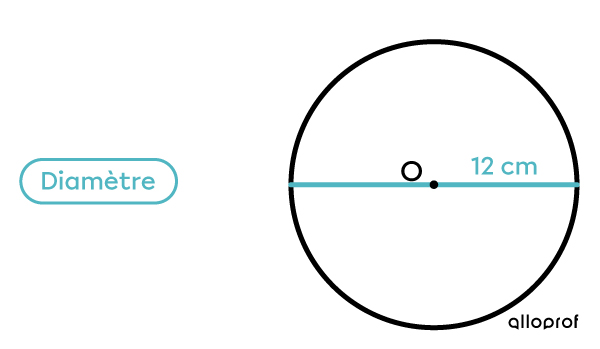 |
Le cercle a un diamètre de 12 cm.
L’angle au centre d’un cercle est un angle (|\angle|) formé par 2 rayons et dont le sommet se situe au centre du cercle (O).
Exemple :

L’angle au centre de cet exemple s’écrit |\angle|AOB.
La mesure de l’angle au centre du cercle se situe entre 0° et 360°.
Pour savoir comment mesurer un angle à l’aide d’un rapporteur d’angles, tu peux lire la fiche Mesurer des angles avec un rapporteur d'angles (à venir).
Le disque est la surface délimitée par le cercle.
Exemple :