A circle is a plane figure formed by a curved and closed line. All points on the curved line are located at an equal distance from the centre of the circle (O).
Example:
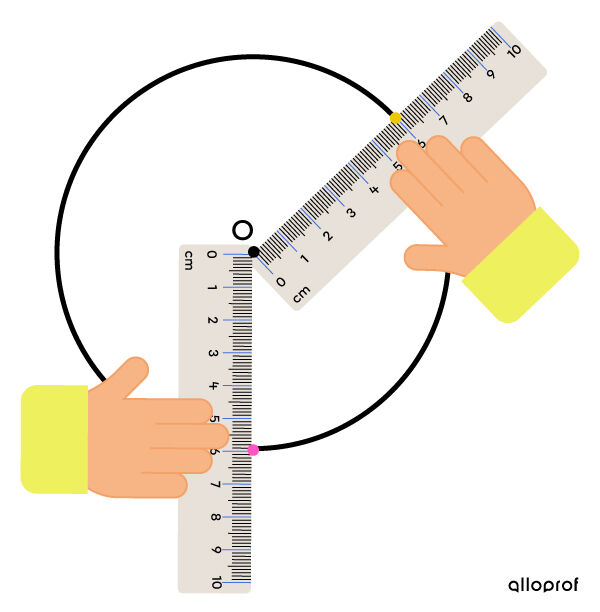
The yellow and pink dots are at an equal distance from the centre of the circle.
The different parts of a circle can be described using specific vocabulary.
Here is a circle and its different parts.

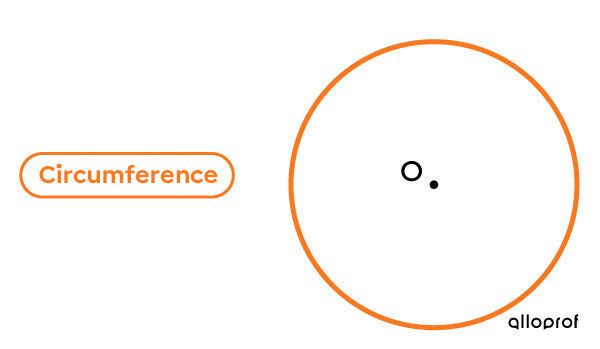
The circumference is the measurement of the line that forms the circle’s contour.
Example:
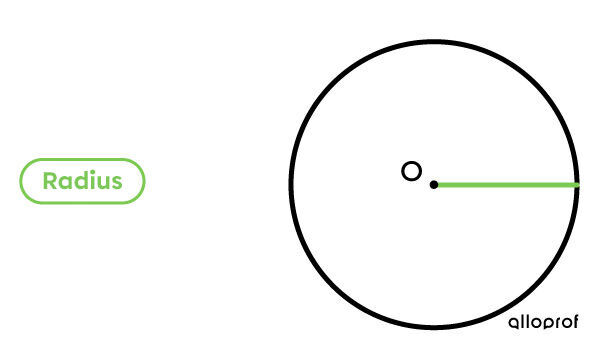
The radius of a circle is a straight line (segment) connecting the centre of the circle (O) to any point on the circle’s contour.
Example:
The radius can be measured at any point on the circle.
Example:
The measurement of the radius is always half the diameter.
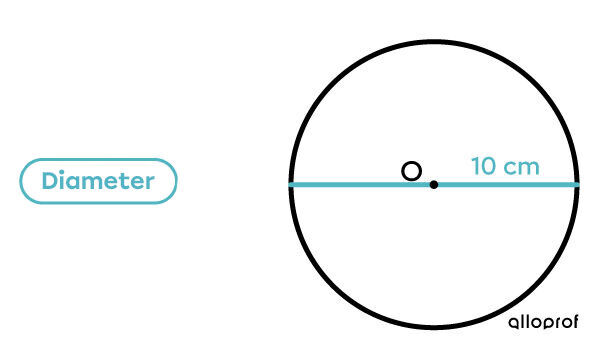
This circle has a diameter of |10| centimetres (cm). What is the measurement of the radius?
|
Divide the measurement of the diameter by |2.| |10\div 2 = 5| |
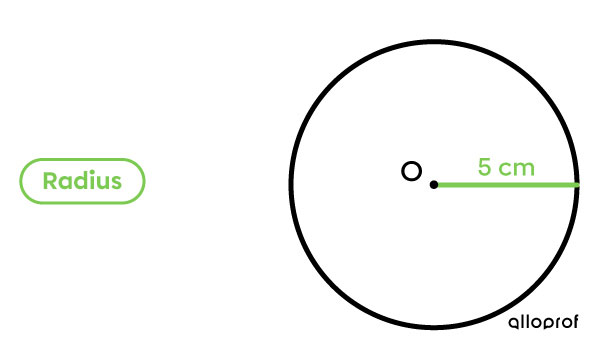 |
The circle has a radius of |5| cm.
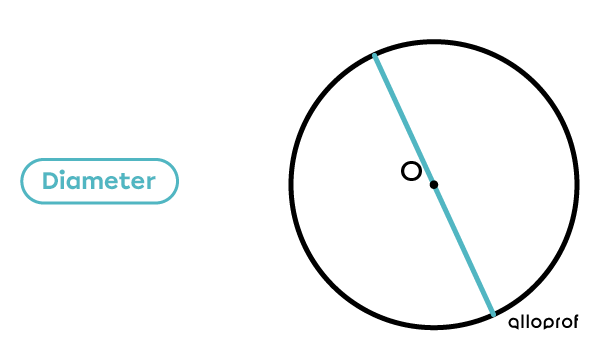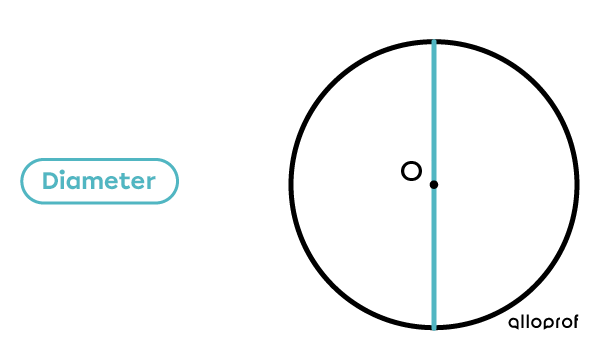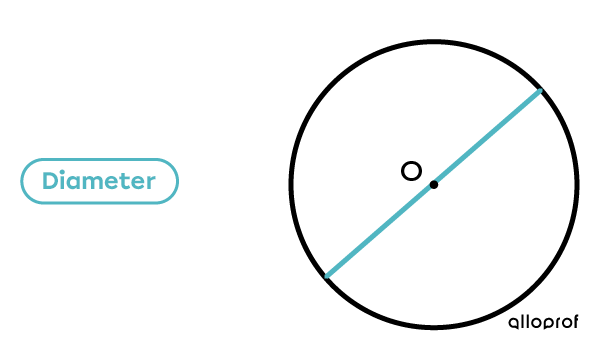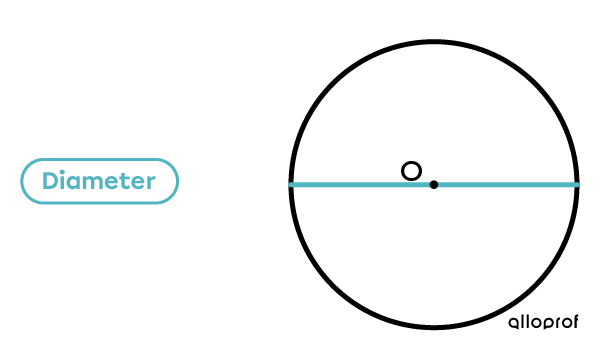
The diameter of a circle is a straight line (segment) connecting two opposite points of the circle and passing through the centre (O).
Example:
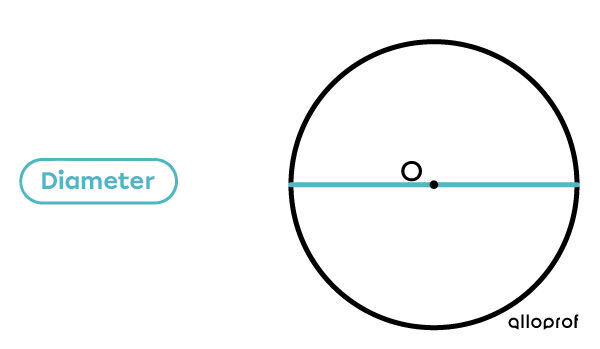
The diameter can be measured at any point on the circle.
Example:
The measurement of the diameter is always twice the radius.
This circle has a radius of |6| centimetres (cm). What is the measurement of the diameter?
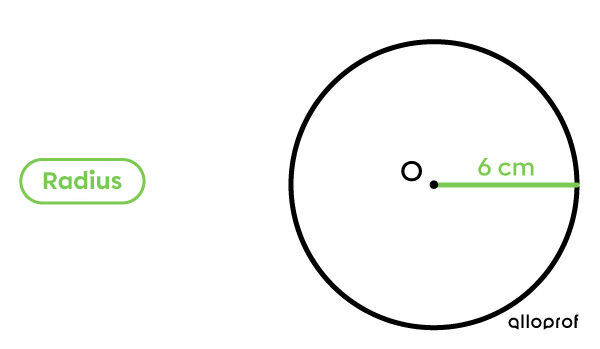
|
Multiply the measurement of the radius by |2.| |6\times2=12| |
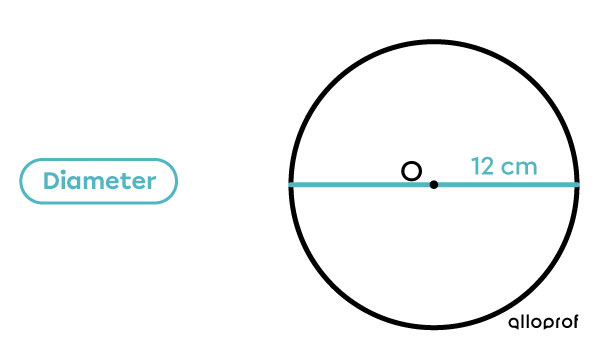 |
The circle has a diameter of |12| cm.
The central angle of a circle is an angle (|\angle|) formed by 2 radii and the vertex is located at the centre of the circle (O).
Example:
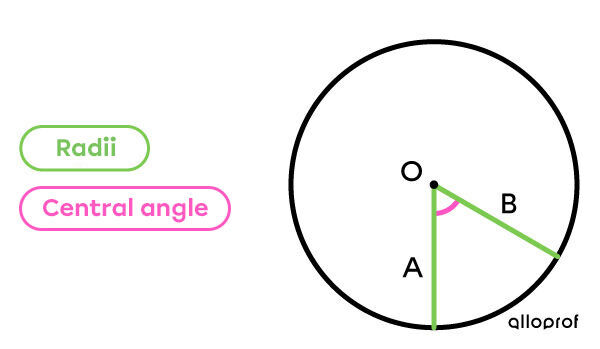
The central angle in the example is written |\angle| AOB.
The measurement of the central angle is always between |0^\circ| and |360^\circ.|
To learn how to measure an angle using a protractor, see the concept sheet Measuring Angles with a Protractor.
The disc is the area bounded by the circle.
Example: