Il est souvent possible de diviser un polygone décomposable en polygones plus simples. Cette étape permet de faciliter les calculs de son périmètre et de son aire.
Lorsqu'on travaille avec les figures décomposables, il est important de bien analyser la figure initiale afin d'en tirer un maximum d'information. Que ce soit pour reconnaitre les diverses figures utilisées ou pour déduire des mesures manquantes, la décomposition de la figure est une étape essentielle pour résoudre ce genre de problème.
-
Découper la figure décomposable en figures connues à l'aide de droites.
-
Déduire les mesures des côtés de chacune des figures connues.
-
Calculer le périmètre voulu.
-
Interpréter le périmètre obtenu afin de donner une réponse adéquate.
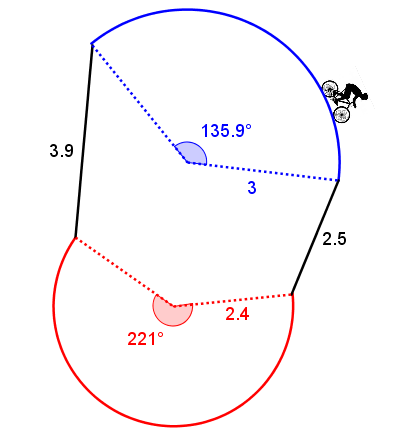
En se déplaçant à une vitesse moyenne de |18 \ \text{km/h},| combien de temps, en minutes, serait nécessaire à ce cycliste pour parcourir le circuit suivant?
Remarque : Les distances sont en km.
-
Découper la figure décomposable en figures connues à l'aide de droites
Dans le circuit qui est présenté, il s'agit de calculer les mesures des deux arcs de cercle, additionnées à celles des deux segments.
-
Déduire les mesures des côtés de chacune des figures connues ||\begin{align} \dfrac{\color{blue}{135{,}9^\circ}}{360^\circ} &=\; \dfrac{?}{\text{Circonférence}} \\ \dfrac{\color{blue}{135{,}9^\circ}}{360^\circ} &=\; \dfrac{?}{2\pi \times \color{blue}{3}} \\ \dfrac{\color{blue}{135{,}9^\circ}}{360^\circ} &\approx\; \dfrac{?}{18{,}85} \\\\ \Rightarrow\ ? &= 18{,}85 \times \color{blue}{135{,}9} \div 360 \\ ? &\approx \color{blue}{7{,}12 \ \text{km}} \end{align}||
||\begin{align} \dfrac{\color{red}{221^\circ}}{360^\circ} &=\; \dfrac{?}{\text{Circonférence}} \\ \dfrac{\color{red}{221^\circ}}{360^\circ} &=\; \dfrac{?}{2 \pi \times \color{red}{2{,}4}} \\ \dfrac{\color{red}{221^\circ}}{360^\circ} &\approx\; \dfrac{?}{15{,}08} \\\\ \Rightarrow\ ? &= 15{,}08 \times \color{red}{221} \div 360 \\ ? &\approx \color{red}{9{,}26 \ \text{km}}\end{align}||
-
Calculer le périmètre voulu ||\begin{align} P &= 2{,}5 + 3{,}9 + \color{blue}{7{,}12} + \color{red}{9{,}26} \\ &= 22{,}78 \ \text{km}\end{align}||
-
Interpréter le périmètre obtenu afin de donner une réponse adéquate
En utilisant le produit croisé, on obtient : ||\begin{align} \frac{18 \ \text{km}}{22{,}78\ \text{km}} &= \frac{60 \ \text{min}}{?}\\ \\ \Rightarrow\ ? &= 60 \times 22{,}78 \div 18 \\ &\approx 75{,}93 \ \text{min} \end{align}||Ainsi, il faudra |75{,}93 \ \text{min}| au cycliste pour faire le tour du circuit, soit |1\ \text{h}\ 15\ \text{min}\ 56\ \text{s}.|
Comme dans tout type de figure, il suffit d'additionner les mesures de chacun des côtés pour obtenir son périmètre. En le divisant de façon adéquate, on peut également déduire des mesures manquantes.
En prenant pour acquis que les mesures sont en centimètre, calcule le périmètre du polygone suivant :
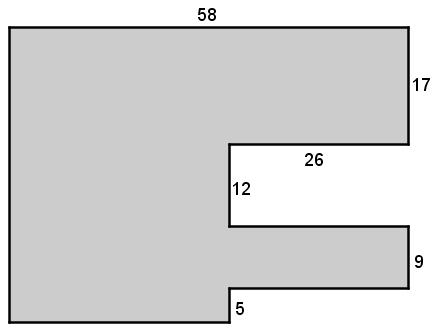
1. Découper la figure décomposable en figures connues à l'aide de droites
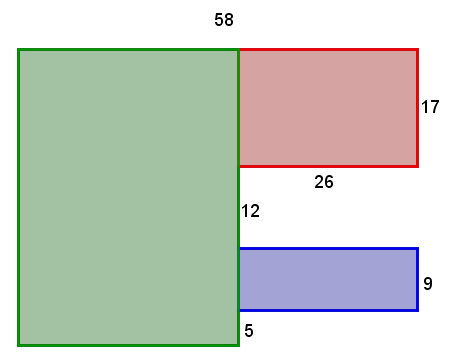
2. Déduire les mesures des côtés de chacune des figures connues
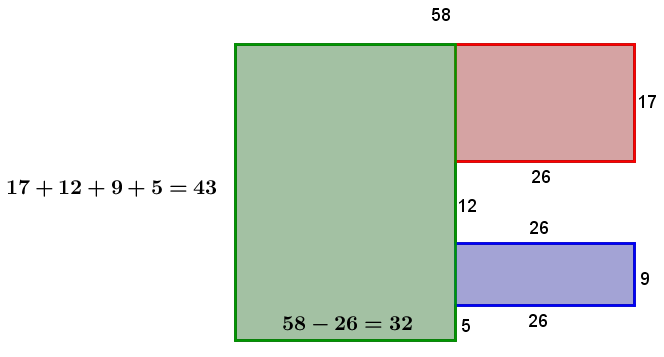
3. Calculer le périmètre voulu ||\begin{align} P &= 43 + 58 + 17 + 26 + 12 + 26 + 9 + 26 + 5 +32 \\ &= 254 \ \text{cm}\end{align}||
4. Interpréter le périmètre obtenu afin de donner une réponse adéquate.
Le périmètre de ce polygone est de |254 \ \text{cm}.|
Lorsqu'il est question de calculer l'aire d'une figure décomposable, il est nécessaire de la séparer en polygones connus. Par la suite, il suffira d'additionner ou de soustraire l'aire de tous les polygones ainsi formés. Pour déterminer l'aire de chacune des figures, il est nécessaire de se rappeler les formules d'aire des figures planes.
Une fois les formules maitrisées, on peut suivre les étapes suivantes afin de déterminer l'aire totale d'une figure décomposable.
-
Découper la figure décomposable en figures connues à l'aide de droites.
-
Déduire les mesures des côtés de chacune des figures connues.
-
Calculer l'aire de chacune des figures connues.
-
Additionner l'aire de chacune des figures connues afin d'obtenir l'aire totale.
Voici un exemple qui illustre bien chacune des étapes suggérées plus haut.
Afin de rénover la devanture de sa maison, un propriétaire veut peinturer sa porte d'entrée. Par contre, cette dernière possède trois fenêtres sur lesquelles il ne veut pas appliquer de peinture.
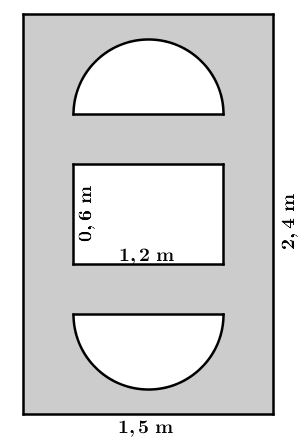
Ainsi, quelle surface de la porte, en |\text{m}^2,| sera peinturée?
Au niveau du polygone décomposable, la logique de la démarche demeure la même que pour l'aire d'une figure décomposable.
Calcule l'aire de ce polygone décomposable.
Il est à noter qu'il est possible de découper la figure initiale de plus d'une façon. Peu importe la façon dont les coupures sont faites, il faut s'assurer de pouvoir déduire les mesures des côtés des figures connues ainsi créées.
Pour valider ta compréhension de l'aire et du périmètre des figures planes de façon interactive, consulte la MiniRécup suivante :
