It is often possible to divide a decomposable polygon into simpler polygons. This step will simplify the calculations of its perimeter and area.
When working with decomposable figures, it is important to analyze the initial figure completely to obtain as much information as possible. Whether it is to identify the various figures used, or to determine missing measurements, the breakdown of the figure is an essential step in solving this kind of problem.
-
Separate the decomposable figure into known figures using lines.
-
Determine the measures of the sides of each known figure.
-
Calculate the desired perimeter.
-
Interpret the perimeter obtained to give an adequate answer.
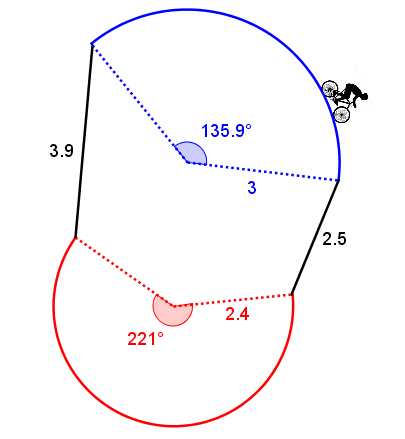
At an average speed of |18 \ \text{km/h},| how much time, in minutes, will it take the cyclist to complete the following course?
Note: The distances are in km.
-
Separate the decomposable figure into known figures using lines
In the following course, it is a question of calculating the measurements of the two arcs of a circle and adding them to those of the two segments.
-
Determine the measures of the sides of each of the known figures
||\begin{align} \dfrac{\color{blue}{135{.}9^\circ}}{360^\circ} &=\; \dfrac{?}{\text{Circumference}} \\ \dfrac{\color{blue}{135{.}9^\circ}}{360^\circ} &=\; \dfrac{?}{2\pi \times \color{blue}{3}} \\ \dfrac{\color{blue}{135{.}9^\circ}}{360^\circ} &\approx\; \dfrac{?}{18{.}85} \\\\ \Rightarrow\ ? &= 18{.}85 \times \color{blue}{135{.}9} \div 360 \\ ? &\approx \color{blue}{7{.}12 \ \text{km}} \end{align}||||\begin{align} \dfrac{\color{red}{221^\circ}}{360^\circ} &=\; \dfrac{?}{\text{Circumference}} \\ \dfrac{\color{red}{221^\circ}}{360^\circ} &=\; \dfrac{?}{2 \pi \times \color{red}{2{.}4}} \\ \dfrac{\color{red}{221^\circ}}{360^\circ} &\approx\; \dfrac{?}{15{,}08} \\\\ \Rightarrow\ ? &= 15{.}08 \times \color{red}{221} \div 360 \\ ? &\approx \color{red}{9{.}26 \ \text{km}}\end{align}||
-
Calculate the desired perimeter
||\begin{align} P &= 2{.}5 + 3{.}9 + \color{blue}{7{.}12} + \color{red}{9{.}26} \\ &= 22{.}78 \ \text{km}\end{align}|| -
Interpret the perimeter obtained to give an adequate answer
Using cross multiplication, the result is: ||\begin{align} \frac{18 \ \text{km}}{22{.}78\ \text{km}} &= \frac{60 \ \text{min}}{?}\\ \\ \Rightarrow\ ? &= 60 \times 22{.}78 \div 18 \\ &\approx 75{.}93 \ \text{min} \end{align}|| Thus, it will take |75{.}93 \ \text{min}| for the cyclist to go around the course. In other words: |1\ \text{h}\ 15\ \text{min}\ 56\ \text{s}.|
As in any type of figure, we need to add the measures of each side to obtain the perimeter. The missing measurements can be determined by dividing the shape correctly.
Assuming that the measurements are in centimetres, calculate the perimeter of the following polygon:
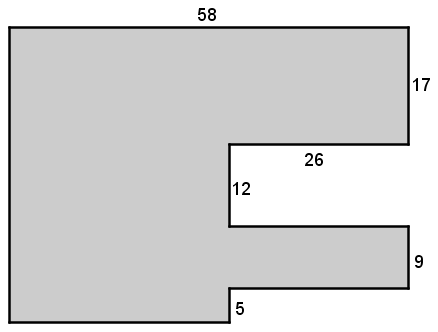
-
Separate the decomposable figure into known figures using lines
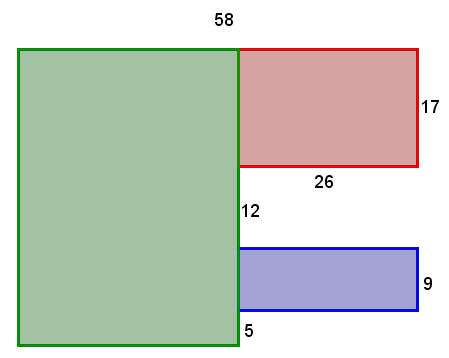
-
Determine the measurements of the sides of each known figure
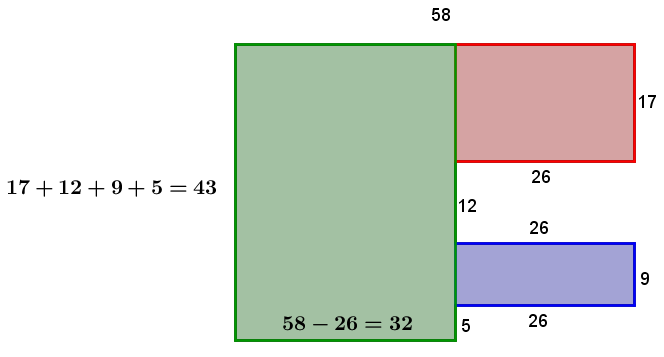
-
Calculate the desired perimeter
||\begin{align} P &= 43 + 58 + 17 + 26 + 12 + 26 + 9 + 26 + 5 +32 \\ &= 254 \ \text{cm}\end{align}|| -
Interpret the perimeter obtained to give an adequate answer.
The perimeter of the polygon is |254 \ \text{cm}.|
When calculating the area of a decomposable figure, we need to separate it into familiar polygons. Next, we add or subtract the area of all the polygons formed. To determine the area of each figure, we need to remember the area formulas of plane figures.
Once the formulas have been mastered, we can follow these steps to determine the total area of a decomposable figure.
-
Separate the decomposable figure into known figures using lines.
-
Determine the measurements of the sides of each known figure.
-
Calculate the area of each known figure.
-
Add the area of each known figure to obtain the total area.
The following example illustrates each step listed above.
A homeowner wants to paint his front door to improve the curb appeal of his house. However, the door has three windows that he does not want to paint.
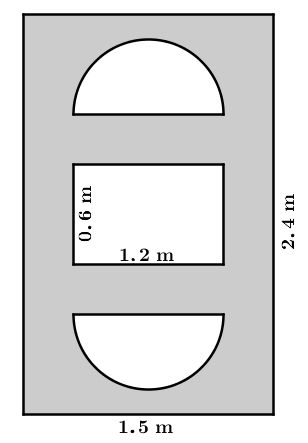
What surface area of the door, in |\text{m}^2,| will be painted?
The process for decomposable polygons is the same as for the area of decomposable figures.
Calculate the area of the following decomposable polygon.
Note: It is possible to separate the initial figure in more than one way. No matter how it is done, make sure to deduct the lengths of the figure’s known sides that are formed.
To confirm you understand the area and perimeter of flat figures, see the following interactive CrashLesson:
