<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
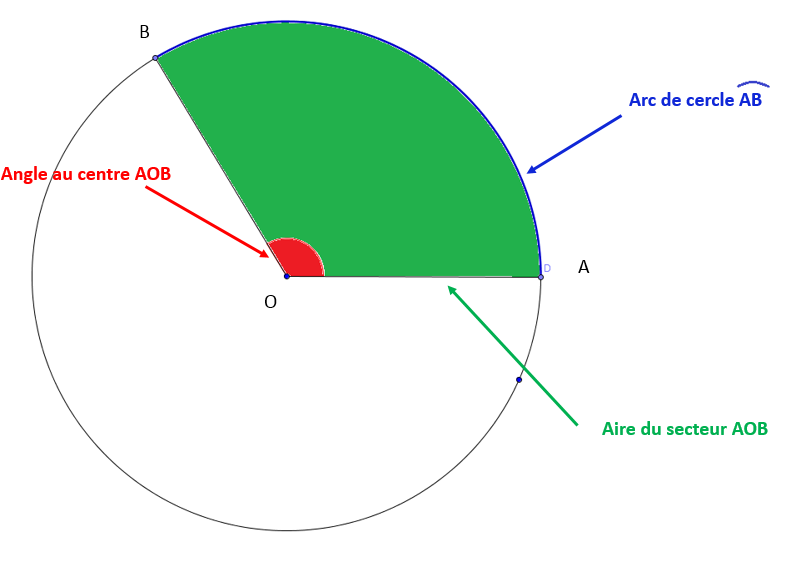
<html><body><p>Dans un cercle, un <a href="/fr/eleves/bv/mathematiques/les-angles-d-un-cercle-m1475#centre">angle au centre</a> permet de former :</p>
</body></html>
Comme l'angle au centre, l'arc de cercle et le secteur d'un disque sont liés à la même portion d'un cercle, il est possible de déterminer une de ces mesures à partir des proportions suivantes :
||\dfrac{\text{Angle au centre}}{360^\circ}=\dfrac{\text{Arc de cercle}}{\text{Circonférence}}=\dfrac{\text{Aire du secteur}}{\text{Aire du disque}}||
Un arc de cercle représente une partie de la circonférence du cercle et est formé par la rencontre de deux rayons sur la circonférence.
Si on compare le cercle à une roue de bicyclette, l'arc de cercle correspond à une section de la roue comprise entre deux rayons.
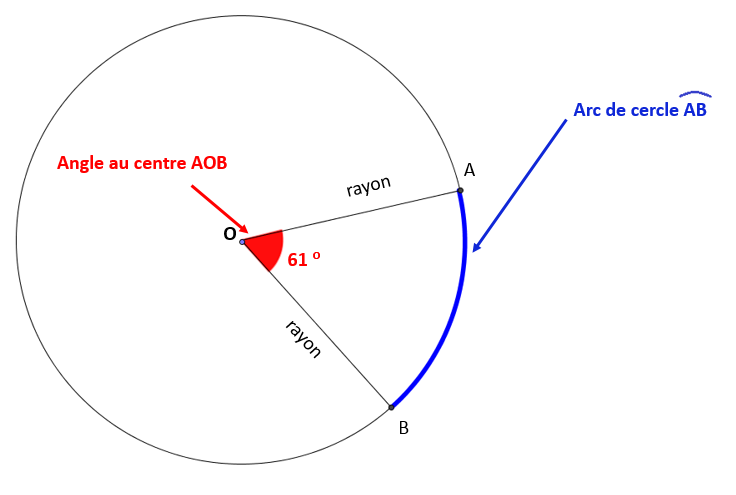
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p>L'arc de cercle représente une portion de la circonférence au même titre que l'<a href="/fr/eleves/bv/mathematiques/les-angles-d-un-cercle-m1475#centre">angle au centre</a> correspond à une portion d'un tour complet. Puisque ces portions correspondent au même rapport, on peut obtenir la longueur de l'arc de cercle en utilisant une proportion. On l'obtient en effectuant le <a href="/fr/eleves/bv/mathematiques/la-resolution-de-situations-directement-ou-invers-m1429#produit-extremes"> produit croisé</a> selon le rapport suivant :</p>
</body></html>
||\dfrac{\text{Angle au centre}}{360^\circ}=\dfrac{\text{Arc de cercle}}{\text{Circonférence}}||
Calculer la mesure de l'arc de cercle |\overset{\ \huge\frown}{AB}| inscrit par un angle au centre de |120^\circ| et dont le rayon vaut |3\ \text{cm}.|
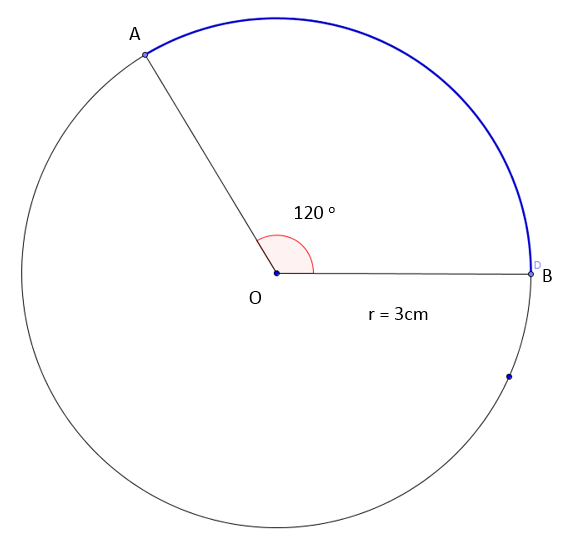
||\begin{align}\dfrac{\text{Angle au centre}}{360^\circ}&=\dfrac{\text{Arc de cercle}}{\text{Circonférence}}\\[3pt] \dfrac{120^\circ}{360^\circ}&=\dfrac{\text{m}\overset{\,\huge\frown}{AB}}{2\pi (3)}\\[3pt] \dfrac{120^\circ}{360^\circ}&=\dfrac{\text{m}\overset{\,\huge\frown}{AB}}{18{,}84\ \text{cm}}\\[5pt] \Rightarrow\ \text{m}\overset{\,\huge\frown}{AB} &= \dfrac{120^\circ\times 18{,}84\ \text{cm}}{360^\circ}= 6{,}28\ \text{cm}\end{align}||Ainsi, |\overset{\,\huge\frown}{AB}| mesure |6{,}28\ \text{cm}.|
Si un arc de cercle |\overset{\huge\frown}{CD}| mesure |15\ \text{cm}| et que la circonférence vaut |120\ \text{cm},| quelle est la mesure de l'angle au centre qui délimite cet arc de cercle?
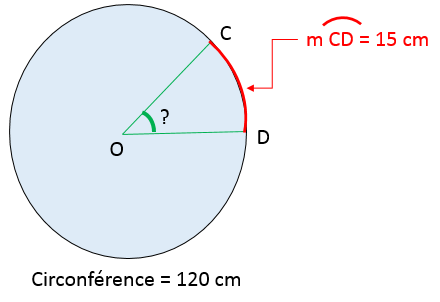
||\begin{align}\dfrac{\text{Angle au centre}}{360^\circ}&=\dfrac{\text{Arc de cercle}}{\text{Circonférence}}\\[5pt] \dfrac{\text{m}\angle DOC}{360^\circ}&=\dfrac{15\ \text{cm}}{120\ \text{cm}}\\[5pt] \Rightarrow\ \text{m}\angle DOC &= \dfrac{15\ \text{cm}\times 360^\circ}{120\ \text{cm}} = 45^\circ \end{align}||Ainsi, l'angle au centre mesure |45^\circ.|
Dans un cercle, le rapport des mesures de 2 angles au centre est égal au rapport des mesures des arcs interceptés par leurs côtés.
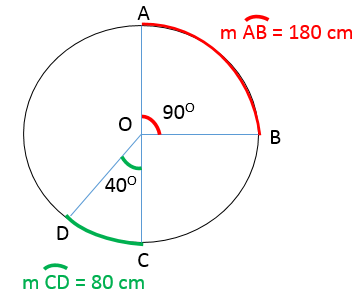
||\begin{align}\dfrac{\text{m}\angle{AOB}}{\text{m}\angle{COD}} &= \dfrac{\text{m}\overset{\,\huge\frown}{AB}}{\text{m}\overset{\huge\frown}{CD}}\\\\ \text{En effet,}\quad \dfrac{90^\circ}{40^\circ} &= \dfrac{180\ \text{cm}}{80\ \text{cm}}=2{,}25 \end{align}||
Le secteur de disque représente une partie du disque ou une section de l'aire totale de celui-ci.
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p>Il est possible de calculer l'aire d'un secteur à partir de l'<a href="/fr/eleves/bv/mathematiques/les-angles-d-un-cercle-m1475#centre">angle au centre</a> qui le forme ou de son arc de cercle.</p></body></html>
Pour trouver la superficie d'un secteur d'un disque, on peut utiliser les rapports suivants :
||\dfrac{\text{Angle au centre}}{360^\circ}=\dfrac{\text{Aire du secteur}}{\text{Aire du disque}}||
Quelle est l'aire de cette pointe de tarte si son diamètre est de |25\ \text{cm}| et que l'angle au centre correspond à |60^\circ|?
-
Calcul du rayon||\begin{align} r&=\dfrac{\text{diamètre}}{2}\\&=\dfrac{25}{2}\\ &=12{,}5\ \text{cm}\end{align}||
-
Utilisation du rapport
||\begin{align} \dfrac{\text{Angle au centre}}{360^\circ} &=\dfrac{\text{Aire du secteur}}{\text{Aire du disque}}\\\\ \dfrac{60^\circ}{360^\circ}&= \dfrac{\text{Aire du secteur}}{\pi (12{,}5)^2}\\\\ \dfrac{60^\circ}{360^\circ}&= \dfrac{\text{Aire du secteur}}{490{,}87\ \text{cm}^2}\\\\ \Rightarrow\ \text{Aire du secteur} &= \dfrac{60^\circ \times 490{,}87\ \text{cm}^2}{360^\circ}=81{,}81\ \text{cm}^2\end{align}||
Un secteur de disque vaut |60\ \text{cm}^2.| Quelle est la longueur de son arc de cercle |\overset{\,\huge\frown}{AB}| si le rayon du cercle est de |6\ \text{cm}|?
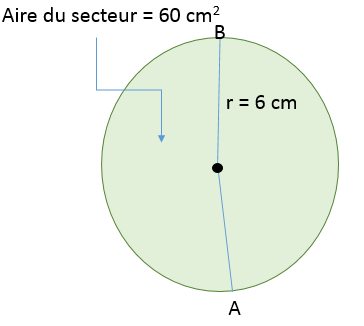
||\begin{align} \dfrac{\text{Arc de cercle}}{\text{Circonférence}}&=\dfrac{\text{Aire du secteur}}{\text{Aire du cercle}}\\[4pt] \dfrac{\text{Arc de cercle}}{2 \pi r}&=\dfrac{\text{Aire du secteur}}{\pi r^2}\\[3pt] \dfrac{\text{m}\overset{\,\huge\frown}{AB}}{2\pi (6)}&=\dfrac{60\ \text{cm}^2}{\pi (6)^2}\\[3pt] \dfrac{\text{m}\overset{\,\huge\frown}{AB}}{37{,}70\ \text{cm}}&=\dfrac{60\ \text{cm}^2}{113{,}10\ \text{cm}^2}\\[4pt] \Rightarrow\ \text{m}\overset{\,\huge\frown}{AB} &= \dfrac{37{,}70\times 60}{113{,}10}= 20\ \text{cm}\end{align}||Ainsi, |\overset{\,\huge\frown}{AB}| mesure |20\ \text{cm}.|
Dans un disque, le rapport des aires de 2 secteurs est égal au rapport des mesures des angles au centre.
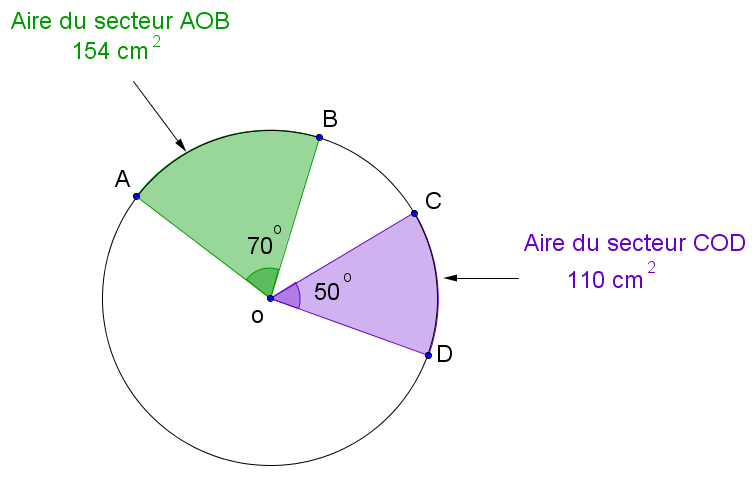
||\dfrac{\text{Aire du secteur } AOB}{\text{Aire du secteur }COD} = \dfrac{\text{m}\angle AOB}{\text{m}\angle COD}||
Pour valider ta compréhension de l'aire et du périmètre des figures planes de façon interactive, consulte la MiniRécup suivante :


