A central angle in a circle makes it possible to form the following.
Since a circle’s central angle, arc, and sector are related to the same portion of the circle, one of the measurements can be determined from the following proportions.
||\dfrac{\text{Central Angle}}{360^\circ}=\dfrac{\text{Length of the arc}}{\text{Circumference}}=\dfrac{\text{Area of the sector}}{\text{Area of the circle}}||
An arc represents a part of the circle’s circumference and is formed by the meeting of two radii on the circumference.
If we compare a circle to a bicycle wheel, the arc corresponds to the wheel sections between two spokes.
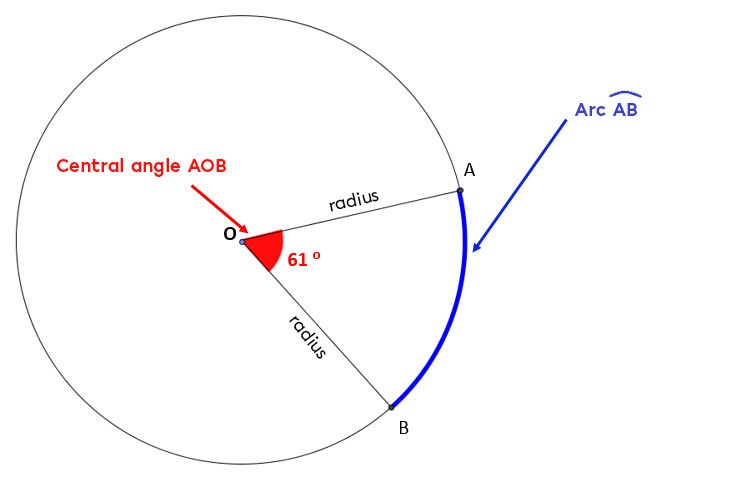
The arc of a circle represents a portion of the circumference just as the central angle corresponds to a portion of a complete turn. Since the portions correspond to the same ratio, we can obtain the length of the arc of a circle by using a proportion. The proportion is obtained by carrying out a cross multiplication according to the following ratio.
||\dfrac{\text{Central Angle}}{360^\circ}=\dfrac{\text{Length of the arc}}{\text{Circumference}}||
Calculate the length of the arc |\overset{\huge\frown}{\small{AB}}| intercepted by a central angle of |120^\circ| in a circle with a radius of |3\ \text{cm}.|

||\begin{align} \dfrac{\text{Central Angle}}{360^\circ}&=\dfrac{\text{Length of the arc}}{\text{Circumference}}\\\\ \dfrac{120^\circ}{360^\circ}&=\dfrac{m\overset{\huge\frown}{\small{AB}}}{2\pi (3)}\\\\ \dfrac{120^\circ}{360^\circ}&=\dfrac{m\overset{\huge\frown}{\small{AB}}}{18.84\ \text{cm}}\\\\ \Rightarrow m\overset{\huge\frown}{\small{AB}} &= \dfrac{120^\circ\times 18.84\text{ cm}}{360^\circ}= 6.28\ \text{cm}\end{align}||
Thus, |\overset{\huge\frown}{\small{AB}}| measures |6.28\ \text{cm}.|
If an arc |\overset{\huge\frown}{\small{CD}}| measures |15\ \text{cm}| and the circumference is |120\ \text{cm},| what is the measure of the central angle intercepting the arc of the circle?
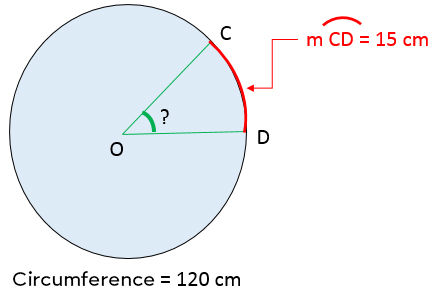
||\begin{align}\dfrac{\text{Central Angle}}{360^\circ}&=\dfrac{\text{Length of the arc}}{\text{Circumference}}\\\\
\dfrac{m\angle DOC}{360^\circ}&=\dfrac{15\ \text{cm}}{120\ \text{cm}}\\\\
\Rightarrow m\angle DOC &= \dfrac{15\ \text{cm}\times 360^\circ}{120\ \text{cm}} = 45^\circ \end{align}||
Thus, the central angle measures |45^\circ.|
In a circle, the ratio of two central angles’ measurements is equal to the ratio of the arcs’ lengths intercepted by their sides.
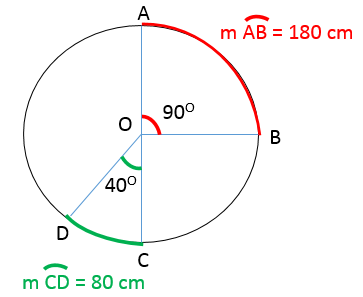
||\begin{align}\dfrac{m\angle{AOB}}{m\angle{COD}} &= \dfrac{m\overset{\huge\frown}{\small{AB}}}{m\overset{\huge\frown}{\small{CD}}}\\\\ \text{Therefore,}\quad \dfrac{90^\circ}{40^\circ} &= \dfrac{180\ \text{cm}}{80\ \text{cm}}=2.25. \end{align}||
The sector of a circle represents a part of the circle or a section of its total area.
It is possible to calculate a sector area from the central angle forming it or from its arc on the circle.
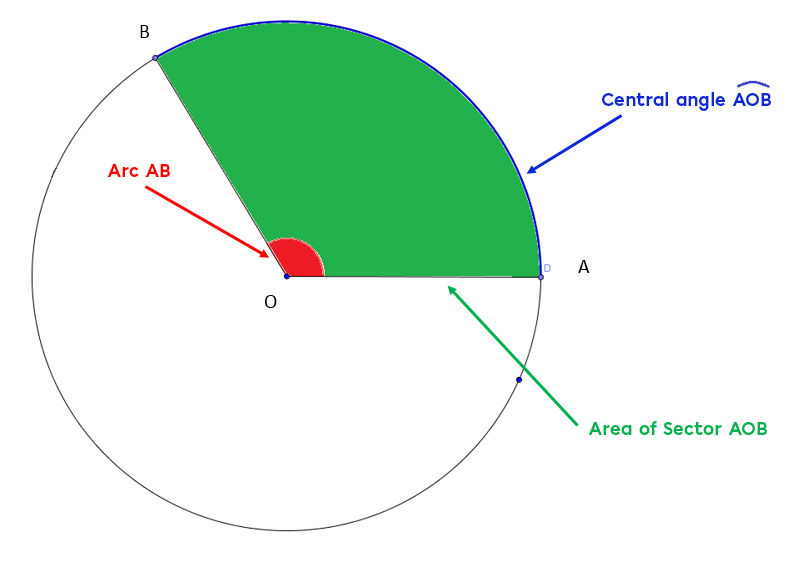
To find the area of a sector, we can use the following ratios.
||\dfrac{\text{Central Angle}}{360^\circ}=\dfrac{\text{Area of the sector}}{\text{Area of the circle}}||
What is the area of this slice of apple pie if its diameter is |25\ \text{cm}| and the central angle is |60^\circ?|
-
Find the measure of the radius
||\begin{align} r&=\dfrac{\text{Diameter}}{2}\\
&=\dfrac{25}{2}\\
&=12.5\ \text{cm}\end{align}|| -
Use the ratio
||\begin{align} \dfrac{\text{Central angle}}{360^\circ} &=\dfrac{\text{Area of the sector}}{\text{Area of the circle}}\\\\ \dfrac{60^\circ}{360^\circ}&= \dfrac{\text{Area of the sector}}{\pi (12.5)^2}\\\\ \dfrac{60^\circ}{360^\circ}&= \dfrac{\text{Area of the sector}}{490.87 \text{ cm}^2}\\\\ \Rightarrow \text{Area of the sector} &= \dfrac{60^\circ \times 490.87 \text{ cm}^2}{360^\circ}=81.81\ \text{cm}^2\end{align}||
A sector of a circle has an area of |60\ \text{cm}^2|. What is the length of its arc on the circle |\overset{\huge\frown}{\small{AB}}| if the radius of the circle is |6\ \text{cm}?|
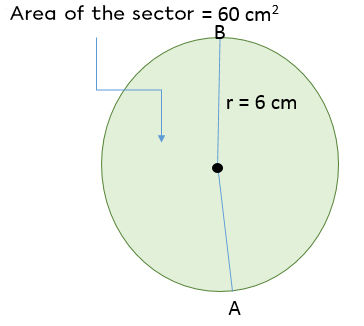
-
Use the correct ratio
||\begin{align} \dfrac{\text{Length of the arc}}{\text{Circumference}}&=\dfrac{\text{Area of the sector}}{\text{Area of the circle}}\\\\
\dfrac{\text{Length of the arc}}{2 \pi r}&=\dfrac{\text{Area of the sector}}{\pi r^2}\\\\
\dfrac{m\overset{\huge\frown}{\small{AB}}}{2\pi (6)}&=\dfrac{60\ \text{cm}^2}{\pi (6)^2}\\\\
\dfrac{m\overset{\huge\frown}{\small{AB}}}{37.70\ \text{cm}}&=\dfrac{60\ \text{cm}^2}{113.10\ \text{cm}^2}\\\\
\Rightarrow m\overset{\huge\frown}{\small{AB}} &= \dfrac{37.70\times 60}{113.10}= 20\ \text{cm}\end{align}||
Thus, |\overset{\huge\frown}{\small{AB}}| measures |20\ \text{cm}.|
In a circle, the ratio of two sectors’ areas is equal to the ratio of the measurements of their central angles.

||\dfrac{\text{Area of sector} AOB}{\text{Area of sector }COD} = \dfrac{m\angle AOB}{m\angle COD}||
Pour valider ta compréhension de l'aire et du périmètre des figures planes de façon interactive, consulte la MiniRécup suivante :


