Une chaine est une suite d'arêtes consécutives dans un graphe, un peu comme si on se promenait sur le graphe. On la désigne par les lettres des sommets qu'elle comporte.
Une chaine simple est une chaine qui ne passe pas deux fois par la même arête.
Un cycle est une chaine qui commence et se termine au même sommet.
Un cycle simple est un cycle dans lequel chaque arête est utilisée une seule fois.
La distance entre deux sommets est donnée par la longueur de la chaine la plus courte les reliant.
Il existe souvent plusieurs chaines pouvant lier deux sommets. Pour déterminer la distance entre les sommets, on choisit donc la chaine dont la longueur est la plus petite.
La distance entre les sommets A et B s’écrit |d(A,B).|
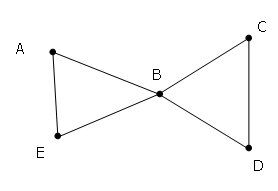
La distance entre les sommets A et C sera exprimée ainsi : ||d(A,C) = 2||
La distance est de 2, car on doit franchir au minimum deux arêtes pour passer du sommet A au sommet C.
La longueur d’une chaine est déterminée par le nombre d’arêtes qui sont parcourues dans une promenade. La même arête peut donc être répétée quand on donne la longueur d’une chaine.
La longueur est toujours égale au nombre de sommets de la chaine -1.
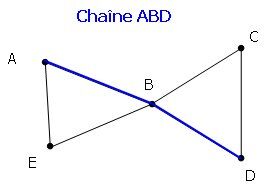
Longueur = 2
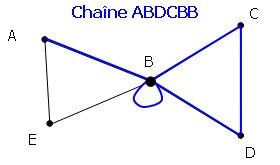
Longueur = 5
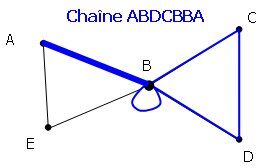
Longueur = 6
Une chaine eulérienne est une chaine qui parcourt toutes les arêtes d’un graphe connexe une et une seule fois.
On peut demander s’il est possible de parcourir tel trajet en n’empruntant jamais deux fois la même route :
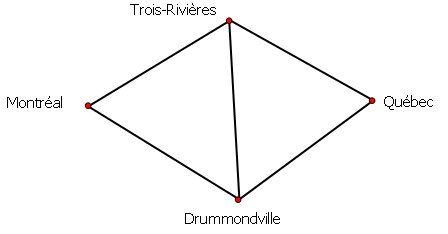
On voit que c’est possible en partant de Trois-Rivières ou Drummondville, mais pas en partant de Québec ou Montréal. Exemple : (T-Q-D-T-M-D)
Pour qu’un graphe comporte une chaine eulérienne, il faut qu’il possède 0 ou deux 2 sommets de degré impair. Dans le cas de 2 sommets de degré impair, ils seront situés au début et à la fin de la chaine.
Lorsque la chaine eulérienne est fermée, on l’appellera cycle eulérien. C’est donc une chaine qui passe par toutes les arêtes et qui revient à son point de départ.
Le cycle eulérien exige que tous les sommets du graphe soient de degré pair.
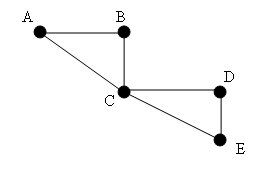
ABCDECA est un cycle eulérien.
Il passe une seule fois par toutes les arêtes du graphe et revient à son point de départ.
Une chaine ou cycle hamiltonien(ne) est une chaine ou un cycle qui passe par tous les sommets d’un graphe connexe une et une seule fois. Les chaines hamiltoniennes sont fréquemment utilisées pour résoudre des problèmes d’optimisation (par exemple, trouver le chemin le plus court. Le problème du voyageur en est un bon exemple, voir la référence plus bas).
Hormis par intuition ou par essais et erreurs, la seule règle que l’on connaisse pour déterminer la présence de cycles hamiltoniens dans un graphe connexe est la suivante.
Il y a un cycle hamiltonien dans tout graphe dont chaque sommet est relié à au moins la moitié des autres sommets.
Cette règle n’est pas restrictive, c’est-à-dire qu’on peut trouver des graphes qui ne répondent pas à cette condition et qui comportent néanmoins une chaine hamiltonienne.

Chaine hamiltonienne : FDEABCG
Cycle hamiltonien : FDEABCGF