A chain is a series of consecutive edges in a graph. They are a bit like steps, if we were to take a walk on the graph. The chain is denoted by the letters of its vertices that it visits.
A simple chain is a chain that does not pass through the same edge twice.
A cycle is a chain that begins and ends at the same vertex.
A simple cycle is a cycle where each edge is used only once.
The distance between two vertices is the length of the shortest chain connecting them.
There are often several chains connecting two vertices. To determine the distance between the vertices, choose the shortest chain.
The distance between the vertices A and B is written |d(A,B).|
The distance between vertices A and C is expressed as follows: ||d(A,C) = 2||
The distance is 2, because a minimum of two edges must be crossed to go from vertex A to vertex C.
The length of a chain is determined by the number of edges that are traveled. The same edge can be repeated when giving the length of a chain.
The length is always equal to the number of vertices of the chain -1.
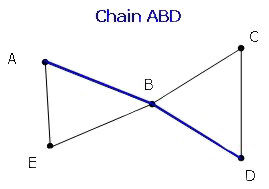
Length = 2
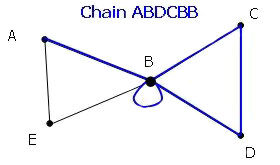
Length = 5
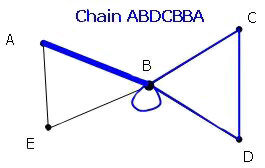
Length = 6
An Eulerian chain is a chain which travels all the edges of a connected graph only once.
Is it possible to travel such a route by never taking the same edge twice? See the following:
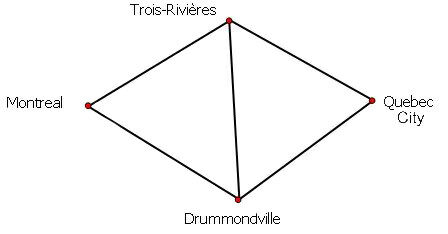
It is possible if the starting point is Trois-Rivières or Drummondville, but not if the starting point is Quebec City or Montreal. Example: T-Q-D-T-M-D
For a graph to include an Eulerian chain, it must have 0 or two vertices of an odd degree. Two vertices of an odd degree would be located at the beginning and at the end of the chain.
When an Eulerian chain is closed, it is called an Eulerian cycle. It is a chain that passes through all the edges only once and returns to the starting point.
The Eulerian cycle requires that all vertices of the graph be an even degree.
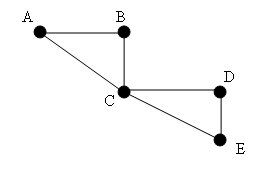
ABCDECA is an Eulerian Cycle.
It passes only once through all the edges of the graph, and begins and ends at the same vertex.
A Hamiltonian chain or cycle is a chain or a cycle that passes through all the vertices of a connected graph only once. Hamiltonian chains are frequently used to solve optimization problems (e.g., finding the shortest path. The Traveller’s Dilemma is a good example. See below).
Except by intuition or by trial and error, the only known rule for determining the presence of Hamiltonian cycles in a connected graph is:
There is a Hamiltonian cycle in any graph where each vertex is connected to at least half of the other vertices.
The rule is not restrictive. However, we can find graphs that do not meet this condition but still possess a Hamiltonian chain.

Hamiltonian chain: FDEABCG
Hamiltonian cycle: FDEABCGF