Pour permettre aux adeptes des mathématiques de résoudre les différents problèmes, une quantité de formules et de théorèmes ont été découverts au fil de l'histoire. Dans plusieurs cas, ces théorèmes étaient d'abord des conjectures.
Une conjecture est un énoncé mathématique que l'on accepte comme vrai, mais dont on ne connait pas la valeur de vérité puisqu'il n'a jamais été démontré ou réfuté.
De façon générale, le raisonnement associé à la validation d'une conjecture peut se présenter de trois façons différentes.
Peu importe la forme adoptée, le même genre de démarche peut être utilisé dans chacun des cas.
Concernant le cas de la démonstration, la conjecture est déjà émise dans le problème. Ainsi, il ne reste qu'à la valider à l'aide de différents exemples.
Démontrer que dans les polyèdres seulement, lorsque l'on soustrait |2| à la somme du nombre de faces et de sommets, on obtient le nombre d'arêtes du prisme initial.
Exemple 1 - cube
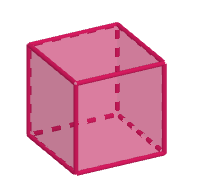
||\begin{align}\text{nb de sommets}&=\,8\\\text{nb de faces}&=\,6\\\text{nb d'arêtes}&=12\end{align}||
Ainsi,||\begin{alignat}{14}\text{nb de sommets}&+\text{nb de faces }&&-&&\;2&&\stackrel{?}{=}\text{nb d'arêtes}\\\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!8&+\quad\;\;\,6&&-&&\;2&&\stackrel{?}{=}\quad\;12\\&&&&&12&&=\quad\;12\end{alignat}||
Exemple 2 - prisme à base pentagonale
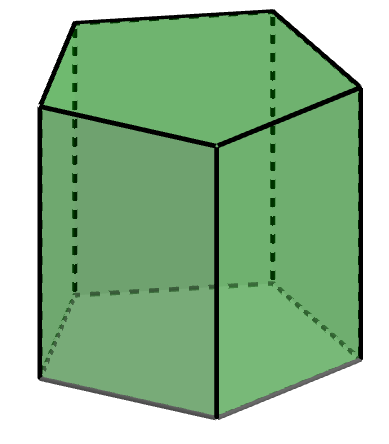
||\begin{align}\text{nb de sommets}&=10\\\text{nb de faces}&=\,7\\\text{nb d'arêtes}&=15\end{align}||
Ainsi,||\begin{alignat}{14}\text{nb de sommets}&+\text{nb de faces }&&-&&\;2&&\stackrel{?}{=}\text{nb d'arêtes}\\\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!10&+\quad\;\;\,7&&-&&\;2&&\stackrel{?}{=}\quad\;15\\&&&&&15&&=\quad\;15\end{alignat}||
Exemple 3 - pyramide à base triangulaire
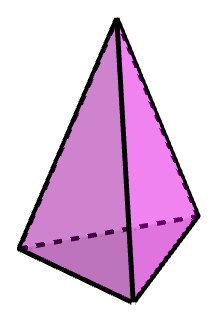
||\begin{align}\text{nb de sommets}&=4\\\text{nb de faces}&=4\\\text{nb d'arêtes}&=6\end{align}||
Ainsi,||\begin{alignat}{14}\text{nb de sommets}&+\text{nb de faces }&&-&&\;2&&\stackrel{?}{=}\text{nb d'arêtes}\\\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!4&+\quad\;\;\,4&&-&&\;2&&\stackrel{?}{=}\quad\;6\\&&&&&\;6&&=\quad\;6\end{alignat}||
Au fil du temps, certaines conjectures sont mathématiquement prouvées et acceptées dans la communauté mathématique. Lorsque c'est le cas, il passe au stade de « relation » ou de « théorème ».
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p><span>Dans le cas présent, il s'agit de <a href="/fr/eleves/bv/mathematiques/la-relation-d-euler-m1242">la relation d'Euler</a>. </span></p>
</body></html>
Au niveau secondaire, la démonstration d'une conjecture par le biais d'un minimum de trois exemples valides est généralement acceptée. Par contre, pour détruire une conjecture, soit démontrer qu'elle est fausse, il suffit d'un seul contre-exemple.
Une fois de plus, on peut procéder en illustrant notre démarche par le biais d'au moins trois exemples de différentes natures. Dans l'exemple qui suit, les polygones seront abordés. Ainsi, les exemples inclus dans la démarche ne seront pas tous des carrés ou des rectangles.
Détermine si la conjecture suivante est vraie ou fausse.
« Quand on double la mesure d'un côté d'un polygone, alors on double la mesure de son aire. »
Exemple 1 - rectangle
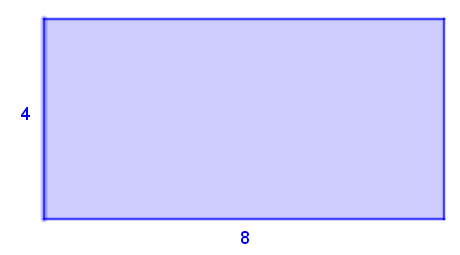
||\begin{align}\text{Aire}_\text{rectangle}&=b\times h\\&=8\times4\\&=32\text{ unités}^2\end{align}||
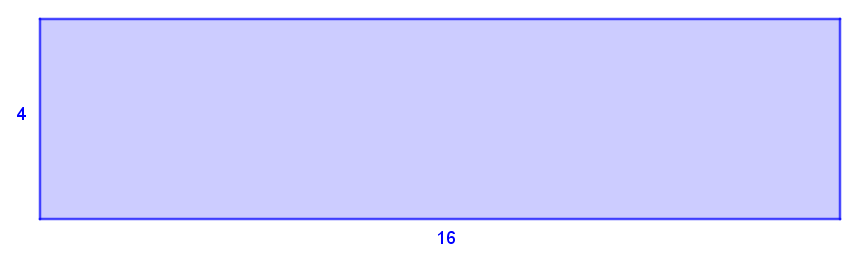
||\begin{align}\text{Aire}_\text{rectangle}&=b\times h\\&=16\times4\\&=64\text{ unités}^2\end{align}||
Puisque | 32 \times 2 = 64,| l'énoncé est vrai selon cet exemple.
Exemple 2 - triangle
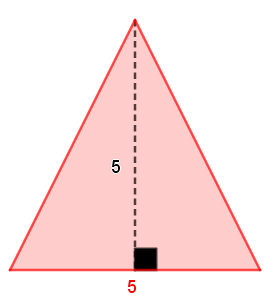
||\begin{align}\text{Aire}_\text{triangle}&=\dfrac{b\times h}{2}\\&=\dfrac{5\times5}{2}\\&=12{,}5\text{ unités}^2\end{align}||
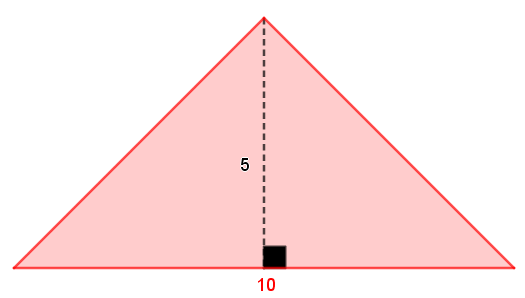
||\begin{align}\text{Aire}_\text{triangle}&=\dfrac{b\times h}{2}\\&=\dfrac{10\times5}{2}\\&=25\text{ unités}^2\end{align}||
Puisque |12{,}5 \times 2 = 25,| l'énoncé est toujours vrai.
Exemple 3 - pentagone régulier
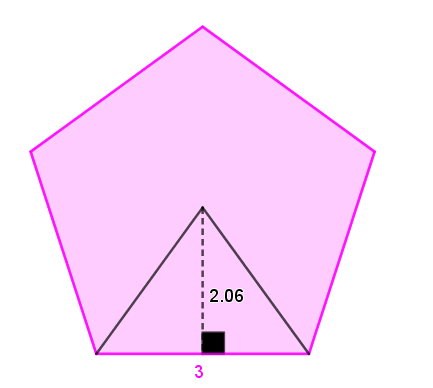
||\begin{align}\text{Aire}_\text{pentagone}&=\dfrac{c\times a\times n}{2}\\&=\dfrac{3\times2{,}
06\times5}{2}\\&=15{,}45\text{ unités}^2\end{align}||
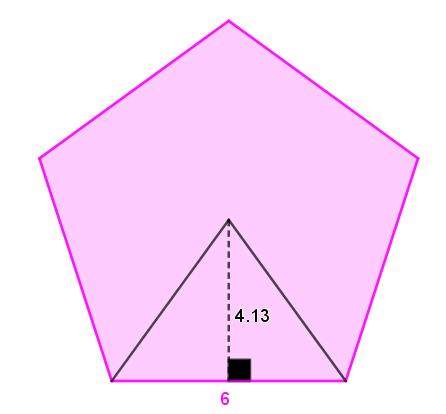
||\begin{align}\text{Aire}_\text{pentagone}&=\dfrac{c\times a\times n}{2}\\&=\dfrac{6\times4{,}
13\times5}{2}\\&=61{,}95\text{ unités}^2\end{align}||
Puisque |15{,}45 \times 2 \neq 61{,}95,| l'énoncé est faux.
Compléter la conjecture
Ainsi, la conjecture proposée était fausse étant donné que le pentagone régulier est un contre-exemple de l'affirmation initiale.
Selon les propriétés du pentagone régulier, le fait de modifier la mesure d'un côté a une influence sur la mesure de l'apothème. Ainsi, ce n'est plus simplement une mesure de segment qui est modifiée, mais deux d'entre eux.
Pour formuler une conjecture, l'idée de procéder avec au moins trois exemples est un bon point de départ.
Fait à noter, lorsqu'on cherche à dégager une généralité, il est toujours idéal de prendre des exemples qui sont « consécutifs ». Dans le cas présent, des polygones à |5|, |6| et |7| côtés seront analysés.
Une fois les calculs faits, l'analyse des résultats est de mise afin d'en déduire une généralité.
Que peut-on dégager comme conjecture qui met en lien le nombre de côtés d'un polygones ainsi que sa quantité de diagonales?
Exemple 1 - pentagone
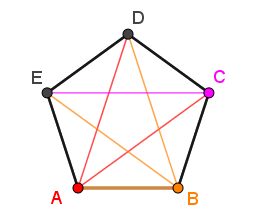
Par définition d'une diagonale, |2| diagonales peuvent être issues de chacun des sommets.
Pour déterminer le nombre total de diagonales, on doit faire la somme des « nouvelles » de chacun des sommets.||\begin{alignat}{13}\text{nb de diagonales}&=\color{red}{\text{ A }}&&+\color{orange}{\text{ B }}&&+\color{fuchsia}{\text{ C}}\\&=\;\color{red}{2}&&+\;\color{orange}{2}&&+\;\color{fuchsia}{1}\\&=\;5\end{alignat}||
Exemple 2 - hexagone
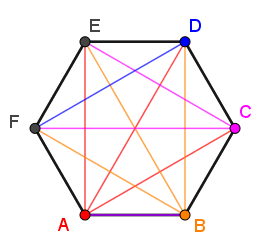
Dans le cas d'un hexagone, |3| diagonales peuvent être tracées à partir de chacun des sommets.
On effectue la même méthode qu'au premier exemple.||\begin{alignat}{14}\text{nb de diagonales}&=\color{red}{\text{ A }}&&+\color{orange}{\text{ B }}&&+\color{fuchsia}{\text{ C }}&&+\color{blue}{\text{ D}}\\&=\;\color{red}{3}&&+\;\color{orange}{3}&&+\;\color{fuchsia}{2}&&+\;\color{blue}{1}\\&=\;9\end{alignat}||
Exemple 3 - heptagone
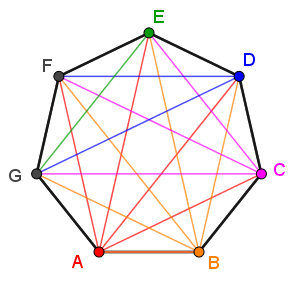
En ce qui concerne l'heptagone, chaque sommet possède |4| diagonales.
Ainsi, on a l'équation suivante.||\begin{alignat}{15}\text{nb de diagonales}&=\color{red}{\text{ A }}&&+\color{orange}{\text{ B }}&&+\color{fuchsia}{\text{ C }}&&+\color{blue}{\text{ D }}&&+\color{darkgreen}{\text{ E}}\\&=\;\color{red}{4}&&+\;\color{orange}{4}&&+\;\color{fuchsia}{3}&&+\;\color{blue}{2}&&+\;\color{darkgreen}{1}\\&=\,14\end{alignat}||
Dégager une généralité (formule)
D'un exemple à l'autre, c'est d'abord le nombre de côtés du polygone qui a été modifié. Ainsi, on peut poser l'équation suivante.||n = \text{nb de côtés du polygone}||Par la suite, les diagonales étaient tracées à partir du sommet |A| et à chaque fois, le nombre de diagonales de ce sommet correspondaient à l'équation suivante.||\text{nb de côtés} - 3 = n-3||Puisque le nombre total de diagonales semble augmenter de façon exponentielle, on va utiliser la multiplication entre ces deux expressions algébriques et analyser le tout.
Puisque |n \times(n-3) = n^2 - 3n,| alors on a : ||\begin{align}\text{pentagone}&=5\ \text{diagonales}\\&\stackrel{?}{=}(5)^2-3(5)&&\text{avec}\ n=5\\&\stackrel{?}{=}10\\\\\text{hexagone}&=9\ \text{diagonales}\\&\stackrel{?}{=}(6)^2-3(6)&&\text{avec}\ n=6\\&\stackrel{?}{=}18\\\\\text{heptagone}&=14\ \text{diagonales}\\&\stackrel{?}{=}(7)^2-3(7)&&\text{avec}\ n=7\\&\stackrel{?}{=}28\end{align}||Au final, on s'aperçoit que le nombre de diagonales trouvées selon les dessins correspond à la moitié du résultat obtenu par la formule |n^2 - 3n.|
Formuler la conjecture
Ainsi, on peut en déduire que dans un polygone, le nombre de diagonales peut être calculées selon la formule suivante.||\text{nb de diagonales} = \dfrac{n^2-3n}{2}||
Bien entendu, le tout requiert une certaine dose de déduction et un bon sens de l'observation au niveau arithmétique. Par contre, le simple fait de construire trois exemples apporte déjà beaucoup de contenu à une telle démarche.