Many formulas and theorems have been discovered throughout history to help mathematicians solve various problems. In many cases, these theorems began as conjectures.
A conjecture is a mathematical statement that is accepted as true, but whose truth value is unknown because it has never been proven or disproven.
Generally speaking, the reasoning associated with validating a conjecture may be presented in three different ways:
Whatever form is chosen, the same sort of approach can be used in each case.
With proofs, the conjecture is already stated in the problem. All that needs to be done is validate it using different examples.
Prove (for polyhedrons only) that if |2| is subtracted from the sum of the number of faces and vertices, the number of edges of the original prism is obtained.
Example 1 - Cube
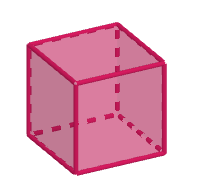
||\begin{align}\text{no. of vertices}&=\,8\\\text{no. of faces}&=\,6\\\text{no. of edges}&=12\end{align}||
Therefore,||\begin{alignat}{14}\text{no. of vertices}&+\text{no. of faces }&&-&&\;2&&\stackrel{?}{=}\text{no. of edges}\\\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!8&+\quad\;\;\,6&&-&&\;2&&\stackrel{?}{=}\quad\;12\\&&&&&12&&=\quad\;12\end{alignat}||
Example 2 - Pentagonal-based prism
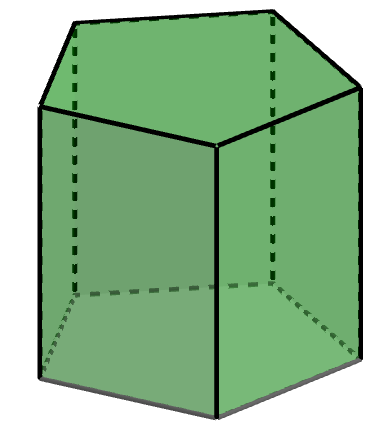
||\begin{align}\text{no. of vertices}&=10\\\text{no. of faces}&=\,7\\\text{no. of edges}&=15\end{align}||
Therefore,||\begin{alignat}{14}\text{no. of vertices}&+\text{no. of faces }&&-&&\;2&&\stackrel{?}{=}\text{no. of edges}\\\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!10&+\quad\;\;\,7&&-&&\;2&&\stackrel{?}{=}\quad\;15\\&&&&&15&&=\quad\;15\end{alignat}||
Example 3 - Triangular-based pyramid
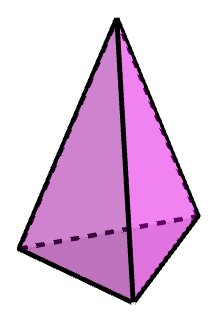
||\begin{align}\text{no. of vertices}&=4\\\text{no. of faces}&=4\\\text{no. of edges}&=6\end{align}||
Therefore,||\begin{alignat}{14}\text{no. of vertices}&+\text{no. of faces }&&-&&\;2&&\stackrel{?}{=}\text{no. of edges}\\\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!4&+\quad\;\;\,4&&-&&\;2&&\stackrel{?}{=}\quad\;6\\&&&&&\;6&&=\quad\;6\end{alignat}||
Over time, certain conjectures are proven mathematically and accepted by the mathematical community. When this is the case, the conjecture moves from being a "relationship" to becoming a "theorem".
This present conjecture is Euler’s formula.
At the secondary school level, proving a conjecture by showing a minimum of three valid examples is generally accepted as enough evidence. On the other hand, to disprove a conjecture, that is, to show that it is false, only one counterexample is needed.
Once again, we can illustrate our approach by using at least three examples of different nature. Polygons are the focus of the following example. The examples included in the approach will not all be squares or rectangles.
Determine if the following conjecture is true or false.
“When the length of one side of a polygon is doubled, its area is also doubled.”
Example 1 - Rectangle

||\begin{align}\text{Area}_\text{rectangle}&=b\times h\\&=8\times4\\&=32\text{ units}^2\end{align}||
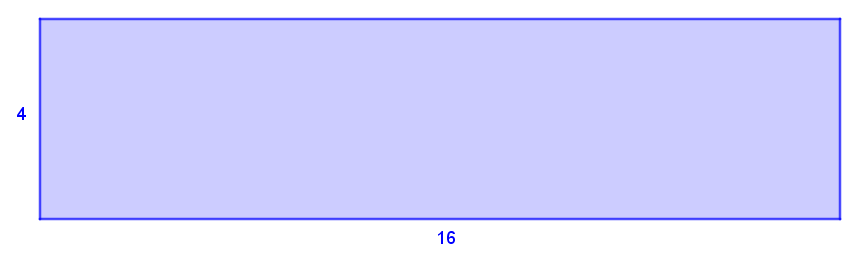
||\begin{align}\text{Area}_\text{rectangle}&=b\times h\\&=16\times4\\&=64\text{ units}^2\end{align}||
Since | 32 \times 2 = 64,| according to this example, the conjecture holds true.
Example 2 - Triangle
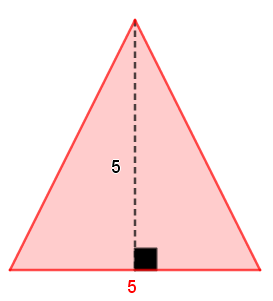
||\begin{align}\text{Area}_\text{triangle}&=\dfrac{b\times h}{2}\\&=\dfrac{5\times5}{2}\\&=12.5\text{ units}^2\end{align}||
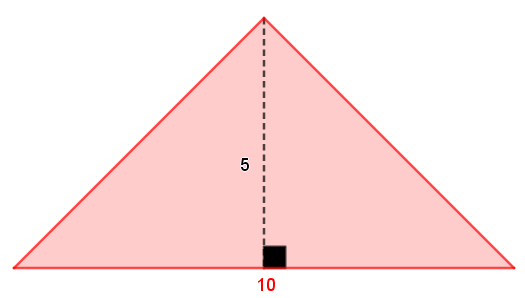
||\begin{align}\text{Area}_\text{triangle}&=\dfrac{b\times h}{2}\\&=\dfrac{10\times5}{2}\\&=25\text{ units}^2\end{align}||
Since |12.5 \times 2 = 25,| the conjecture still holds true.
Example 3 - Regular Pentagon
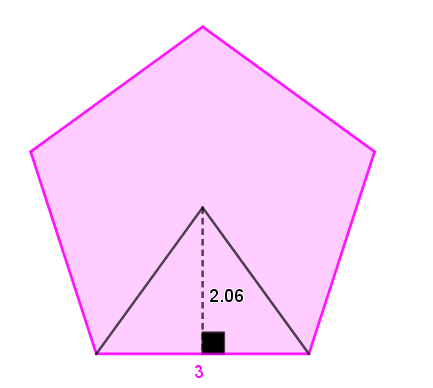
||\begin{align}\text{Area}_\text{pentagon}&=\dfrac{s\times a\times n}{2}\\&=\dfrac{3\times2.
06\times5}{2}\\&=15.45\text{ units}^2\end{align}||
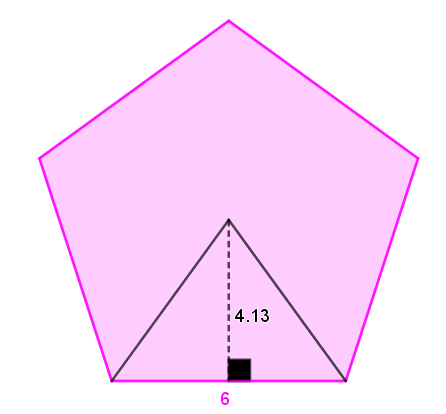
||\begin{align}\text{Area}_\text{pentagon}&=\dfrac{s\times a\times n}{2}\\&=\dfrac{6\times4.
13\times5}{2}\\&=61.95\text{ units}^2\end{align}||
Since |15.45 \times 2 \neq 61.95,| the conjecture is false.
Complete the conjecture
Therefore, the proposed conjecture is false, since the regular pentagon is a counterexample of the original assertion.
In accordance with the properties of a regular pentagon, changing the measure of one side affects the measure of the apothem. This means that rather than just one segment being changed, two of them are modified.
To formulate a conjecture, a good starting point is to use at least three examples.
It's worth noting that when we're trying to identify a relationship, it's ideal to use “consecutive” examples. In this case, we will analyze polygons with |5,| |6| and |7| sides.
Once the calculations are done, the outcomes are analyzed to deduce a general relationship.
What conjecture can be made about the relationship between the number of sides of a polygon and its number of diagonals?
Example 1 - Pentagon
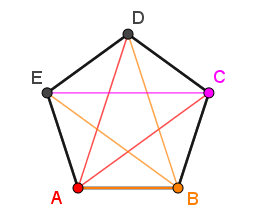
According to the definition of a diagonal, |2| diagonals can be drawn from each of the vertices.
To determine the total number of diagonals, add the "new" diagonals for each of the vertices:||\begin{alignat}{13}\text{no. of diagonal lines}&=\color{red}{\text{ A }}&&+\color{orange}{\text{ B }}&&+\color{fuchsia}{\text{ C}}\\&=\;\color{red}{2}&&+\;\color{orange}{2}&&+\;\color{fuchsia}{1}\\&=\;5\end{alignat}||
Example 2 - Hexagon
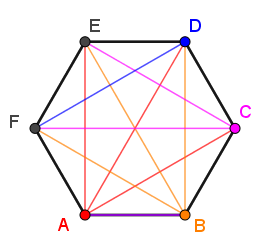
For a hexagon, |3| diagonal lines can be drawn from each vertex.
Just like in the first example:||\begin{alignat}{14}\text{no. diagonal lines}&=\color{red}{\text{ A }}&&+\color{orange}{\text{ B }}&&+\color{fuchsia}{\text{ C }}&&+\color{blue}{\text{ D}}\\&=\;\color{red}{3}&&+\;\color{orange}{3}&&+\;\color{fuchsia}{2}&&+\;\color{blue}{1}\\&=\;9\end{alignat}||
Example 3 - Heptagon
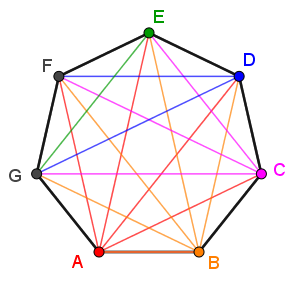
For a heptagon, |4| diagonal lines can be drawn from each vertex.
So we have the following equation:||\begin{alignat}{15}\text{no. of diagonal lines}&=\color{red}{\text{ A }}&&+\color{orange}{\text{ B }}&&+\color{fuchsia}{\text{ C }}&&+\color{blue}{\text{ D }}&&+\color{darkgreen}{\text{ E}}\\&=\;\color{red}{4}&&+\;\color{orange}{4}&&+\;\color{fuchsia}{3}&&+\;\color{blue}{2}&&+\;\color{darkgreen}{1}\\&=\,14\end{alignat}||
Identify a relationship (formula)
From one example to another, the number of sides in the polygon changed. Therefore, let||n = \text{no. of sides of the polygon}.||Next, diagonals were drawn from vertex |A,| and each time, the number of diagonal lines from this vertex corresponded to||\text{no. of sides} - 3 = n-3.||Since the total number of diagonal lines seems to increase exponentially, multiply these two algebraic expressions and analyze the situation.
Since |n \times (n-3) = n^2 - 3n|:||\begin{align}\text{pentagon}&=5\ \text{diagonals}\\&\stackrel{?}{=}(5)^2-3(5)&&\text{where}\ n=5\\&\stackrel{?}{=}10\\\\\text{hexagon}&=9\ \text{diagonals}\\&\stackrel{?}{=}(6)^2-3(6)&&\text{where}\ n=6\\&\stackrel{?}{=}18\\\\\text{heptagon}&=14\ \text{diagonals}\\&\stackrel{?}{=}(7)^2-3(7)&&\text{where}\ n=7\\&\stackrel{?}{=}28\end{align}||Ultimately, the number of diagonals found in the drawings corresponds to half the result obtained from the formula |n^2 - 3n.|
Formulate the conjecture
Therefore, it can be deduced that in a polygon, the number of diagonals can be calculated using the following formula:||\text{no. of diagonal lines} = \dfrac{n^2-3n}{2}||
Of course, all this requires a certain amount of deduction and a good sense of observation when it comes to arithmetic. However, the simple fact of constructing three examples provides a great deal of information to use in this way.