Dans le langage mathématique, le concept d'orthogonalité fait référence à des objets mathématiques qui forment un angle de |90^\circ|. Dans le cas des projections en géométrie, on peut associer cet angle particulier à celui qui est formé par le champ vision et l'objet regardé.
La projection orthogonale est la représentation sur papier d'un objet en trois dimensions selon les différentes vues de cet objet.
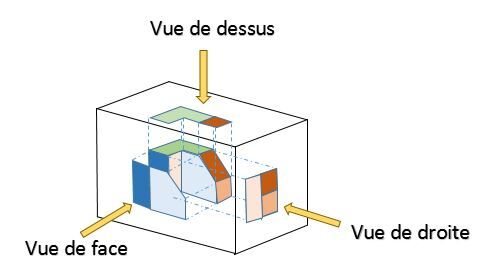
L'exemple suivant permet d'illustrer cette projection.

Cette perspective ne rend généralement pas compte de l'aspect de profondeur des différents solides observés. Cet effet de trois dimensions est annulé par la perpendicularité existant entre le champ de vision et l'objet observé.
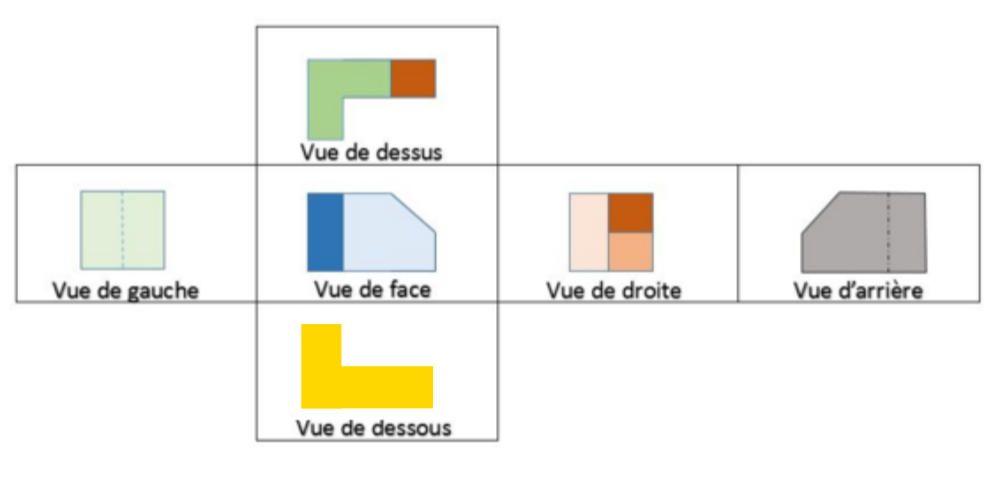
Il existe au total six différentes vues.
Une vue correspond à la figure plane obtenue sur papier selon la position de l'observateur par rapport à l'objet.
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p>Contrairement aux <a href="/fr/eleves/bv/mathematiques/les-projections-paralleles-perspectives-cavalie-m1276">projections parallèles</a> ou <a href="/fr/eleves/bv/mathematiques/les-projections-centrales-a-un-ou-deux-points-de-m1277">centrales</a> où un seul dessin suffit pour représenter l'objet à trois dimensions, il faut plusieurs projections orthogonales (plusieurs représentations de diverses vues) du même objet pour pouvoir déduire son allure en trois dimensions.</p>
<p>Les représentations d'un objet à l'aide de ce type de projection montrent habituellement trois vues : la vue de face, celle d'un des côtés et celle de dessus. Ceci correspond d'ailleurs au nombre maximal de vues qu'une personne peut apercevoir en même temps dans la réalité, sans possibilité de prendre l'objet dans ses mains pour pouvoir le tourner et le regarder sous tous ses angles.</p>
</body></html>
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p>Parfois, la projection orthogonale de certaines faces de <a href="/fr/eleves/bv/mathematiques/les-solides-decomposables-et-tronques-m1404">solides décomposables</a> peut aider à déterminer des mesures pertinentes pour le calcul de l'aire totale des solides.<br>
<br>
Finalement, la projection orthogonale est souvent utilisée en dessin technique afin de représenter les différentes vues d'un objet. </p>
</body></html>