In mathematical language, the concept of orthogonality refers to mathematical objects that form a |90^\circ| angle. For geometrical projections, it is associated with the angle formed by the field of view and the object being viewed.
An orthogonal projection is the representation on paper of a three-dimensional object using the different views of that object.
The following example illustrates this type of projection.
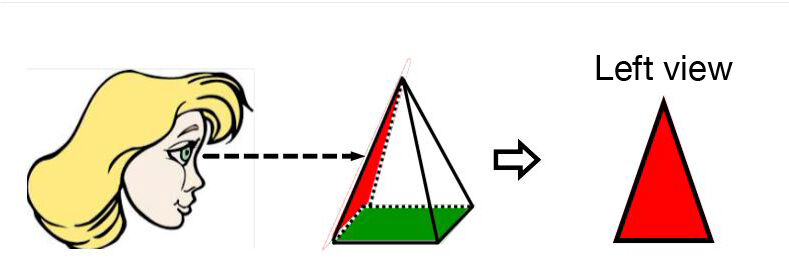
This perspective generally does not show the depth aspect of the various solids being observed. The three-dimensional effect is cancelled out by the right angle that exists between the field of vision and the object observed.
There are a total of six different views.
A view is the flat figure on paper that matches the view seen by the observer's position relative to the object.
Unlike parallel or central projections, where a single drawing is enough to represent the object in three dimensions, it takes several orthogonal projections (multiple representations of various views) of the same object to understand its appearance in three dimensions.
Representing an object with this type of projection usually involves showing three views: the front view, the side view, and the top view. This also corresponds to the maximum number of views that a person can see at the same time in reality. This does not take into account the possibility of a person taking the object in their hands and being able to turn it and look at it from all angles.
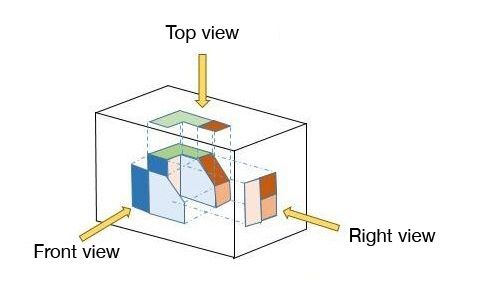
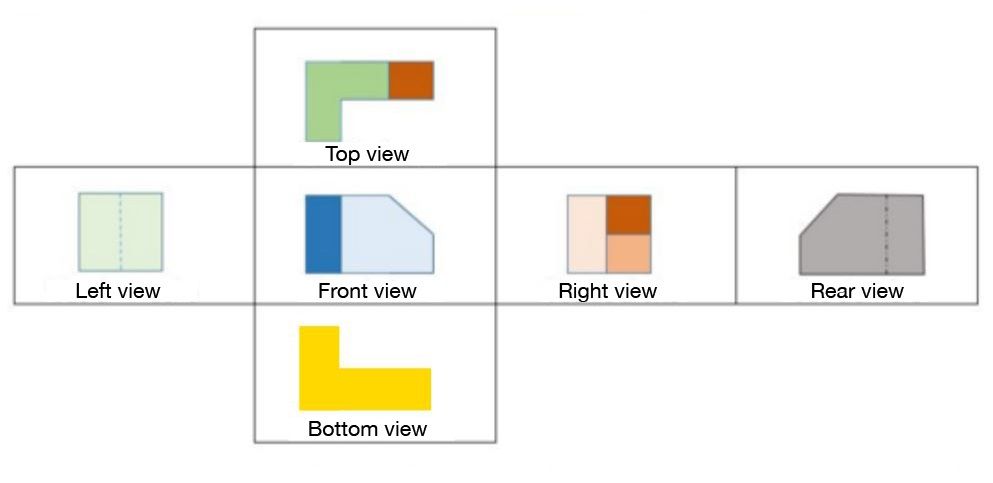
Sometimes the orthogonal projection of certain faces of solids that can be decomposed can help determine the relevant measurements for calculating the total area of solids.
To summarize, orthogonal projections are often used in technical drawings to represent different views of an object.