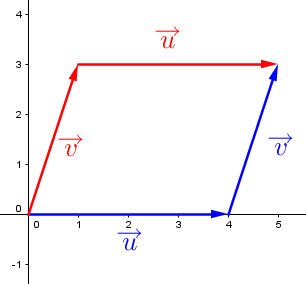
On obtient cette propriété ainsi : ||\begin{align} \overrightarrow{u} + \overrightarrow{v} &= \overrightarrow{AB} + \overrightarrow{BC} \\
&= \overrightarrow{AD} + \overrightarrow{DC}\\
&=\overrightarrow{v} + \overrightarrow{u}\end{align}||
||\color{Red}{\overrightarrow{u}+(\overrightarrow{v}+\overrightarrow{w}) = (\overrightarrow{u}+\overrightarrow{v})+\overrightarrow{w}}||On obtient cette propriété en utilisant les vecteurs |\overrightarrow{AB}, \overrightarrow{BC}| et |\overrightarrow{CD}| et la relation de Chasles.||\begin{align}(\overrightarrow{AB} + \overrightarrow{BC})+\overrightarrow{CD} &= \overrightarrow{AC}+\overrightarrow{CD} \\
&= \overrightarrow{AD}\end{align}||On effectue un calcul similaire en déplaçant les parenthèses.||\begin{align} \overrightarrow{AB} + (\overrightarrow{BC}+\overrightarrow{CD}) &= \overrightarrow{AB}+\overrightarrow{BD} \\
&= \overrightarrow{AD}\end{align}||Et ainsi le résultat est démontré.
Additif :||\color{Red}{\overrightarrow{u}+\overrightarrow{0}=\overrightarrow{u}}||Les composantes du vecteur |\overrightarrow{u}| sont |(a,b)| et celles du vecteur |\overrightarrow{0}| sont |(0,0)|.
Ainsi : ||\begin{align} \overrightarrow{u} + \overrightarrow{0} &= (a,b)+(0,0)\\
&= (a+0,b+0)\\
&=(a,b) \\
&= \overrightarrow{u}\end{align}||
Multiplicatif :||\color{Red}{1\overrightarrow{u}=\overrightarrow{u}}||Les composantes du vecteur |\overrightarrow{u}| sont |(a,b)|.
Ainsi : ||\begin{align}1 \times \overrightarrow{u}&=1 \times (a,b) \\
&= (1a,1b) \\
&=(a,b) \\
&= \overrightarrow{u}\end{align}||
||\color{Red}{\overrightarrow{u}+(-\overrightarrow{u})=\overrightarrow{0}}||Les composantes du vecteur |\overrightarrow{u}| sont |(a,b)| et celles du vecteur |-\overrightarrow{u}| sont |(-a,-b)|.
Alors : ||\begin{align}\overrightarrow{u} + (-\overrightarrow{u})&=(a,b)+(-a,-b) \\
&= (a-a,b-b) \\
&= (0,0) \\
&= \overrightarrow{0}\end{align}||
||\color{Red}{k(c\overrightarrow{u})=(kc)\overrightarrow{u}}||Les composantes du vecteur |\overrightarrow{u}| sont |(a,b)|.
Alors : ||\begin{align}k(c \overrightarrow{u}) &= k(c(a,b))\\
&=k(ca,cb)\\
&=(kca,kcb)\\
&=(kc)(a,b) \\
&= (kc)\overrightarrow{u}\end{align}||
||\color{Red}{k(\overrightarrow{u}+\overrightarrow{v})=k\overrightarrow{u}+k\overrightarrow{v}}||Les composantes du vecteur |\overrightarrow{u}| sont |(a,b)| et celles du vecteur |\overrightarrow{v}| sont |(c,d).|
Alors :||\begin{align}k(\overrightarrow{u}+\overrightarrow{v}) &= k((a,b)+(c,d)) \\
&= k(a+c,b+d) \\
&= (k(a+c),k(b+d))\\
&=(ka+kc,kb+kd) \\
&= (ka,kb)+(kc,kd)\\
&=k\overrightarrow{u}+k\overrightarrow{v}\end{align}||
||\color{Red}{(k+c)\overrightarrow{u}=k\overrightarrow{u}+c\overrightarrow{u}}||Les composantes du vecteur |\overrightarrow{u}| sont |(a,b).|
Alors :||\begin{align} (k+c)\overrightarrow{u} &=(k+c)(a,b) \\
&=((k+c)a,(k+c)b) \\
&= (ka+ca,kb+cb) \\
&= (ka,kb)+(ca+cb)\\
&=k(a,b)+c(a,b) \\
&= k\overrightarrow{u}+c\overrightarrow{u}\end{align}||
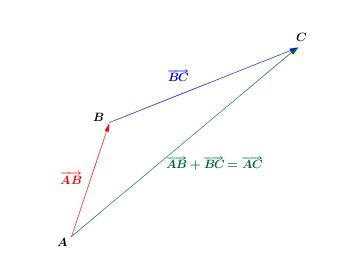
Pour cette relation |A|, |B| et |C| représente des points dans le plan cartésien.||\color{Red}{\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}}||
||\color{Red}{ \overrightarrow{u} \cdot (\overrightarrow{v} + \overrightarrow{w}) = \overrightarrow{u} \cdot \overrightarrow{v} + \overrightarrow{u} \cdot \overrightarrow{w}}||
Soit |\overrightarrow{u}=(a,b)|, |\overrightarrow{v}=(c,d)| et |\overrightarrow{w}=(e,f)|.
Ainsi,
||\begin{align}\overrightarrow{u} \cdot (\overrightarrow{v} + \overrightarrow{w}) &= (a,b) \cdot ((c,d)+(e,f))\\
&= (a,b) \cdot (c+e,d+f) \\
&=(a(c+e)+b(d+f))\\
&=(ac+ae+bd+bf)\\
&=(ac+bd)+(ae+bf) \\
&= (a,b) \cdot (c,d) + (a,b) \cdot (e,f)\\
&= \overrightarrow{u} \cdot \overrightarrow{v} + \overrightarrow{u} \cdot \overrightarrow{w}\end{align}||
Soit |\overrightarrow{u}=(a,b)|, |\overrightarrow{v}=(c,d)| des vecteurs, |k_1| et |k_2| des scalaires.||\color{Red}{k_1 \overrightarrow{u} \cdot k_2 \overrightarrow{v}=(k_1k_2)\overrightarrow{u} \cdot \overrightarrow{v}}||
||\begin{align}k_1 \overrightarrow{u} \cdot k_2 \overrightarrow{v} &= k_1(a,b) \cdot k_2(c,d)\\
&= (k_1a,k_1b) \cdot(k_2c,k_2d)\\
&= k_1k_2ac+k_1k_2bd\\
&=(k_1k_2)(ac+bd)\\
&= (k_1k_2)(a,b) \cdot (c,d)\\
&=(k_1k_2)\overrightarrow{u} \cdot \overrightarrow{v}\end{align}||
Pour valider ta compréhension à propos des vecteurs de façon interactive, consulte la MiniRécup suivante :
