Les relations métriques dans le cercle

​​​​Les relations métriques dans un cercle sont des phrases mathématiques exprimant un lien entre les diverses grandeurs dans un cercle.

Dans un même cercle ou dans deux cercles isométriques, deux cordes isométriques sont situées à la même distance du centre et réciproquement.

Dans le cercle ci-dessous :

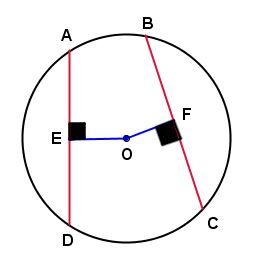
• si la mesure de la corde |\overline{AD}| est égale à la mesure de la corde |\overline{BC},| alors la mesure du segment |\overline{EO}| est égale à la mesure du segment |\overline{FO};|

• si la mesure du segment |\overline{EO}| est égale à la mesure du segment |\overline{FO}|, alors la mesure de la corde |\overline{AD}| est égale à la mesure de la corde |\overline{BC}.|

On peut résumer ceci de la façon suivante.

Si |\mathrm{m}\overline{AD} = \mathrm{m}\overline{BC},| alors |\mathrm{m}\overline{EO} = \mathrm{m}\overline{FO}.|

Si |\mathrm{m}\overline{EO} = \mathrm{m}\overline{FO},| alors |\mathrm{m}\overline{AD} = \mathrm{m}\overline{BC}.|

Tout diamètre perpendiculaire à une corde partage cette corde et chacun des arcs qu'elle sous-tend en deux parties isométriques.

Dans le cercle-ci-dessous :

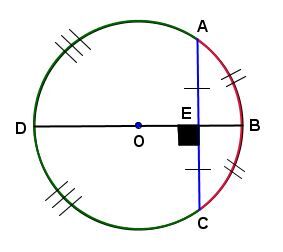
• si la mesure du segment |\overline{AE}| est égale à la mesure du segment |\overline{CE}|, alors la mesure de l'arc |\overset{\huge\frown}{AB}| est égale à la mesure de l'arc |\overset{\huge\frown}{BC​}| et la mesure de l'arc |\overset{\huge\frown}{AD}| est égale à la mesure de l'arc |\overset{\huge\frown}{DC};|

• si la mesure de l'arc |\overset{\huge\frown}{AB}| est égale à la mesure de l'arc |\overset{\huge\frown}{BC}| et que la mesure de l'arc |\overset{\huge\frown}{AD}| est égale à la mesure de l'arc |\overset{\huge\frown}{DC},| alors la mesure du segment |\overline{AE}| est égale à la mesure du segment |\overline{CE}.|

On peut résumer ceci de la façon suivante.

Si |\mathrm{m}\overline{AE} = \mathrm{m}\overline{CE},| alors |\mathrm{m}\overset{\huge\frown}{{AB}} = \mathrm{m}\overset{\huge\frown}{{BC}}| et |\mathrm{m}\overset{\huge\frown}{{AD}} = \mathrm{m}\overset{\huge\frown}{{DC}}.|

Si |\mathrm{m}\overset{\huge\frown}{{AB}} = \mathrm{m}\overset{\huge\frown}{{BC}}| et |\mathrm{m}\overset{\huge\frown}{{AD}} = \mathrm{m}\overset{\huge\frown}{{DC}},| alors |\mathrm{m}\overline{AE} = \mathrm{m}\overline{CE}.|

Dans le cercle ci-dessous :

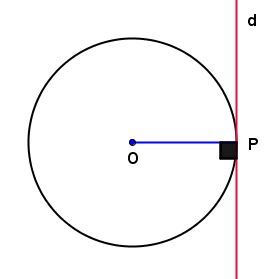
• si la droite |d| passe par l'extrémité |P| du rayon |\overline{OP}| et qu'elle est perpendiculaire à ce rayon, alors la droite |d| est tangente au cercle de centre |O;|

• si la droite |d| est tangente au cercle au cercle de centre |O,| alors la droite |d| est perpendiculaire au rayon |\overline{OP}.|

On peut résumer ceci de la façon suivante.

Si |d \perp \overline{OP},| alors |d| est tangente au cercle.

Si |d| est tangente au cercle, alors |d \perp \overline{OP}.|

Deux parallèles sécantes ou tangentes à un cercle, interceptent sur le cercle deux arcs isométriques.

Dans le cercle ci-dessous :

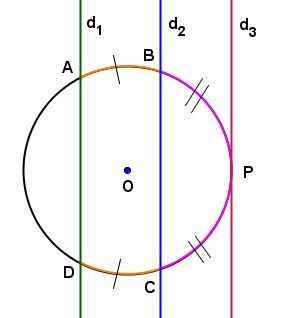
• si les droites |d_1| et |d_2| sont parallèles, alors la mesure de l'arc |\overset{\huge\frown}{{AB}}| est égale à la mesure de l'arc |\overset{\huge\frown}{{DC}};|

• si les droites |d_2| et |d_3| sont parallèles, alors la mesure de l'arc |\overset{\huge\frown}{{BP}}|est égale à la mesure de l'arc |\overset{\huge\frown}{{CP}}.|

On peut résumer ceci de la façon suivante.

Si |d_1 \parallel d_2,| alors |\mathrm{m} \overset{\huge\frown}{{AB}} = \mathrm{m} \overset{\huge\frown}{{DC}}.|

Si |d_2 \parallel d_3,| alors |\mathrm{m} \overset{\huge\frown}{{BP}} = \mathrm{m} \overset{\huge\frown}{{CP}}.|

Une tangente à un cercle est un droite qui rencontre un cercle en un seul point.

Un angle inscrit a pour mesure la moitié de celle de l'arc compris entre ses côtés.

Dans le cercle ci-dessous :

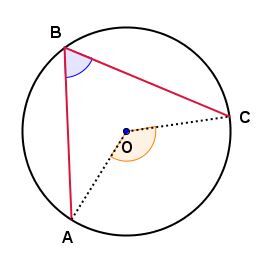
La mesure de l'angle |ABC| est égale à la moitié de la mesure de l'angle |AOC.|

On peut résumer ceci de la façon suivante. ||\begin{align} \mathrm{m}\angle ABC &=  \dfrac{\mathrm{m}\overset{\huge\frown}{{AC}}}{2} \\
&= \dfrac{\mathrm{m}\angle{AOC}}{2}\end{align}||Exemple : ||\begin{align} \mathrm{m}\angle AOC &= 120° \\ \Rightarrow\ \mathrm{m}\angle ABC &= 60°\end{align}||

L'angle dont le sommet est situé entre le cercle et son centre a pour mesure la demi-somme des mesures des arcs compris entre ses côtés prolongés.

Dans le cercle ci-dessous :

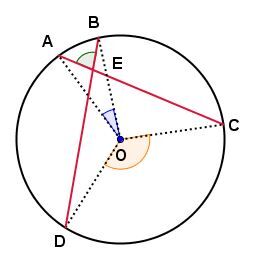
• la mesure de l'angle | AEB| est égale à la moitié de la somme des mesures des arcs |\overset{\huge\frown}{{AB}}| et |\overset{\huge\frown}{{CD}};|

• la mesure de l'angle |AEB| est égale à la moitié de la somme des mesures des angles |AOB| et |COD.|

On peut résumer ceci de la façon suivante.

|\mathrm{m}\angle AEB = \dfrac{\mathrm{m}\overset{\huge\frown}{{AB}} + \mathrm{m}\overset{\huge\frown}{{CD}}}{2}|

|\mathrm{m}\angle AEB = \dfrac{\mathrm{m}\angle AOB + \mathrm{m}\angle COD}{2}|

L'angle dont le sommet est situé à l'extérieur d'un cercle a pour mesure la demi-différence des mesures des arcs compris entre ses côtés.

Dans le cercle ci-dessous :

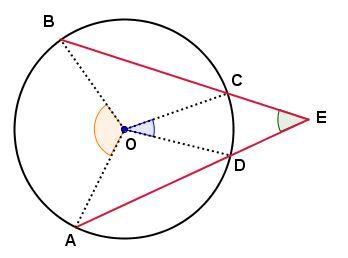
• la mesure de l'angle |\angle AEB| est égale à la moitié de la différence des mesures des arcs |\overset{\huge\frown}{{AB}}| et |\overset{\huge\frown}{{CD}};|

• la mesure de l'angle |\angle AEB| est égale à la moitié de la différence des mesures des angles |\angle AOB| et |\angle COD.|

On peut résumer ceci de la façon suivante.

|\mathrm{m}\angle AEB = \dfrac{\mathrm{m}\overset{\huge\frown}{{AB}} - \mathrm{m}\overset{\huge\frown}{{CD​​}}}{2}|

|\mathrm{m}\angle AEB = \dfrac{\mathrm{m}\angle AOB - \mathrm{m}\angle COD}{2}|

Si, d'un point |P| extérieur à un cercle de centre |O|, on mène deux tangentes aux points |A| et |B| du cercle, alors la droite |OP| est la bissectrice de l'angle |APB| et |\mathrm{m}\overline{PA}=\mathrm{m}\overline{PB}.|

Dans le cercle ci-dessous :

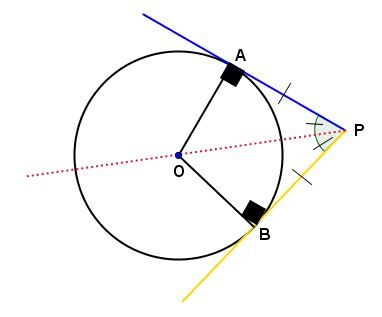
Puisque les demis-droites |PA| et |PB| sont tangentes au cercle de centre |O,| les angles |APO| et |BPO| sont égaux puisque |PO| est la bissectrice de l'angle |APB| et que les mesures de |\overline{PA}| et de |\overline{PB}| sont égales.

On peut résumer ceci de la façon suivante.

|\mathrm{m}\overline{PA}=\mathrm{m}\overline{PB}|

|\mathrm{m}\angle APO=\mathrm{m}\angle BPO= \dfrac{\mathrm{m}\angle APB}{2}|

Si, d'un point |P| extérieur au cercle de centre |O,| on mène deux sécantes |PB| et |PD,| alors le produit de |\mathrm{m}\overline{PA}| et de |\mathrm{m}\overline{PB}| est égal au produit de |\mathrm{m}\overline{PC}| et de |\mathrm{m}\overline{PD}.|

Dans le cercle ci-dessous, on peut dire ceci. ||\mathrm{m}\overline{PA}\times \mathrm{m}\overline{PB} = \mathrm{m}\overline{PC}\times \mathrm{m}\overline{PD}||

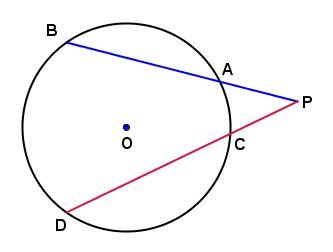
Supposons les mesures suivantes. ||\begin{align} \mathrm{m}\overline{PA}& =2{,}7\ \mathrm{cm} \\
\mathrm{m}\overline{PC}&=2{,}4\ \mathrm{cm} \\
\mathrm{m}\overline{CD}&=4{,}8\ \mathrm{cm}\end{align}||On obtient ceci. ||\begin{align} 2{,}7\times \mathrm{m}\overline{PB} &= 2{,}4\times (2{,}4 + 4{,}8) \\ \mathrm{m}\overline{PB} &=  \dfrac{2{,}4\times7{,}2}{2{,}7}\\ \mathrm{m}\overline{PB}&= 6{,}4\ \mathrm{cm}\end{align}||La mesure de |\overline{AB}| est donc de |6{,}4 - 2{,}7 = 3{,}7\ \mathrm{cm}.|

Si, d'un point |P| extérieur à un cercle, on mène une sécante |PB| et une tangente |PC,| alors le produit de |\mathrm{m}\overline{PA}| et de |\mathrm{m}\overline{PB}| est égal au carré de |\mathrm{m}\overline{PC}.|

Dans le cercle ci-dessous, on peut dire ceci. ||\mathrm{m}\overline{PA}\times \mathrm{m}\overline{PB}=(\mathrm{m}\overline{PC})^{2}||

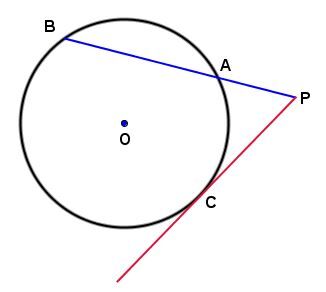
Supposons les mesures suivantes. ||\begin{align} \mathrm{m}\overline{PA}&=0{,}8\ \mathrm{cm}\\
\mathrm{m}\overline{AB}&=1{,}8\ \mathrm{cm}\end{align}||On obtient ceci.||\begin{align}0{,}8\times (0{,}8 + 1{,}8)&=(\mathrm{m}\overline{PC})^{2} \\
\sqrt{2{,}08}&=\mathrm{m}\overline{PC}\\
1{,}44\ \mathrm{cm} &\approx \mathrm{m}\overline{PC}\end{align}||

Lorsque deux cordes se coupent dans un cercle, le produit des mesures des segments de l'une égale le produit des mesures des segments de l'autre.

Dans le cercle ci-dessous, on peut dire ceci. ||\mathrm{m}\overline{AE}\times \mathrm{m}\overline{CE}=\mathrm{m}\overline{BE}\times \mathrm{m}\overline{DE}||

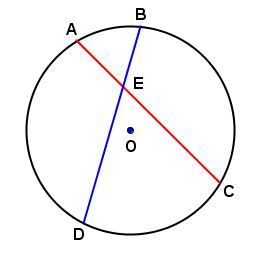
Supposons les mesures suivantes. ||\begin{align}\mathrm{m}\overline{AE}&=0{,}3\ \mathrm{cm}\\
\mathrm{m}\overline{CE}&=1{,}2\ \mathrm{cm}\\
\mathrm{m}\overline{DE}&=1{,}3\ \mathrm{cm}\end{align}||On obtient ceci. ||\begin{align}0{,}3\times 1{,}2&=\mathrm{m}\overline{BE}\times 1{,}3\\
0{,}28\ \mathrm{cm} &\approx \mathrm{m}\overline{BE}\end{align}||