Un système d'équations peut être représenté par un graphique ou par des tables de valeurs. Ces représentations peuvent aussi nous permettre de résoudre le système.
Lorsqu'un système d'équations est représenté par un graphique, il suffit de regarder le point d'intersection des droites afin de déterminer le couple solution |(x, y)|.
Soit le graphique suivant :
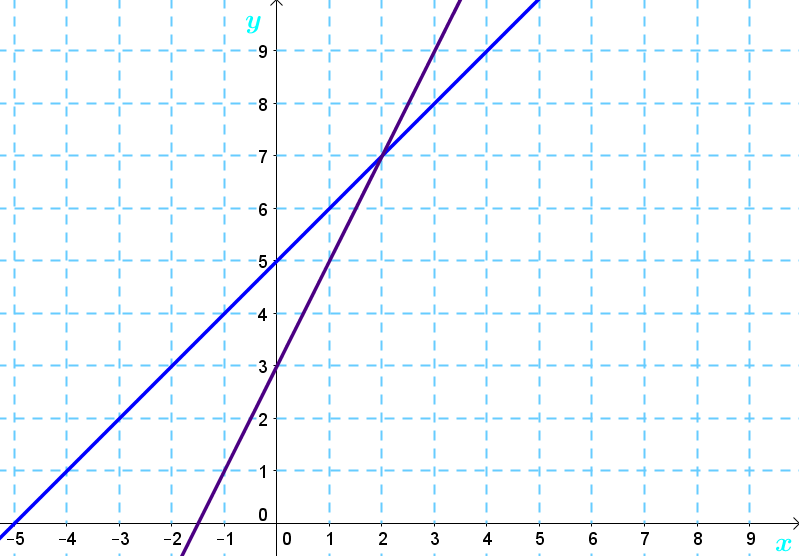
On remarque que les droites se rencontrent au point |(2, 7)|, ce qui est le couple solution du système d'équations.
Attention, dans le cas d'un système d'équations semi-linéaires, il est possible d'avoir deux solutions pour un même système d'équations.
Soit le graphique suivant :
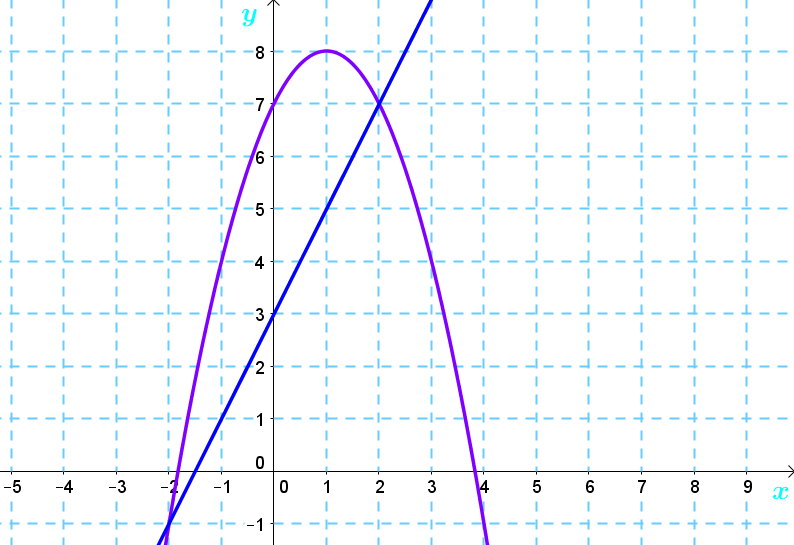
La parabole et la droite se croisent en 2 points, il y a donc 2 couples solutions soient les couples |(-2,-1)| et |(2,7)|.
Lorsqu'on dispose des tables de valeurs pour un système d'équations, il suffit de comparer les tables de valeurs de chaque droite afin de déterminer le couple solution |(x, y)|. Il faut donc trouver une valeur de la variable indépendante pour laquelle les valeurs de la variable dépendante sont identiques.
Soit les 2 tables de valeurs suivantes.
Table de valeurs de la 1re équation :
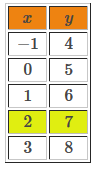
Table de valeurs de la 2e équation :
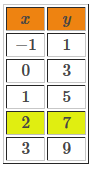
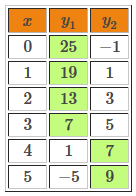
Pour une même valeur de |x| |(x=2),| on trouve une valeur de |y| identique ||y=7|| dans les deux tables de valeurs. Le couple solution de ce système d'équations est donc : |(2,7).|
Les tables de valeurs des équations du système ne seront pas toujours fournies. Dans ces cas, il faudra construire les tables de valeurs à l'aide des équations du système.
Soit le système d'équations suivant où |y_1| correspond à la variable dépendante de la première équation et |y_2| celle de la deuxième équation.
||\begin{cases}y_1=-6x+25\\ y_2=2x-1\end{cases}||
Afin de trouver le couple solution de ce système, on peut construire une table de valeurs à l'aide des deux équations. Pour facilité le repérage du couple solution, il est préférable de construire un table de valeurs « double ».
On remarque dans cette table de valeurs que, lorsque |x| prend des valeurs inférieures ou égales à |3,| on a |\color{green}{y_1}>y_2,| alors que lorsque |x| prend des valeurs supérieures ou égales à |4,| on a |y_1<\color{green}{y_2}.| La valeur recherchée se retrouve donc entre |3| et |4.| Pour trouver le couple solution, on devra diminuer le pas de variation de la façon suivante.
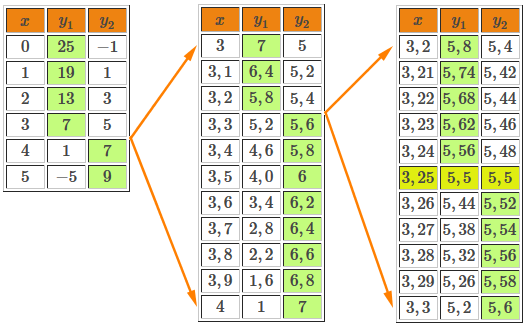
Dans cet exemple, on a dû diminuer le pas de variation deux fois pour trouver le couple solution. On remarque que pour une même valeur de |x| |(x=3{,}25),| on obtient des valeurs identiques pour les variables dépendantes des deux équations |(y=5{,}5).| Le couple solution de ce système est donc |(3{,}25;5{,}5).|
Pour valider ta compréhension à propos de la résolution de systèmes d'équations de façon interactive, consulte la MiniRécup suivante.
