Voici les étapes à suivre pour tracer une fonction en escalier (partie entière) dans un graphique.
-
Trouver le point de départ
Le point le plus important du graphique d’une fonction partie entière est l’extrémité fermée (point plein) du segment qu'il y a lieu d'appeler le segment de base. -
Trouver la longueur des segments (marches)
Une fois que l’on a bien positionné l’extrémité fermée du segment de base, il faut trouver la longueur des segments. La longueur des segments est donnée par la valeur du paramètre |b.| ||\text{Longueur du segment} = \dfrac{1}{\vert\color{#3b87cd}{b} \vert}|| -
Déterminer l'orientation des segments (point ouvert, point fermé)
Ensuite il faut déterminer de quel côté de l'extrémité fermée est notre segment. On pourra le savoir grâce au signe du paramètre |b.|
-
Si le paramètre |b| est positif alors l’extrémité fermée du segment de base se trouve à gauche du segment.
-
Si le paramètre |b| est négatif alors l’extrémité fermée du segment de base se trouve à droite du segment.
-
Trouver la distance entre les marches (contre-marches)
Le paramètre |a| permet de trouver la distance entre 2 segments. ||\vert\color{#ec0000}{a} \vert= \text{Distance entre 2 segments}|| -
Est-ce que l'escalier monte ou descend?
Pour placer un 2e segment, nous aurons besoin de savoir si la fonction est croissante ou décroissante. ||\text{Pente de l'escalier}=\color{#ec0000}{a} \color{#3b87cd}{b}||
-
Si la pente de l’escalier est positive alors la fonction est croissante.
-
Si la pente de l’escalier est négative alors la fonction est décroissante.
On veut tracer le graphique de la fonction en escalier suivante.||f(x) = \color{#ec0000}{2} \left[\color{#3b87cd}{-\dfrac{1}{4}}(x-3) \right]+4||
-
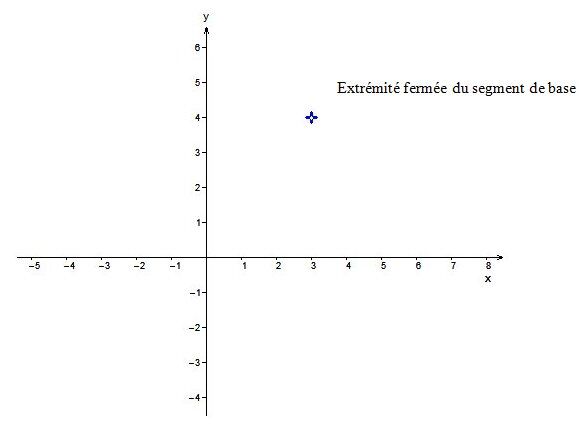
Les coordonnées de l’extrémité fermée de notre segment de base seront |(3,4).|
-
La longueur du segment (longueur de la marche) ||\begin{align} \text{Longueur du segment} &= \dfrac{1}{\vert\color{#3b87cd}{b}\vert} \\ &= \dfrac{1}{\vert \color{#3b87cd}{-0{,}25}\vert} \\ &= 4\ \text{unités} \end{align}||
-
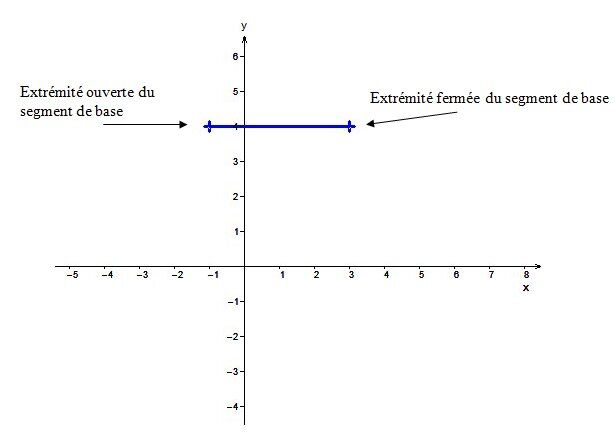
L’orientation du segment de base (sens des points)
Puisque le paramètre |b| est négatif, alors l’extrémité fermée du segment de base se trouve à droite de celui-ci.
-
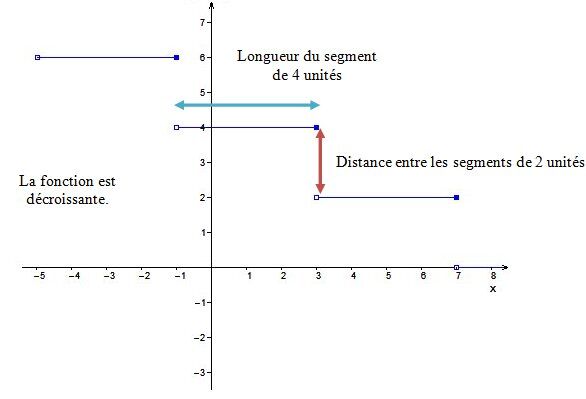
La distance entre 2 segments (contre-marche) ||\begin{align} \vert \color{#ec0000}{a} \vert &= \text{Distance entre 2 segments} \\ \vert \color{#ec0000}{2} \vert &= \text{Distance entre 2 segments} \\ \color{#ec0000}{2}\ \text{unités} &= \text{Distance entre 2 segments}\end{align}||
-
La croissance ou la décroissance de la fonction ||\begin{align} \text{Pente de l'escalier} &= \color{#ec0000}{a} \color{#3b87cd}{b} \\ &= \color{#ec0000}{(2)} \color{#3b87cd}{\left(-\dfrac{1}{4} \right)} \\&= -\dfrac{1}{2} \end{align}||Puisque la pente de notre fonction est négative alors la fonction est décroissante.
Il est donc maintenant possible de placer les autres segments de la fonction demandée.
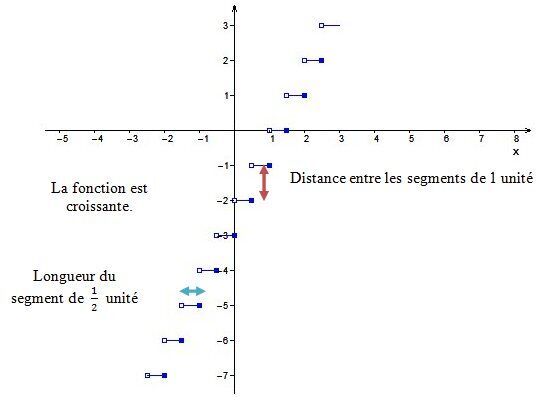
On veut tracer le graphique de la fonction en escalier suivante.||f(x)=-1[-2x-2]-5||
-
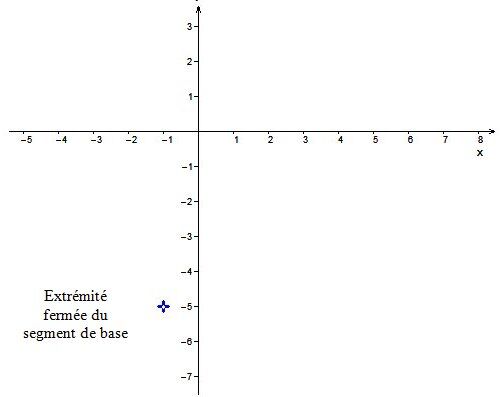
Les coordonnées de l’extrémité fermée du segment de base seront |(-1,-5).|
Pour déterminer ce point, il est nécessaire de ramener la fonction sous la forme canonique : ||f(x)=-1[-2(x+1)]-5.||
-
La longueur du segment (longueur de la marche) ||\begin{align} \text{Longueur du segment} &= \dfrac{1}{\vert\color{#3b87cd}{b}\vert} \\ &= \dfrac{1}{\vert\color{#3b87cd}{-2}\vert} \\ &= \dfrac{1}{2}\ \text{unité} \end{align}||
-
L’orientation du segment de base (sens des points)
Puisque le paramètre |b| est négatif, alors l’extrémité fermée du segment de base se trouve à droite du segment.

-
La distance entre 2 segments (contre-marche) ||\begin{align} \vert \color{#ec0000}{a}\vert &= \text{Distance entre 2 segments} \\ \vert \color{#ec0000}{-1}\vert &= \text{Distance entre 2 segments} \\ 1\ \text{unité} &= \text{Distance entre 2 segments} \end{align}||
-
La croissance ou la décroissance de la fonction. ||\begin{align} \text{Pente de l'escalier} &= \color{#ec0000}{a} \color{#3b87cd}{b} \\ &= \color{#ec0000}{(-1)} \color{#3b87cd}{(-2)} \\ &= 2 \\ \end{align}||Puisque la pente de la fonction est positive alors celle-ci est croissante.
Il est donc maintenant possible de placer les autres segments de la fonction demandée.