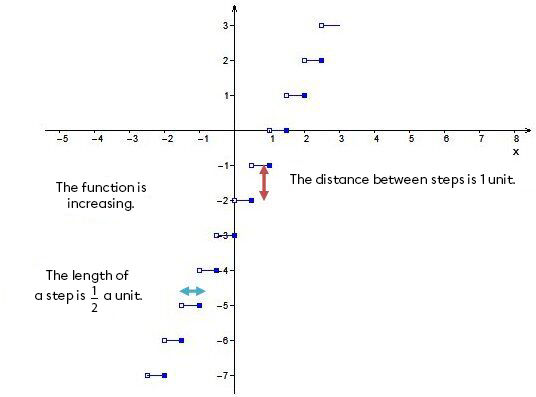
Here is how to sketch the graph of a step function (greatest integer function):
-
Find the starting point
The most important point on the graph of a greatest integer function is the closed end (solid point) of the segment, which is called the base step. -
Find the length of the steps (segments)
Once the closed end of the base step has been correctly positioned, the length of the segments must be found. The length of the segments is related to the value of the parameter |b|.
||\text{Step length} = \dfrac{1}{\mid \color{blue}{b} \mid}|| -
Determine the orientation of the steps (open point, closed point)
Next, determine which side is the closed end of the step. It depends on the sign of parameter |b|.
-
If parameter |b| is positive, then the closed end of the base segment is to the left of the step.
-
If parameter |b| is negative, then the closed end of the base segment is to the right of the step.
-
Find the distance between the steps (step height)
The parameter |a| allows us to find the vertical distance between two steps.
||\vert\color{red}{a} \vert= \text{Distance between two steps}|| -
Do the steps go upwards or downwards?
Placing a second step requires knowing if the function is increasing or decreasing.
||\text{Step slope}=\color{red}{a} \color{blue}{b}||
-
If the step’s slope is positive, the function is increasing.
-
If the step’s slope is negative, the function is decreasing.
We want to sketch the graph of the following step function:
||f(x) = \color{red}{2} \left[\color{blue}{-\frac{1}{4}}(x-3) \right]+4||
-
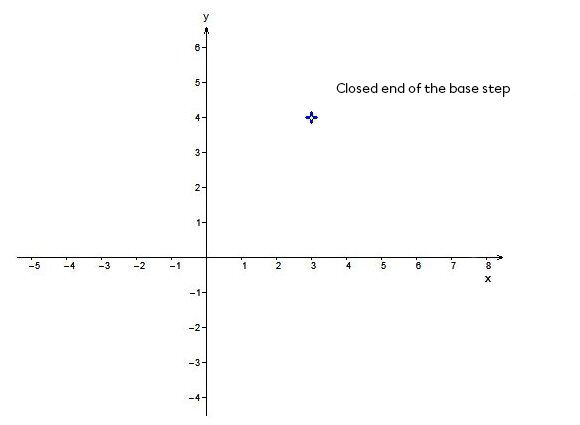
The coordinates of the closed end of our base step are |(3,4).|
-
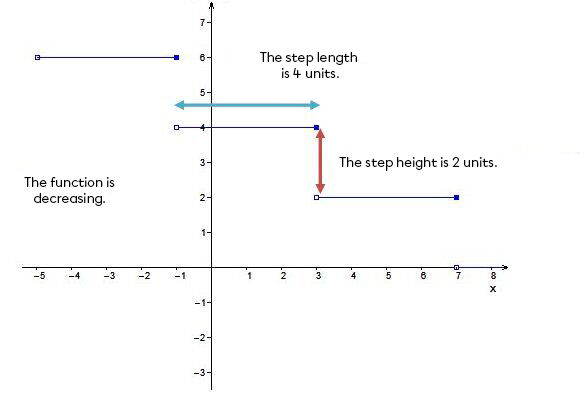
The length of the step (length of the segment) is:
||\begin{align} \text{Step length} &= \dfrac{1}{\mid \color{blue}{b}\mid} \\ \text{Step length} &= \dfrac{1}{\mid \color{blue}{-0{.}25}\mid} \\ \text{Step length} &= 4\ \text{units} \end{align}|| -
The orientation of the base step (direction of the points) is:
Since parameter |b| is negative, the closed end of the base step is to the right of it.

-
The distance between two steps (step height):
||\begin{align} \mid \color{red}{a} \mid &= \text{Distance between two steps} \\ \mid \color{red}{2} \mid &= \text{Distance between two steps} \\ \color{red}{2}\ \text{units} &= \text{Distance between two steps}\end{align}|| -
The direction of the function (whether it increases or decreases) is determined as follows: ||\begin{align} \text{Step slope} &= \color{red}{a} \color{blue}{b} \\ \text{Step slope} &= \color{red}{(2)} \color{blue}{\left(-\frac{1}{4} \right)} \\ \text{Step slope} &= -\frac{1}{2} \end{align}||
Since the slope of the function is negative, the function is decreasing.
Therefore, it is now possible to place the other steps of the function.
We want to plot the graph of the following step function: ||f(x)=-1[-2x-2]-5||
-
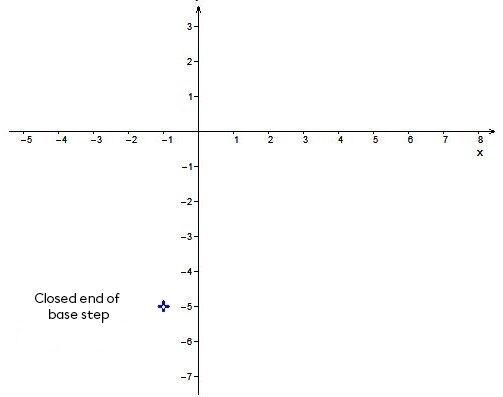
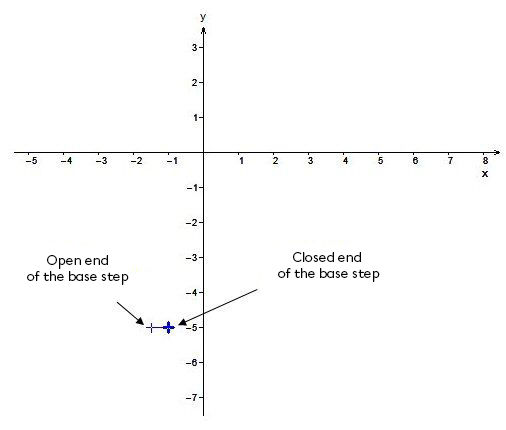
The coordinates of the closed end of the base step are |(-1,-5).| To determine the point, it is necessary to switch the function to standard form:
||f(x)=-1[-2(x+1)]-5.||
-
The length of the step (length of the segment).
||\begin{align} \text{Step length} &= \frac{1}{\mid\color{blue}{b}\mid} \\ \text{Step length} &= \frac{1}{\mid\color{blue}{-2}\mid} \\ \text{Step length} &= \frac{1}{2}\ \text{unit} \end{align}|| -
The orientation of the base step (direction of the points).
Since parameter |b| is negative, the closed end of the base step is to the right of the step.
-
The distance between two steps (segment height). ||\begin{align} \mid \color{red}{a}\mid &= \text{Distance between two steps} \\ \mid \color{red}{-1}\mid &= \text{Distance between two steps} \\ 1\ \text{unité} &= \text{Distance between two steps} \end{align}||
-
The direction of the function (whether it increases or decreases).
||\begin{align} \text{Step slope} &= \color{red}{a} \color{blue}{b} \\ \text{Step slope} &= \color{red}{(-1)} \color{blue}{(-2)} \\\text{Step slope} &= 2 \\ \end{align}||Since the slope of the function is positive, it is increasing.
So, it is now possible to place the other steps of the function.