Voici les deux méthodes pour trouver l'équation d'une fonction en escalier :
-
Pour les paramètres |(h,k)|, on prend l’extrémité fermée d'un segment (peu importe lequel, mais en pratique on prend un |(h,k)| près des axes).
-
On calcule la hauteur entre deux segments pour déterminer la valeur de |a| (en valeur absolue, c'est-à-dire sans son signe).
-
On calcule la valeur du paramètre |b| en fonction de la longueur d'un segment (en valeur absolue, c'est-à-dire sans son signe).
-
On analyse le sens des points (point ouvert, point fermé) pour donner le bon signe au paramètre |b|.
-
On regarde la croissance ou la décroissance de la fonction puis le paramètre |b| afin de déterminer le signe du paramètre |a|.
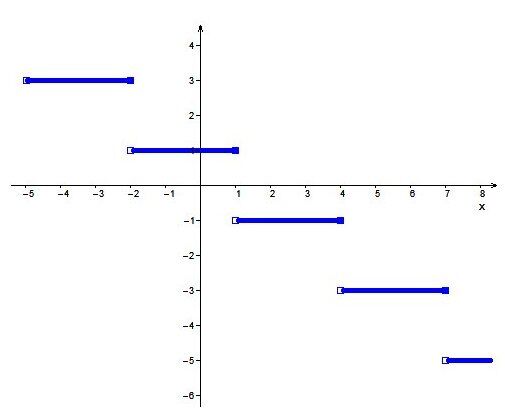
On doit trouver l'équation à partir de ce graphique :
-
Pour les paramètres |(h,k)|, on prend le segment dont l’extrémité fermée est la plus proche de l’origine.
Le point fermé le plus près des axes dans ce graphique a pour coordonnées (1,1). Donc les valeurs du couple |(h,k)| seront |h=1| et |k=1|. -
On calcule la hauteur entre deux segments pour déterminer la valeur de |a| (sans son signe).
Dans cette situation, la hauteur entre deux segments est de 2 unités, donc |a=2|. -
On calcule la valeur du paramètre |b| (sans son signe) en fonction de la largeur d'un segment.
La largeur d'un segment est de 3 unités, la valeur de |b| se calcule ainsi : ||{\mid}\color{#333fb1}b{\mid} = \dfrac{1}{\text{Longueur du segment}} =\dfrac{1}{3}|| -
On analyse le sens des points pour donner le bon signe au paramètre |b.|
Sur un segment du graphique, on observe que les points sont ouverts-fermés, donc la valeur de |b| est négative.||b=-\dfrac{1}{3}|| -
On regarde la croissance de la fonction avec les paramètres |a| et |b.|
La fonction est décroissante donc les signes de |a| et |b| doivent être contraires. Dans cet exemple, |b| est négatif donc |a| doit être positif. ||a=2||
L'équation de la fonction est donc : ||f(x)=2\left[\dfrac{-1}{3}(x-1)\right]+1||
-
Déterminer la longueur du segment de base (longueur de la marche) grâce à la longueur des intervalles en lien avec la variable |x.| Utiliser cette valeur pour trouver la valeur du paramètre |b| (sans son signe).
-
Trouver la valeur du paramètre |a| (sans son signe) en calculant la différence entre deux valeurs de |y| dont les deux intervalles correspondant sont consécutifs.
-
Trouver le signe du paramètre |b| selon le sens des crochets |[| des intervalles.
-
Trouver le signe du paramètre |a| selon la croissance ou la décroissante de la fonction et le signe du paramètre |b|.
-
Trouver un couple |(h,k)| correspondant à une extrémité fermée d'un intervalle.
Trouvez l'équation de la fonction en escalier dont la table de valeur est :
| |x| | |y| |
|---|---|
| |[-4,-2[| | |5| |
| |[-2,0[| | |6| |
| |[0,2[| | |7| |
| |[2,4[| | |8| |
-
La longueur des intervalles est de 2 ce qui correspond à la longueur du segment de base. Il faut trouver la valeur du paramètre |b| : ||\begin{align} \text{Longueur du segment de base } &= \dfrac{1}{{\mid}b{\mid}} \\ 2 &= \dfrac{1}{{\mid}b{\mid}} \\ \Rightarrow\ {\mid}b{\mid} &= \dfrac{1}{2} \end{align}||
-
La valeur du paramètre |a| correspond au saut effectué d'un segment à l'autre (la variation de |y|).
Ici, |{\mid}a{\mid} = 1.| -
Les crochets étant |[ , [| ceci indique que le sens des points est fermé-ouvert. Ainsi, le paramètre |b| sera positif et vaudra donc |b = \dfrac{1}{2}.|
-
Lorsque les valeurs de |x| augmentent, les valeurs de |y| augmentent également. Donc, la fonction est croissante |(a \times b >0)| et ainsi comme |b| est positif cela force |a| à l'être également. Par conséquent, |a=1.|
-
Comme couple |(h,k).| on peut prendre |(0,7).|
Ainsi, l'équation de la fonction en escalier donnée par la table de valeurs ci-dessus est : ||f(x) = 1 \left[\dfrac{1}{2}(x) \right] + 7||
Dans un problème écrit, il est fortement suggéré de tracer le graphique ou de bâtir une table de valeurs pour trouver l'équation d'une fonction en escalier.