There are two methods for finding the rule of a step function.
-
For the parameters |(h,k)|, use the closed end of a segment (it doesn't matter which one, but it is common to use a point |(h,k)| near the axes).
-
Calculate the height difference between two segments to determine the (absolute) value of |a| (i.e. without its sign).
-
Calculate the (absolute) value of the parameter |b| (i.e. without its sign) using the length of a step.
-
Analyze the direction of the points (open point, closed point) to give the correct sign to the parameter |b|.
-
Analyze if the function is increasing or decreasing and use the parameter |b| to determine the sign of the parameter |a|.
Find the rule of the function in the following graph.
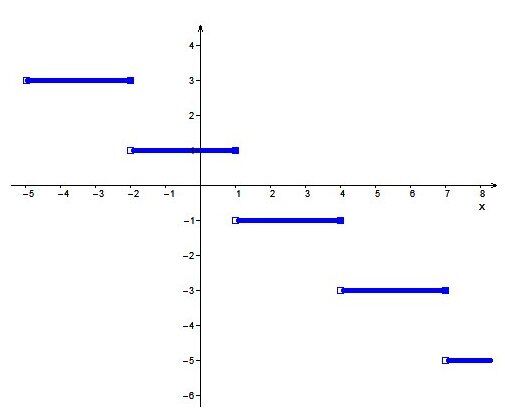
-
For parameters |(h,k)|, use the step with a closed end closest to the origin
The closed point that is closest to the axes in this graph has coordinates |(1,1)|. So the value of the coordinate |(h,k)| will be |h=1| and |k=1|. -
Calculate the height difference between two segments to determine the value of |a| (without its sign)
In this situation, the difference of height between two segments is |2| units, so |a=2.| -
Calculate the value of the parameter |b| (without its sign) using the width of a segment
The width of a segment is |3| units, so the value of |b| is calculated as follows. ||{\mid}\color{#333fb1}b{\mid} = \dfrac{1}{\text{Length of a segment}} =\dfrac{1}{3}|| -
Analyze the direction of the points to assign the right sign to the parameter |b|
On a segment of the graph, observe that the points are open on the left, closed on the right, so the value of |b| is negative.||b=-\dfrac{1}{3}|| -
Notice the increasing or decreasing intervals in the function and the parameters |a| and |b|
Notice the increasing or decreasing intervals in the function and the parameters |a| and |b.| The function is decreasing, so the signs of |a| and |b| must be opposite. In this example, |b| is negative so |a| must be positive. ||a=2||
Therefore, the function’s rule is the following. ||f(x)=2\left[\dfrac{-1}{3}(x-1)\right]+1||
-
Determine the length of a segment (length of a step) using the magnitude of the |x| intervals. Use this value to find the value of the parameter |b| (without its sign).
-
Find the value of the parameter |a| (without its sign) by calculating the difference between two values of |y| corresponding to consecutive intervals.
-
Find the sign of the parameter |b| according to the brackets |[| in the intervals.
-
Find the sign of the parameter |a| by determining whether the function increases or decreases and using the sign of the parameter |b|.
-
Find the values of some coordinate pair |(h,k)| corresponding to a closed end of an interval.
Find the rule of the step function whose table of values is the following.
|
|x| |
|y| |
|---|---|
|
|[-4,-2[| |
|5| |
|
|[-2,0[| |
|6| |
|
|[0,2[| |
|7| |
|
|[2,4[| |
|8| |
-
The length of the intervals is |2|, which corresponds to the length of a step. Find the value of the parameter |b|. ||\begin{align} \text{Length of a step} &= \dfrac{1}{{\mid}b{\mid}} \\ 2 &= \dfrac{1}{{\mid}b{\mid}} \\ \Rightarrow\ {\mid}b{\mid} &= \dfrac{1}{2} \end{align}||
-
The value of the parameter |a| corresponds to the jump made from one segment to another (the difference of |y|).
Here, |{\mid}a{\mid} = 1.| -
The brackets are: |[\ ,\,[,| indicating that the direction of the points is closed-open. Therefore, the parameter |b| will be positive and its value is |b = \dfrac{1}{2}.|
-
When the values of |x| increase, the values of |y| also increase. So the function is increasing |(a \times b >0)|, and since |b| is positive, |a| must be as well. Therefore, |a=1.|
-
For a coordinate pair |(h,k),| use |(0,7).|
So, the rule of the step function equation given by the table of values above is the following. ||f(x) = 1 \left[\dfrac{1}{2}(x) \right] + 7||
With a word problem, it is strongly suggested to draw a graph or build a table of values to find the rule of a step function.