L'addition de vecteurs par la méthode des composantes permet de trouver le vecteur résultant de la combinaison mathématique de deux ou plusieurs vecteurs.
Lorsqu'un plan cartésien est dessiné à l'échelle, on peut reporter les vecteurs sur les axes pour en déterminer les composantes. Il suffit ensuite de les additionner pour trouver la grandeur et l'orientation du vecteur résultant.
Quelle est la somme des vecteurs représentés ci-dessous ?
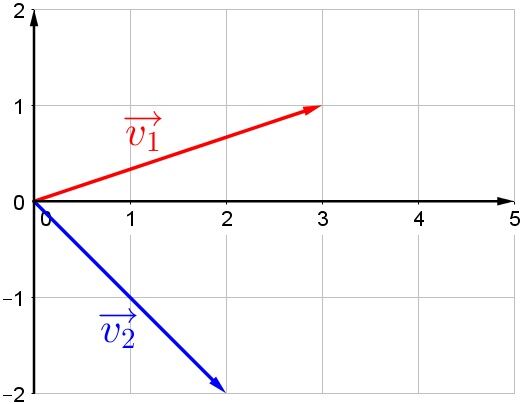
Il est possible de déterminer chacune des composantes des vecteurs suivants en les reportant sur les axes des abscisses et des ordonnées.
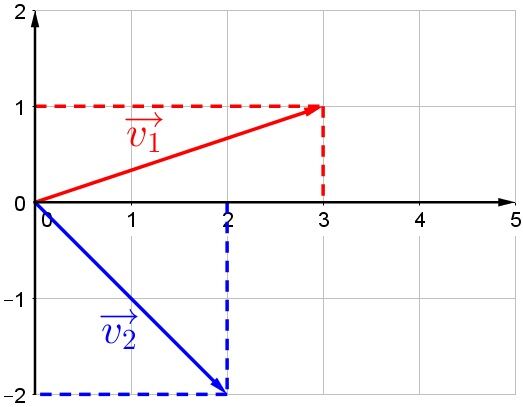
| | Composante horizontale | Composante verticale |
| Vecteur rouge | |\color{red} {3}| | |\color{red} {1}| |
| Vecteur bleu | |\color{blue} {2}| | |\color{blue} {-2}| |
| Somme des composantes | |\color{red} {3} + \color{blue} {2} = 5| | |\color{red} {1} + \color{blue} {-2} = -1| |
Le vecteur résultant peut être représenté dans le plan cartésien (vecteur noir).
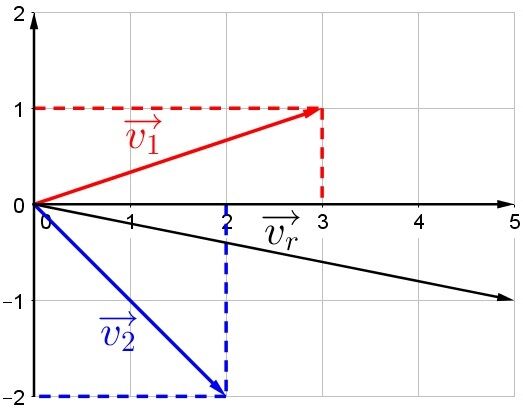
On peut ensuite trouver la grandeur et l'orientation de ce vecteur.
||\begin{align} r = \sqrt{x^2 + y^2} \quad \Rightarrow \quad r &= \sqrt{ {5^2} + {(-1)^2}} \\ &= \sqrt{26}\\ & \approx 5,1 \: \text{u} \end{align}||
||\begin{align} \theta=\tan^{-1} \left( \displaystyle \frac{ {y}}{ {x}} \right)\quad \Rightarrow \quad \theta &=\tan^{-1} \displaystyle \left( \frac{ {-1}}{{5}} \right)\\
&= \tan^{-1}\left(-0,2 \right)\\
& \approx -11,3^{\circ}\end{align}||
L'angle déterminé représente l'angle représenté en orange dans l'image ci-dessous. Toutefois, il faut toujours trouver l'angle par rapport à l'axe des abscisses positif, soit l'angle représenté en vert sur la même image. Ainsi, pour trouver l'angle résultant:
|360^{\circ} - \color \orange {11,3^{\circ}} = \color \green {348,7 ^ {\circ}}|
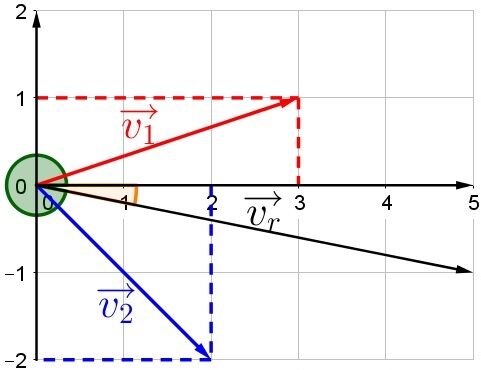
Le vecteur résultant a donc une grandeur de |\text {5,1 u}| et il est orienté à |348,7^{\circ}|.
Si on connaît uniquement les vecteurs sans avoir de graphique, il est possible de déterminer mathématiquement la valeur du vecteur résultant.
- Décomposer les vecteurs en composantes horizontales et verticales en utilisant les règles suivantes.
|x=V \cos \theta|
|y=V \sin \theta| - Additionner ensemble les composantes horizontales de tous les vecteurs. Faire de même avec les composantes verticales.
- Trouver la grandeur du vecteur résultant en utilisant la relation de Pythagore.
| r = \sqrt{x^2 + y^2}|
- Trouver l'orientation du vecteur résultant en utilisant la trigonométrie. Il faut toujours utiliser l'axe positif des abscisses comme origine pour l'angle.
| \theta=\tan^{-1}\left(\begin{array}{c}\displaystyle \frac{y}{x} \end{array}\right)|
|\overrightarrow {V_1} = \text {30 m à 60}^{\circ}|
|\overrightarrow {V_2} = \text {150 m à 210}^{\circ}|
|\overrightarrow {V_3} = \text {90 m à 270}^{\circ}|
En premier lieu, il faut décomposer les vecteurs en composantes.
| | Composante horizontale | Composante verticale |
| |\overrightarrow { V_1}| | |30 \cos 60^{\circ} = 15 \:\text {m}| | |30 \sin 60^{\circ} = 26 \: \text {m}| |
| |\overrightarrow {V_2}| | |150 \cos 210^{\circ} = -130 \: \text {m}| | |150 \sin 210^{\circ} = -75,0 \: \text {m}| |
| |\overrightarrow {V_3}| | |90 \cos 270^{\circ} = 0 \: \text {m}| | |90 \sin 270^{\circ} = -90 \: \text {m}| |
Lorsque les trois vecteurs ont été décomposés, il faut additionner les composantes horizontales de chacun des vecteurs ensemble, et faire de même avec les composantes verticales.
| | Composante horizontale | Composante verticale |
| |\overrightarrow {V_1}| | |15 \: \text {m}| | |26 \: \text {m}| |
| |\overrightarrow {V_2}| | |-130 \: \text {m}| | |-75,0 \: \text {m}| |
| |\overrightarrow {V_3}| | |0 \: \text {m}| | |-90 \: \text {m}| |
| |\text {Somme}| | |15 + -130 + 0 = - 115 \: \text {m}| | |26 + -75,0 + -90 = -139 \: \text {m}| |
Lorsque les deux composantes ont été déterminées, il est possible de calculer la grandeur du vecteur résultant.
||\begin{align} r = \sqrt{x^2 + y^2} \quad \Rightarrow \quad r &= \sqrt{ {(-115)^2} + {(-139)^2}} \\ &= \sqrt{32\:546}\\ & \approx 180 \: \text{m} \end{align}||
Pour trouver l'angle, on utilise des rapports trigonométriques, comme la tangente.
||\begin{align} \theta=\tan^{-1} \left( \displaystyle \frac{ {y}}{ {x}} \right)\quad \Rightarrow \quad \theta &=\tan^{-1} = \displaystyle \left( \frac{ {-139}}{{-115}} \right)\\
&= \tan^{-1}\left(1.208....\right)\\
& \approx 50,4^{\circ}\end{align}||
Afin de savoir ce que cet angle représente, il est important de représenter le vecteur dans un système de référence. Puisque les deux composantes sont négatives, le vecteur résultant sera situé dans le troisième quadrant.
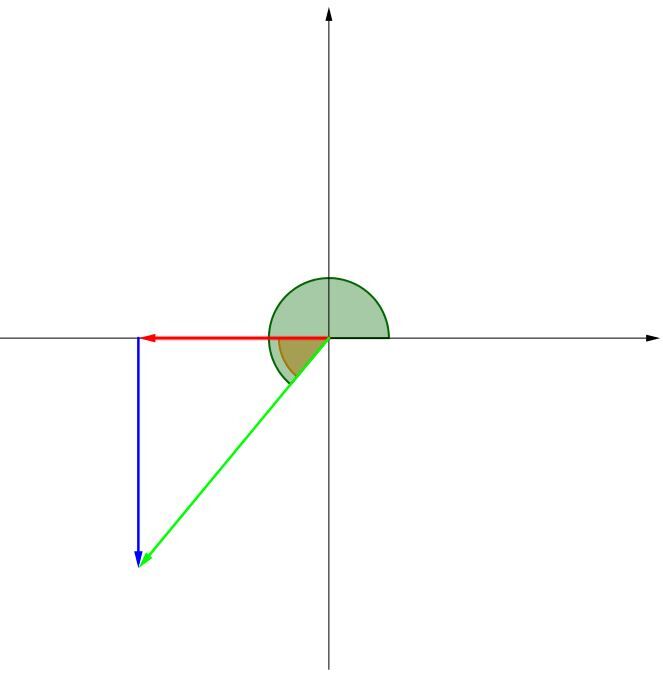
L'angle calculé est donc l'angle situé à l'intérieur du triangle formé par la composante horizontale (en rouge), la composante verticale (en bleu) et le vecteur résultant (en vert). Puisqu'il faut calculer l'angle à partir de l'axe positif des abscisses, soit l'angle représenté en vert sur le schéma, il faut donc additionner l'angle calculé (représenté en orange) sur le schéma à |\small 180^{\circ}| pour trouver l'orientation du vecteur résultant.
|180^{\circ} + 50,4^{\circ} = 230,4^{\circ}|
Le vecteur résultant a donc une grandeur de |180 \: \text {m}| et une orientation de |230,4^{\circ}|.