Vector addition using the component method makes it possible to find the vector resulting from the mathematical combination of two or more vectors.
When a Cartesian plane is drawn to scale, vectors can be plotted on the axes to determine their components. They can then be simply added together to find the magnitude and the orientation of the resultant vector.
What is the sum of the vectors shown below?
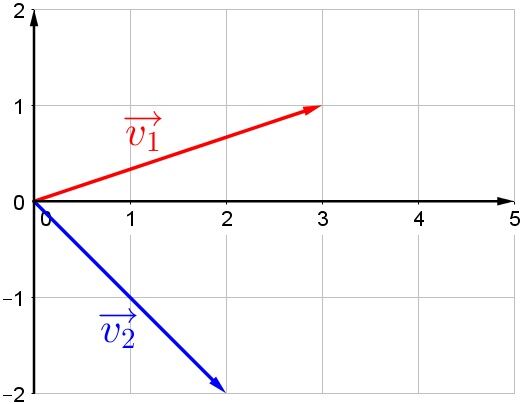
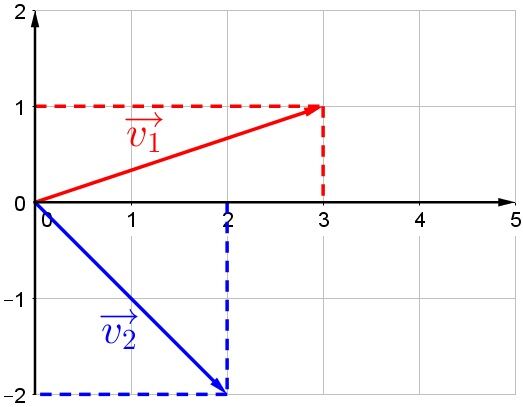
It is possible to determine each of the components of the following vectors by plotting them on the |x|-axis and |y|-axis.
| |
Horizontal component |
Vertical component |
|
Red vector |
|\color{red} {3}| |
|\color{red} {1}| |
|
Blue vector |
|\color{blue} {2}| |
|\color{blue} {-2}| |
|
Sum of components |
|\color{red} {3} + \color{blue} {2} = 5| |
|\color{red} {1} + \color{blue} {-2} = -1| |
The resultant vector can be represented in the Cartesian plane (black vector).
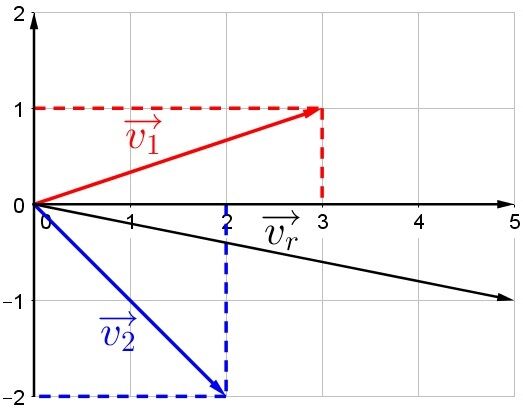
We can then find the magnitude and orientation of this vector.
||\begin{align} r = \sqrt{x^2 + y^2} \quad \Rightarrow \quad r &= \sqrt{ {5^2} + {(-1)^2}} \\ &= \sqrt{26}\\ & \approx 5.1 \: \text{u} \end{align}||
||\begin{align} \theta=\tan^{-1} \left( \displaystyle \frac{ {y}}{ {x}} \right)\quad \Rightarrow \quad \theta &=\tan^{-1} \displaystyle \left( \frac{ {-1}}{{5}} \right)\\
&= \tan^{-1}\left(-0.2 \right)\\
& \approx -11.3^{\circ}\end{align}||
The determined angle is the angle shown in orange in the image below. However, it is always necessary to find the angle relative to the positive |x|-axis, that is the angle in green on the same image. Thus, to find the resulting angle, we do the following calulations.
||360^{\circ} - \color \orange {11.3^{\circ}} = \color \green {348.7 ^ {\circ}}||
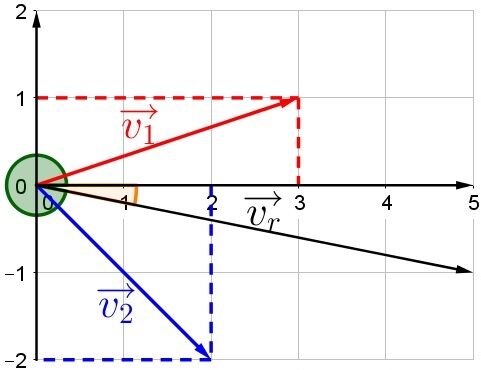
The resultant vector therefore has a magnitude of |5.1\ \text {u}| and it is oriented to |348.7^\circ.|
If the vectors are given but not graphically, it is possible to determine the value of the resultant vector mathematically.
-
Break down the vectors into horizontal and vertical components using the following rules.
||x=V \cos \theta||
||y=V \sin \theta|| -
Add together the horizontal components of all vectors. Do the same with the vertical components.
-
Find the magnitude of the resultant vector using the Pythagorean theorem.
|| r = \sqrt{x^2 + y^2}||
-
Find the orientation of the resultant vector using trigonometry. Always use the positive |x|-axis as the origin for the angle.
||\theta=\tan^{-1}\left(\begin{array}{c} \dfrac{y}{x} \end{array}\right)||
What is the result of adding the following three vectors?
|\overrightarrow {V_1} = 30 \text {m at] 60^\circ|
|\overrightarrow {V_2} = 150 \text {m at} 210^\circ|
|\overrightarrow {V_3} = 90 \text {m at} 270^\circ|
First, the vectors must be broken down into components.
|
Horizontal component |
Vertical component |
|
|
|\overrightarrow { V_1}| |
|30 \cos 60^{\circ} = 15 \:\text {m}| |
|30 \sin 60^{\circ} = 26 \: \text {m}| |
|
|\overrightarrow {V_2}| |
|150 \cos 210^{\circ} = -130 \: \text {m}| |
|150 \sin 210^{\circ} = -75.0 \: \text {m}| |
|
|\overrightarrow {V_3}| |
|90 \cos 270^{\circ} = 0 \: \text {m}| |
|90 \sin 270^{\circ} = -90 \: \text {m}| |
When the three vectors have been broken down, add the horizontal components of each vector together, and do the same with the vertical components.
|
Horizontal component |
Vertical component |
|
|
|\overrightarrow {V_1}| |
|15 \: \text {m}| |
|26 \: \text {m}| |
|
|\overrightarrow {V_2}| |
|-130 \: \text {m}| |
|-75.0 \: \text {m}| |
|
|\overrightarrow {V_3}| |
|0 \: \text {m}| |
|-90 \: \text {m}| |
|
|\text {Sum}| |
|15 + -130 + 0 = - 115 \: \text {m}| |
|26 + -75.0 + -90 = -139 \: \text {m}| |
When the two components have been determined, it is possible to calculate the magnitude of the resultant vector.
||\begin{align} r = \sqrt{x^2 + y^2} \quad \Rightarrow \quad r &= \sqrt{ {(-115)^2} + {(-139)^2}} \\ &= \sqrt{32\:546}\\ & \approx 180 \: \text{m} \end{align}||
To find the angle, use trigonometric ratios, like the tangent.||\begin{align} \theta=\tan^{-1} \left( \dfrac{ {y}}{ {x}} \right)\quad \Rightarrow \quad \theta &=\tan^{-1} = \left( \dfrac{ {-139}}{{-115}} \right)\\
&= \tan^{-1}\left(1.208....\right)\\
& \approx 50.4^\circ\end{align}||
In order to know what this angle represents, it is important to represent the vector in a reference system. Since both components are negative, the resultant vector will be located in the third quadrant.
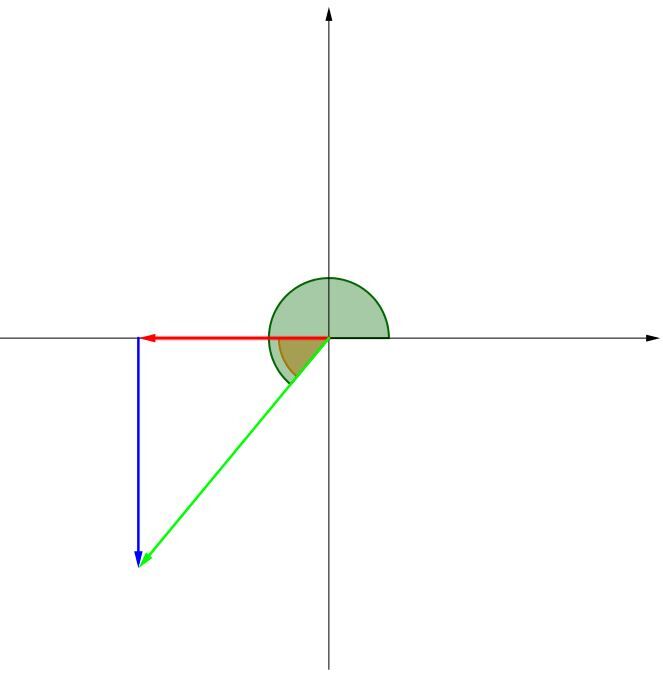
The calculated angle is therefore the angle located inside the triangle formed by the horizontal component (in red), the vertical component (in blue), and the resultant vector (in green). Since the angle must be calculated from the positive |x|-axis, that is, the angle shown in green on the diagram, the calculated angle (shown in orange) in the diagram must be added to |180^\circ| to find the orientation of the resultant vector.
||180^\circ + 50.4^\circ = 230.4^\circ||
The resultant vector therefore has a magnitude of |180 \: \text {m}| and an orientation of |230.4^\circ.|