Pour déterminer ce qu'est le déplacement et la distance parcourue, il faut d'abord déterminer le mouvement qu'a fait un mobile, c'est-à-dire sa trajectoire.
La trajectoire d’un objet en mouvement correspond à l’ensemble des positions qu’a occupées cet objet tout au long de son mouvement.
Concrètement, la trajectoire peut aussi être définie comme une ligne qui décrit le mouvement de l’objet.
Sur le schéma ci-dessous, on observe la trajectoire d’un papillon grâce à une ligne pointillée.

La distance parcourue est la mesure de l’ensemble des positions qu’a occupées cet objet tout au long de son mouvement.
Dans une voiture, l’odomètre mesure la distance parcourue. Son action se poursuit, peu importe quel mouvement la voiture effectue, que ce soit de tourner à une intersection ou de se déplacer à reculons.
Sur l’illustration de la trajectoire du papillon, la distance parcourue doit être déterminée en mesurant la longueur de la ligne pointillée. Pour ce faire, on peut s’imaginer que la ligne pointillée est une corde. Ainsi, pour obtenir la distance parcourue, il faudrait étirer la corde pour en faire une ligne droite et en mesurer la longueur.
Dans un mouvement composé de plusieurs mouvements distincts, on détermine la distance parcourue en faisant la somme des longueurs de chacun de ces mouvements.
La distance parcourue, définie par la variable |d|, est calculée par la formule:
|d= \mid \triangle x_{1}\mid+\mid\triangle x_{2}\mid+ \mid\triangle x_{3}\mid+...|
où
|d| représente la distance parcourue |\small \text {(m)}|
|\triangle x| représente les mouvements effectués par le mobile, en valeur absolue (valeur positive) |\small \text {(m)}|
La distance parcourue n'est pas une mesure orientable. Il est impossible de savoir vers où un mobile se déplace en utilisant la distance parcourue, car cette mesure se calcule, peu importe le mouvement effectué. On dit que la distance parcourue est une mesure scalaire, soit un nombre suivi d'une unité de mesure sans tenir compte de l'orientation.
Le déplacement représente la distance orientée qui sépare le point de départ du point d’arrivée.
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p>Il s’agit en fait d’un <a href="/fr/eleves/bv/mathematiques/les-vecteurs-m1298">vecteur</a>, puisque le déplacement possède à la fois une grandeur, une direction et un sens. On le représente par une flèche ayant pour origine le point de départ du déplacement et se terminant au point d'arrivée. C'est l'équivalent d'un vol d'oiseau entre deux points.</p>
</body></html>
Dans l'exemple du papillon illustré plus tôt, on peut déterminer le déplacement du papillon en dessinant une flèche entre le point de départ et le point d'arrivée.
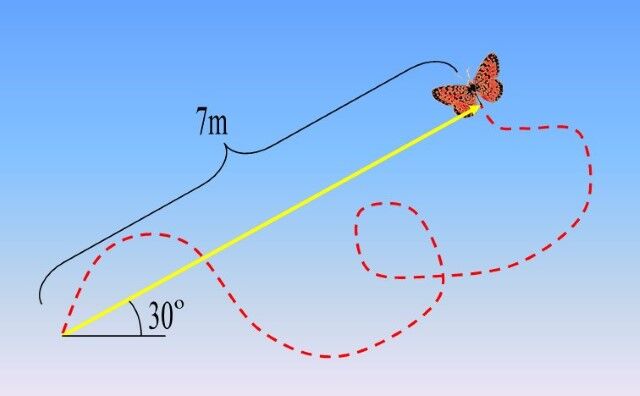
Le papillon a donc fait un déplacement de |\text {7 m à 30}^{\circ}| par rapport à l'horizontale. Rappelons que le déplacement doit toujours être orienté par rapport à l'axe polaire, soit l'axe des abscisses positif.
Le déplacement, défini par la variable |\triangle x|, est calculé par la formule:
|\triangle x=x_{f}-x_{i}|
où
|\triangle x| représente le déplacement |\small \text {(m)}|
|x_{f}| représente la position finale du mobile |\small \text {(m)}|
|x_{i}| représente la position initiale du mobile |\small \text {(m)}|
Il est donc important de savoir précisément ce qu'on cherche dans un problème, puisque la mesure de la distance parcourue n'est pas toujours la même que celle du déplacement.
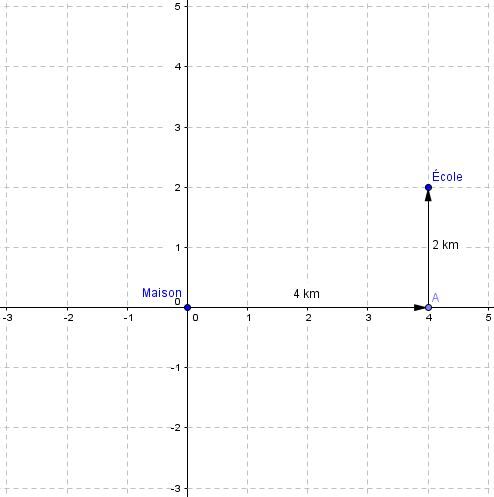
Un élève quitte sa maison à pied pour se rendre à l'école. Il marche selon la trajectoire illustrée ci-dessous. Quelle est la distance parcourue et quel est le déplacement effectué par l'élève?
Distance parcourue
Pour déterminer la distance parcourue, il faut calculer la longueur entre la maison et l'école. Puisqu'il parcourt |\small \text {4 km}| vers l'est et |\small \text {2 km}| vers le nord, on peut donc calculer la distance parcourue en faisant la somme des deux mouvements.
||\begin{align}
d= \mid \triangle x_{1}\mid+\mid\triangle x_{2}\mid
\quad \Rightarrow \quad
d&= \mid \text {4 km}\mid+\mid\text{2 km}\mid \\
&= \text {6 km}
\end{align}||
Déplacement
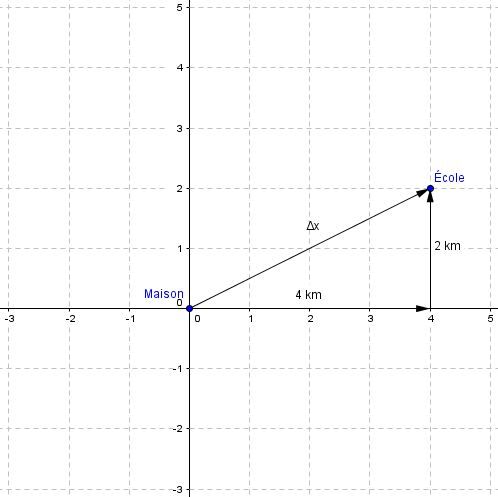
Pour déterminer le déplacement, il faut représenter le vecteur entre le point de départ et le point d'arrivée.
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p>Il faut utiliser la relation de Pythagore pour déterminer la distance entre le point de départ et le point d'arrivée. Par la suite, pour calculer l'orientation du vecteur, les relations trigonométriques permettront de déterminer l'angle entre l'axe polaire et le vecteur. Il faut suivre la même démarche que celle utilisée lorsqu'on cherche les <a href="/fr/eleves/bv/physique/le-systeme-de-reference-p1001#les-coordonnees-polaires"> coordonnées polaires</a> dans une mise en situation donnée.<br>
||\begin{align} r = \sqrt{x^2 + y^2} \quad \Rightarrow \quad r &= \sqrt{ {4^2} + {2^2}} \\ &= \sqrt{20}\\ & \approx 4,47 \: \text{km} \end{align}||<br>
||\begin{align} \theta=\tan^{-1} \left( \displaystyle \frac{ {y}}{ {x}} \right)\quad \Rightarrow \quad \theta &=\tan^{-1} = \displaystyle \left( \frac{ {2}}{{4}} \right)\\ &= \tan^{-1}\left(0,5\right)\\ & \approx 26,6^{\circ}\end{align}||<br>
<br>
Le déplacement fait par l'élève de sa maison jusqu'à l'école est de |\text {4,47 km}| à |26,6^{\circ}|.</p>
<p> </p>
</body></html>
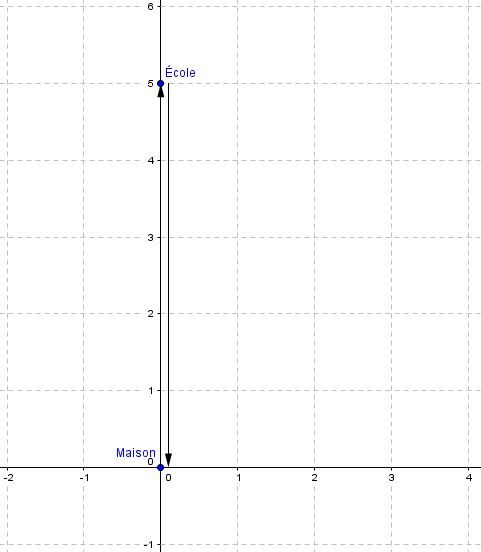
Une autre élève quitte sa maison pour se rendre à l'école. Toutefois, rendue à l'école, elle s'aperçoit qu'il n'avait pas d'école, car c'est une journée de congé. Elle retourne donc chez elle. Quelle est la distance parcourue et quel est le déplacement de cette élève?
Distance parcourue
Pour déterminer la distance parcourue, il faut tenir compte qu'elle a tout d'abord fait le chemin entre la maison et l'école, puis elle a refait le même chemin pour retourner chez elle. On peut donc calculer la distance parcourue en faisant la somme des deux mouvements.
||\begin{align}
d= \mid \triangle x_{1}\mid+\mid\triangle x_{2}\mid
\quad \Rightarrow \quad
d&= \mid \text {5 km}\mid+\mid\text{5 km}\mid \\
&= \text {10 km}
\end{align}||
Déplacement
Pour déterminer le déplacement, il faut représenter le vecteur entre le point de départ et le point d'arrivée. Toutefois, ces deux points sont identiques: son point de départ est sa maison, tout comme son point d'arrivée. Il n'y a donc aucun déplacement, car il n'y a aucune différence entre le point de départ et le point d'arrivée. Dans cette situation, |\triangle x = \text {0 km}|.
Il est possible, dans certaines situations, que le déplacement soit nul. Toutefois, à moins que l'objet ne soit immobile, sa distance parcourue sera toujours supérieure à 0.
Dans l'exemple ci-dessus, la variable |\triangle x| a été utilisée pour calculer les coordonnées polaires. Il est important de noter que cette variable est semblable à la variable |r| utilisée dans les exemples avec les coordonnées polaires.