To determine what is displacement and distance covered, we first need to identify the kind of motion an object is doing, i.e. its trajectory.
The trajectory of a moving object is the set of positions occupied by that object throughout its movement.
In practical terms, the trajectory can also be defined as a line that describes the object's movement.
The diagram below shows a dotted line corresponding to a butterfly's trajectory.

The distance covered is the length of the trajectory followed by an object, regardless of its orientation.
In a car, the odometer measures the distance covered. It continues to add up the distance, whether turning at a junction or driving backward.
In the illustration of the butterfly's trajectory, the distance covered must be determined by measuring the length of the dotted line. We can imagine that the dotted line is a string to do this. You would have to stretch the string to make a straight line and measure its length to obtain the distance covered.
In a movement made up of several distinct movements, the distance covered is the sum of the lengths of each of these movements.
As defined by the variable |d|, the distance covered is calculated with the formula:
|d= \mid \triangle x_{1}\mid+\mid\triangle x_{2}\mid+ \mid\triangle x_{3}\mid+...|
where
|d| represents the distance covered |\small \text {(m)}|
|\triangle x| represents the movements made by the vehicle, in absolute value (positive value) |\small \text {(m)}|
Distance covered is a measure that has no orientation. Since this measurement is made regardless of the movement's orientation, it is impossible to know where a moving object is going by using the distance covered. We say that distance covered is a scalar measurement, i.e. a number followed by a unit of measurement that takes no account of orientation.
Displacement represents the oriented straight line distance separating the points of departure and arrival.
In the butterfly example illustrated earlier, its displacement can be visualized by drawing an arrow between the starting and arriving points.
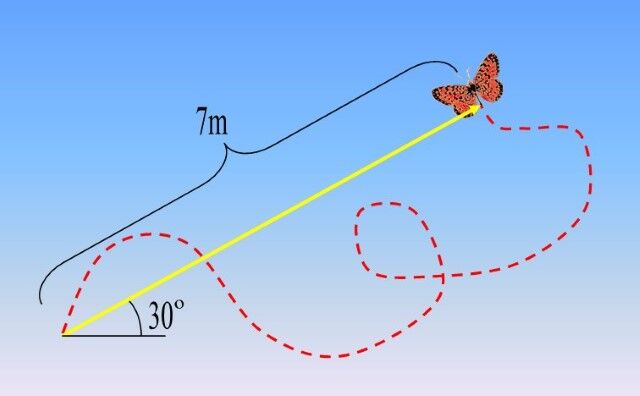
The butterfly therefore made a displacement of |\text {7 m at 30}^{\circ}| above the horizon. Remember that the displacement must always be expressed according to the polar axis, i.e. the positive x-axis.
As defined by the variable |\triangle x|, displacement is calculated by the formula:
|\triangle x=x_{f}-x_{i}|
where
|\triangle x| represents the displacement |\small \text {(m)}|
|x_{f}| represents the final position of the vehicle |\small \text {(m)}|
|x_{i}| represents the initial position of the vehicle |\small \text {(m)}|
In a given problem, it is important to know what you are asking to find since the value of the distance covered is not always the same as that of displacement.
A pupil is walking from home to school. He walks along the path illustrated below. What are the distance covered and the displacement made by the pupil?
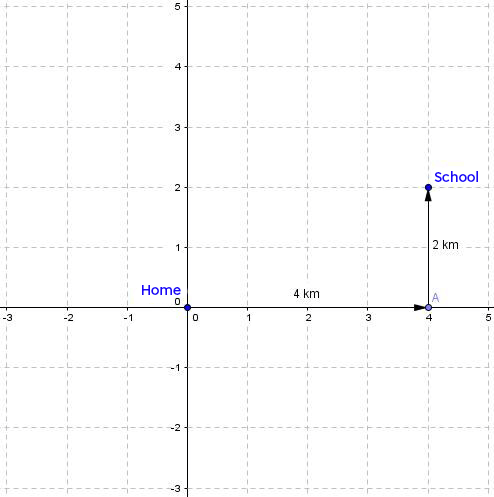
Distance covered
To find the distance covered, we have to calculate the path length between home and school. Since he travels |\small \text {4 km}| eastward and |\small \text {2 km}| northward, we can calculate the distance covered by summing both movements.
||\begin{align}
d= \mid \triangle x_{1}\mid+\mid\triangle x_{2}\mid
\quad \Rightarrow \quad
d&= \mid \text {4 km}\mid+\mid\text{2 km}\mid \\
&= \text {6 km}
\end{align}||
Displacement
To determine the displacement, we will draw the vector between the points of departure and arrival.
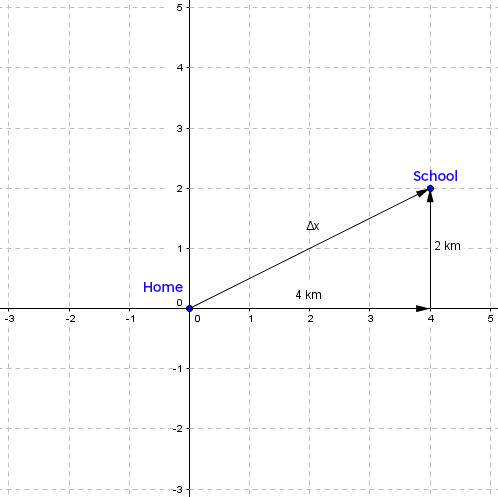
To calculate the distance between the starting and arriving points, we have to use the Pythagorean relationship. Afterward, trigonometric relations are used to calculate the orientation of the vector, i.e. the angle between the polar axis and the vector. Proceed in the same way as for finding the polar coordinates in a given situation.
||\begin{align} r = \sqrt{x^2 + y^2} \quad \Rightarrow \quad r &= \sqrt{ {4^2} + {2^2}} \\ &= \sqrt{20}\\ & \approx 4,47 \: \text{km} \end{align}||
||\begin{align} \theta=\tan^{-1} \left( \displaystyle \frac{ {y}}{ {x}} \right)\quad \Rightarrow \quad \theta &=\tan^{-1} = \displaystyle \left( \frac{ {2}}{{4}} \right)\\ &= \tan^{-1}\left(0,5\right)\\ & \approx 26,6^{\circ}\end{align}||
From home to school, the displacement of the pupil is |\text {4,47 km}| at |26,6^{\circ}|.
A second pupil left home for school. However, once she got there, she realized there was no class because it was a school holiday. So she got back home. What is the distance covered and the displacement made by this pupil?

Distance covered
To determine the distance covered, you must consider that she first walked between home and school and then back home. So we can calculate the distance covered by adding up the two movements.
||\begin{align}
d= \mid \triangle x_{1}\mid+\mid\triangle x_{2}\mid
\quad \Rightarrow \quad
d&= \mid \text {5 km}\mid+\mid\text{5 km}\mid \\
&= \text {10 km}
\end{align}||
Displacement
To calculate the displacement, we need to trace the vector between the points of departure and arrival. However, these two points are the same: her point of departure and her point of arrival are both at the same location, i.e. her home. Since there is no gap between the starting and the ending points, there is no displacement. In this situation, |\triangle x = \text {0 km}|.
As you can see, in some situations the displacement may be zero. However, unless the object is stationary, its distance covered will always be greater than 0.
In the above example, the variable |\triangle x| was used to calculate the polar coordinates. It's important to note that this variable is similar to the |r| variable used in the examples with polar coordinates.