La chambre noire, ou camera obscura en latin, est un instrument optique servant à recueillir une image sur une surface plane.
Un sténopé est un petit trou étroit par lequel la lumière peut entrer pour aller dans une chambre noire.
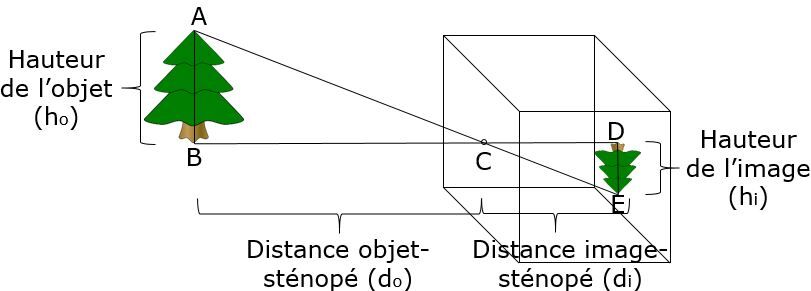
La chambre noire est constituée d'un contenant fermé et opaque sur lequel on perce un petit trou (le sténopé) à travers lequel la lumière pourra entrer pour former une image. Le sténopé utilise le principe optique selon lequel la lumière voyage en ligne droite. Le schéma suivant démontre le fonctionnement du sténopé.
Dans l'image ci-dessus, les rayons provenant de la cime de l’arbre (haut de l’arbre) se retrouvent en bas et vice-versa. L'image produite à l'intérieur d'un sténopé sera donc toujours inversée. De plus, tous les rayons provenant de l’objet se croiseront dans le sténopé.
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p>L'utilisation d'une chambre noire peut également permettre de calculer la hauteur d’un immeuble ou encore une distance nous séparant d’un objet à l’aide de simples calculs mathématiques.</p>
<p>Comme les triangles ABC et CDE sont tous les deux de triangles rectangles et qu’ils sont opposés par les sommets, ce sont nécessairement des <a href="/fr/eleves/bv/mathematiques/les-conditions-minimales-de-similitude-des-triangl-m1266#angle-angle">triangles semblables par AA</a>. Ceci signifie que les deux triangles ont la même forme. On peut alors comparer les côtés semblables.</p>
</body></html>
La relation mathématique existant entre l'objet et l'image dans un sténopé est décrite par l'équation suivante:
|\displaystyle \frac {h_{i}}{h_{o}} =\frac {d_{i}}{d_{o}}|
où
|h_{i}| représente la hauteur de l'image (dans le sténopé)
|h_{o}| représente la hauteur de l'objet
|d_{i}| représente la distance entre l'image et le sténopé
|d_{o}| représente la distance entre l'objet et le sténopé
Les unités de mesure pour les hauteurs doivent être les mêmes, alors que les unités de mesure pour les distances doivent être les mêmes. Toutefois, le choix de l'unité de mesure, que ce soit des centimètres, des mètres, ou toute unité de mesure de longueur, revient à celui ou celle qui résout le problème.
Une personne est placée à une distance de |\small \text {20 m}| d’un arbre. Elle note que l’image de cet arbre a une hauteur de |\small \text {5 cm}| dans une chambre noire qui a une profondeur de |\small \text {10 cm}|. Quelle est la hauteur de cet arbre ?
En remplaçant les variables de l'équation précédente par les données de ce problème converties en mètres, on obtient:
||\begin{align}h_{i} &= 0,05\:\text{m} &d_{i} &= 0,10 \: \text{m}\\
h_{o} &= x&d_{o} &= 20 \: \text{m}\\ \end{align}||
On isole ensuite la variable.
||\begin{align} \frac {h_{i}}{h_{o}} =\frac {d_{i}}{d_{o}} \quad \Rightarrow \quad h_{o} &=
\frac {h_{i} \times d_{o}}{d_{i}} \\ \\
&= \displaystyle \frac{0,05\: \text{m}\times 20 \: \text {m}}{0,10 \: \text {m}}\\ \\
&= 10 \: \text{m} \end{align}||
La hauteur de l’arbre sera donc de |\text {10 m}|.
Un immeuble de |\small \text {20 m}| de hauteur est placé à |\small \text {40 m}| de l’image du sténopé. Si l’image de l’immeuble possède une hauteur de |\small \text {15 cm}|, quelle est la profondeur du sténopé ?
Dans ce problème, ni la distance séparant l’objet du sténopé ni la profondeur du sténopé ne sont mentionnées. Par contre, la distance séparant l’objet et l’image est connue, soit |\small \text {40 m}|.
Ainsi, il est possible d'établir une équation en utilisant une inconnue. Si la distance image-sténopé (soit la profondeur du sténopé) est égale à la variable |x|, alors la distance objet-sténopé peut être déterminée:
|d_{o} + d_{i} = 40 \space \text {m}|
|d_{o} + x = 40 \space \text {m}|
|d_{o} = 40 - x|
En utilisant l'équation du sténopé, il sera donc possible d'isoler la variable représentant la profondeur du sténopé:
||\begin{align} \frac {h_{i}}{h_{o}} =\frac {d_{i}}{d_{o}} \quad\quad \Rightarrow \quad\quad \displaystyle \frac {0,15}{20} &= \frac {x}{40 - x} \\\\
0,15(40 - x) &= 20\cdot x\\\\
6 - 0,15 \cdot x &= 20 \cdot x\\\\
20,15 \cdot x &= 6\\\\
x &= 0,298 \text { m} \end{align}||
La profondeur du sténopé sera donc de |\text {0,298 m}| ou |29,8 \text { cm}|.
La chambre noire est un des nombreux appareils utilisant les propriétés de l'optique. D'autres appareils, utilisant la réflexion et la réfraction, sont expliqués dans les pages ci-dessous: