The pinhole camera, or camera obscura in Latin, is an optical instrument used to collect an image on a flat surface.
A pinhole is a small, narrow hole through which light can enter a light-tight box.
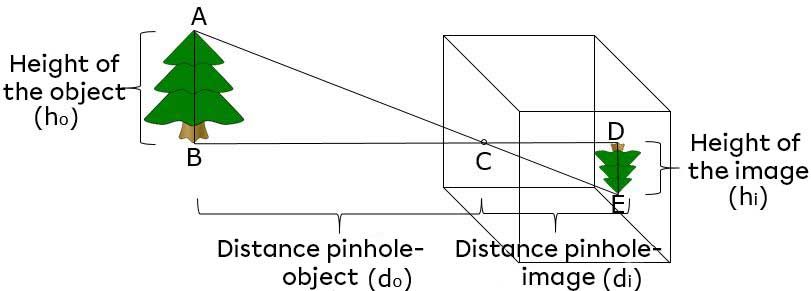
The pinhole camera consists of a closed chamber that is opaque and where a small hole (a pinhole) is drilled so light can enter to form an image. A pinhole uses the optical principle that light travels in a straight line. The following diagram demonstrates how the pinhole works.
In the image above, the light rays coming from the top of the tree are found at the bottom and vice versa. Therefore, the image produced inside a pinhole will always be inverted. In addition, all light rays coming from the object will cross through the pinhole.
The use of a light-tight box can also make it possible to calculate the height of a building or even a distance separating someone from an object using simple mathematical calculations.
Since the triangles ABC and CDE are both right triangles and are opposite by the vertices, they are necessarily triangles similar by AA. It means the two triangles have the same shape. Then, compare the similar sides.
The mathematical relationship between the object and the image in a pinhole is described by the following equation:
|\displaystyle \frac {h_{i}}{h_{o}} =\frac {d_{i}}{d_{o}}|
where
|h_{i}| represents the height of the image (in the pinhole)
|h_{o}| represents the height of the object
|d_{i}| represents the distance between the image and the pinhole
|d_{o}| represents the distance between the object and the pinhole
The unit of measurement for height should be the same, while the units of measurement for distances should be the same. However, the choice of the unit of measurement, whether it is centimetres, metres, or any unit of measurement of length, is up to whoever solves the problem.
A person is placed at a distance of |\small \text {20 m}| from a tree. She notices the image of the tree has a height of |\small \text {5 cm}| in a light-tight box with a depth of |\small \text {10 cm}|. How tall is the tree?
By replacing the variables of the previous equation with the data in the current problem (converted into metres), the following is obtained:
||\begin{align}h_{i} &= 0.05\:\text{m} &d_{i} &= 0.10 \: \text{m}\\
h_{o} &= x&d_{o} &= 20 \: \text{m}\\ \end{align}||
Next, isolate the variable.
||\begin{align} \frac {h_{i}}{h_{o}} =\frac {d_{i}}{d_{o}} \quad \Rightarrow \quad h_{o} &=
\frac {h_{i} \times d_{o}}{d_{i}} \\ \\
&= \displaystyle \frac{0.05\: \text{m}\times 20 \: \text {m}}{0.10 \: \text {m}}\\ \\
&= 10 \: \text{m} \end{align}||
Therefore, the height of the tree will be |\text {10 m}| .
A building that is |\small \text {20 m}| in height is placed |\small \text {40 m}| from the pinhole image. If the image of the building has a height of |\small \text {15 cm}|, how deep is the pinhole?
In this problem, neither the distance between the object and the pinhole nor the depth of the pinhole is mentioned. On the other hand, the distance separating the object and the image is known, i.e., |\small \text {40 m}| .
Thus, it is possible to establish an equation using an unknown. If the image-pinhole distance (i.e., the depth of the pinhole) is equal to the variable |x| , then the object-pinhole distance can be determined:
|d_{o} + d_{i} = 40 \space \text {m}|
|d_{o} + x = 40 \space \text {m}|
|d_{o} = 40 - x|
Using the pinhole equation, it will be possible to isolate the variable representing the depth of the pinhole:
||\begin{align} \frac {h_{i}}{h_{o}} =\frac {d_{i}}{d_{o}} \quad\quad \Rightarrow \quad\quad \displaystyle \frac {0.15}{20} &= \frac {x}{40 - x} \\\\
0.15(40 - x) &= 20\cdot x\\\\
6 - 0.15 \cdot x &= 20 \cdot x\\\\
20.15 \cdot x &= 6\\\\
x &= 0.298 \text { m} \end{align}||
Thus, the depth of the pinhole will be |\text {0.298 m}| or |29.8 \text {cm}|.
The pinhole camera is one of many devices utilizing optical properties. Other devices, which use reflection and refraction, are explained in the following concept sheets: