Le travail |\text{(W)}| est l'effet d'une force appliquée sur un objet qui entraine son déplacement.
Pour qu’un travail ait lieu, il faut que la force appliquée, ou au moins l’une de ses composantes, soit parallèle au déplacement de l’objet.
Si une bille roulant à une vitesse constante n'est pas soumise à des forces de frottement, effectue-t-elle un travail?
Même si cette bille se déplace, on ne peut pas dire qu’elle effectue un travail, puisqu’aucune force n’agit sur elle.
Une personne pousse sur un énorme rocher. Malgré tout, le rocher ne se déplace pas. Effectue-t-elle un travail?
Même si de l'énergie est dépensée par la personne qui pousse sur le rocher, aucun travail n’est transmis au rocher, puisque le rocher ne bouge pas.
Une relation mathématique existe entre le travail, la force et le déplacement de l'objet.
L’équation permettant de calculer le travail est:
|W = F \times \triangle x|
où
|W| représente le travail |\small (\text {J})|
|F| représente la force |\small (\text {N})|
|\triangle x| représente le déplacement de l'objet |\small (\text {m})|
La réponse obtenue est une grandeur scalaire, ce qui signifie que le travail n'a pas d'orientation.
La formule ci-dessus peut être utilisée à chaque fois que la force et le déplacement sont parallèles.
On pousse sur une boîte sur une distance de |\small 12 \: \text {m}|. Si la force de frottement est de |\small 25 \: \text {N}|, quel a été le travail fait par le frottement ?
Dans cette situation, la force de frottement est parallèle au déplacement. Toutefois, elle est en sens opposé, car la force de frottement est une force qui s'oppose au déplacement d'un objet. La force sera donc négative, puisqu'elle est orientée dans le sens contraire au déplacement.
||\begin{align} W = F \times \triangle x
\quad \Rightarrow \quad
W &= - 25 \: \text {N} \times 12 \: \text {m} \\
&= -300 \: \text {J} \end{align}||
Le frottement a donc effectué un travail de |-300 \: \text {J}|. Un travail négatif représente une perte d’énergie. Par conséquent, la force de frottement a soustrait de l’énergie à la boîte.
Lorsque la force et le déplacement ne sont pas parallèles l'une par rapport à l'autre, il faut déterminer la composante de la force qui est parallèle au déplacement.
La formule à utiliser pour déterminer le travail lorsque la force et le déplacement ne sont pas parallèles est:
|W = F \times \cos \theta \times \triangle x|
où
|W| représente le travail |\small (\text {J})|
|F \times \cos \theta| représente la composante de la force parallèle au déplacement |\small (\text {N})|
|\triangle x| représente le déplacement de l'objet |\small (\text {m})|
On applique une force de |\small 150 \: \text {N}| sur un traîneau sur une distance de |\small 200 \: \text {m}| tel qu’illustré sur l’illustration ci-dessous. Quelle quantité de travail a été effectuée sur le traîneau ?
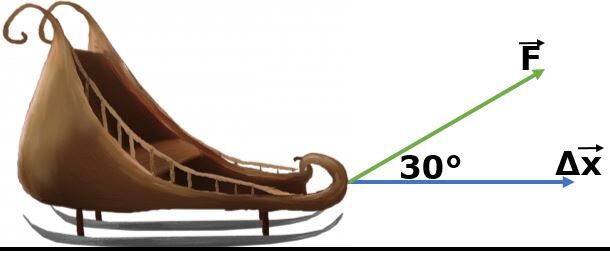
Les informations connues dans ce problème sont les suivantes.
||\begin{align} F &= 150 \: \text {N} &\triangle x &= 200 \: \text {m}\\
\theta &= 30^{\circ} &W &=\: ? \end{align}||
En utilisant la formule précédente, il est possible de déterminer le travail.
||\begin{align} W = F \times \cos \theta \times \triangle x
\quad \Rightarrow \quad
W&= 150 \: \text {N} \times \cos 30^{\circ} \times 200 \: \text {m} \\
&= 25\:981 \: \text {J} \end{align}||
Le travail effectué sur le traîneau est d'environ |25\:981 \: \text {J}|.
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p>Si plusieurs forces sont appliquées sur un objet, il est préférable de trouver la <a href="/fr/eleves/bv/physique/la-force-equilibrante-et-la-force-resultante-de-p1017">force résultante</a> pour ensuite déterminer le travail effectué sur cet objet.</p>
</body></html>
Certains éditeurs utilisent la variable |\triangle S| pour représenter le déplacement. Cette variable est la même que la variable |\triangle x| utilisée dans la formule écrite ci-dessus. Toutefois, l'utilisation de |\triangle x| est privilégiée, car elle représente plus facilement un mouvement à l'horizontale, soit un mouvement suivant l'axe des abscisses.
La puissance mécanique |\small (P)| est le rapport entre la quantité de travail effectué et le temps nécessaire pour faire ce travail.
Plus la quantité de travail transféré par seconde est grande, plus la puissance mécanique sera grande.
La formule suivante doit être utilisée pour calculer la puissance:
|P = \displaystyle \frac {W}{\triangle t}|
où
|P| représente la puissance mécanique |\small (\text {W})|
|W| représente le travail |\small (\text {J})|
|\triangle t| représente la variation de temps |\small (\text {s})|
Un ouvrier réussit à soulever un moteur grâce à un travail de |\small 2 \: 000 \: \text {J}| pendant |\small 5 \: \text {s}|. Quelle puissance l'ouvrier a-t-il fournie ?
||\begin{align} W &= 2 \: 000 \: \text {J} &\triangle t &= 5 \: \text {s}\\
P &= \: ? \end{align}||
||\begin{align} P = \frac {W}{\triangle t}
\quad \Rightarrow \quad
P &= \frac {2\: 000 \: \text {J}}{5 \: \text {s}} \\
&= 400 \: \text {W} \end{align}||
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p>Le travail utile et le travail fourni sont deux concepts utilisés dans le cadre de l’étude des <a href="/fr/eleves/bv/sciences/les-types-de-machines-simples-s1427">machines simples</a>. En fait, l’utilité de la machine simple est de recevoir de l’énergie de l’utilisateur pour la rediriger vers l’objet que l’on veut déplacer. La machine simple a pour but premier de réduire la force à appliquer sur un objet.</p>
</body></html>
Le travail fourni |(W_{f})| se définit comme étant l’énergie que l’utilisateur transmet à la machine simple.
Pour déterminer le travail fourni, on doit multiplier la force motrice fournie par l'utilisateur par le déplacement sur lequel cette force a agi.
L’équation permettant de calculer le travail fourni est:
|W_{f} = F_{m} \times \triangle x_{m}|
où
|W_{f}| représente le travail fourni |\small (\text {J})|
|F_{m}| représente la force motrice |\small (\text {N})|
|\triangle x_{m}| représente le déplacement (moteur) de l'objet |\small \text {(m)}|
Le travail utile |(W_{u})| se définit comme étant l’énergie reçue par l'objet à déplacer.
Pour déterminer le travail utile, on doit multiplier la force résistante nécessaire pour déplacer l'objet par le déplacement que l'objet a fait.
L’équation permettant de calculer le travail utile est:
|W_{u} = F_{r} \times \triangle x_{r}|
où
|W_{u}| représente le travail utile |\small (\text {J})|
|F_{r}| représente la force résistante |\small (\text {N})|
|\triangle x_{r}| représente le déplacement (résistant) de l'objet |\small \text {(m)}|
Le palan (un ensemble de poulies) illustré ci-dessous est utilisé pour soulever un moteur.
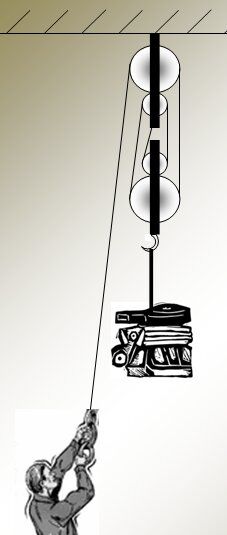
La force avec laquelle l’homme tire est la force motrice |\small (F_{m})|.
La longueur sur laquelle la personne exerce sa force (longueur de corde tirée) est le déplacement moteur |(\small \triangle x_{m})|.
L’énergie que la personne transmet au palan en tirant sur la corde est le travail fourni |\small (W_{f})|.
La force exercée par le palan (représentée par le poids du moteur) est la force résistante |\small (F_{r})|.
La distance sur laquelle le moteur est soulevé par le palan est la distance résistante |\small (\triangle x_{r})|.
L’énergie que le palan donne au moteur en l’élevant dans les airs sera le travail utile |\small (W_{u})|.
<!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN" "http://www.w3.org/TR/REC-html40/loose.dtd">
<html><body><p>En théorie, le travail utile |\small (W_{u})| est toujours égal au travail fourni |\small (W_{f})|.<br>
Par contre, dans la vie de tous les jours, dans tout transfert d’énergie, on doit considérer le frottement. Il y a donc des pertes énergétiques à prévoir. La fiche sur le <a href="/fr/eleves/bv/physique/le-rendement-et-l-avantage-mecanique-p1025">rendement</a> donne les détails nécessaires sur les pertes d’énergie.</p>
</body></html>
Un ouvrier exerce une force de |\small 200 \text { N}| pour soulever le moteur illustré sur le palan ci-dessus. S’il soulève ce moteur de |\small 2,5 \text { m}|, détermine le travail utile et le travail fourni dans cette situation.
Le travail fourni est le travail fait par l’ouvrier. On sait qu’il exerce une force de |\small 200 \text { N}|, mais on ne sait pas combien de mètres de corde il doit tirer pour soulever le moteur de |\small 2,5 \text { m}|. L’avantage mécanique de ce palan est de 4, puisque 4 brins touchent aux poulies mobiles. Par conséquent, l’ouvrier devra forcer sur une distance 4 fois plus grande que |\small 2,5 \text { m}| pour soulever le moteur.
|4 \times 2,5 \text { m} = 10 \text { m}|
Pour déterminer le travail fourni:
||\begin{align} F_r &= 200 \: \text {N} & x_r &= 10 \: \text {m}\\
W &=\: ? \end{align}||
||\begin{align} W_{f} = F_{m} \times \triangle x_{m}
\quad \Rightarrow \quad
W_f&= 200 \: \text {N} \times 10 \: \text {m} \\
&= 2 \:000 \: \text {J} \end{align}||
Comme l’ouvrier tire dans la même direction que la corde se déplace, l’angle entre les deux vecteurs est nécessairement de |\small 0^{\circ}|.
Le travail utile sera le travail effectué par le palan sur le moteur. On sait que le palan soulève le moteur de |\small 2,5 \text { m}|, mais on ne connaît pas la force avec laquelle il le soulève. L’avantage mécanique du palan étant de 4, on sait que le palan exerce une force 4 fois plus grande que l’ouvrier.
|4 \times 200 \text { N} = 800 \text { N}|
Pour déterminer le travail utile:
||\begin{align} F_m &= 800 \: \text {N} & x_m &= 2,5 \: \text {m}\\
W &=\: ? \end{align}||
||\begin{align} W_{u} = F_{r} \times \triangle x_{r}
\quad \Rightarrow \quad
W_u&= 800 \: \text {N} \times 2,5 \: \text {m} \\
&= 2 \:000 \: \text {J} \end{align}||
Comme le palan exerce sa force dans la même direction que le moteur se déplace, l’angle entre les deux vecteurs est nécessairement de |\small 0^{\circ}|. Par ailleurs, on peut constater que le travail fourni et le travail utile sont égaux.
La puissance fournie |(P_{f})| est la rapidité avec laquelle l’énergie est transmise de l’opérateur à une machine simple.
Pour calculer la puissance fournie, la formule à utiliser est la suivante:
|P_{f} = \displaystyle \frac {W_{f}}{\triangle t}|
où
|P_{f}| représente la puissance fournie |\small \text {(W)}|
|W_{f}| représente le travail fourni |\small \text {(J)}|
|\triangle t| représente le temps |\small \text {(s)}|
La puissance utile |(P_{u})| est la rapidité avec laquelle l’énergie est transmise de la machine simple à l’objet à déplacer.
Pour calculer la puissance utile, on utilise la formule suivante:
|P_{u} = \displaystyle \frac {W_{u}}{\triangle t}|
où
|P_{u}| représente la puissance utile |\small \text {(W)}|
|W_{u}| représente le travail utile |\small \text {(J)}|
|\triangle t| représente le temps |\small \text {(s)}|