Work |({W})| is a force acting on an object, causing it to be displaced. This results in a transfer of energy.
There are two essential conditions for this transfer to occur.
- A force must be applied to the object receiving the energy. At least one component of the force must be in the direction of the displacement.
- The object receiving the energy must be moved.
If a ball travelling at a constant speed is not subject to friction forces, is it doing any work?
Even if the ball is displaced, it cannot be said to be doing any work, as there are no forces acting on it.
If a ball travelling at a constant speed is not subject to friction forces, is it doing any work?
Even if the ball is travelling at a distance, it cannot be said to be doing any work, as there are no forces acting on it.
There is a mathematical relationship between work, force and the displacement of the object.
The equation used to calculate work is:
|W = F \times \Delta x|
where
|W| represents the work |\small (\text {J})|
|F| represents the force |\small (\text {N})|
|\Delta x| represents the displacement of the object |\small (\text {m})|
The answer obtained is a scalar quantity, which means that the work has no direction.
The above formula can be used whenever the force and displacement are parallel.
A box is pushed and displaced over |\small 12 \: \text {m}|. If the friction force is|\small 25 \: \text {N}|, what was the work done by the friction ?
In this situation, the friction force is parallel to the displacement. However, it is in the opposite direction, because the friction force is a force that opposes the displacement of an object. The force will therefore be negative, since it is directed in the opposite direction to the displacement.
||\begin{align} W = F \times \Delta x
\quad \Rightarrow \quad
W &= - 25 \: \text {N} \times 12 \: \text {m} \\
&= -300 \: \text {J} \end{align}||
The friction has therefore done a work of |-300 \: \text {J}|. Negative work represents a loss of energy. The friction force has therefore subtracted energy from the box.
When the force and the displacement are not parallel to each other, the component of the force that is parallel to the displacement must be determined.
The formula to use to calculate the work when the force and displacement are not parallel is:
|W = F \times \cos \theta \times \Delta x|
where
|W| represents the work |\small (\text {J})|
|F \times \cos \theta| represents the force component parallel to the displacement |\small (\text {N})|
|\Delta x| represents the displacement of the object |\small (\text {m})|
We apply a force of |\small 150 \: \text {N}| on a sled over a displacement of |\small 200 \: \text {m}| as shown in the illustration below. What amount of work has been involved on the sled ?
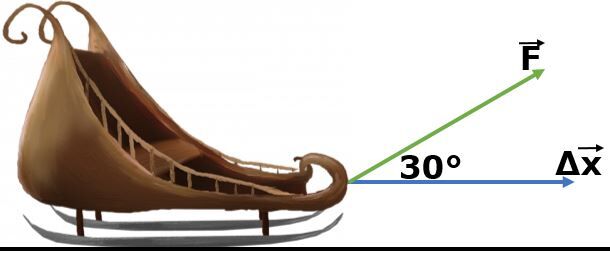
The information provided in this problem is as follows.
||\begin{align} F &= 150 \: \text {N} &\Delta x &= 200 \: \text {m}\\
\theta &= 30^{\circ} &W &=\: ? \end{align}||
Using the previous formula, it is possible to determine the work
||\begin{align} W = F \times \cos \theta \times \Delta x
\quad \Rightarrow \quad
W&= 150 \: \text {N} \times \cos 30^{\circ} \times 200 \: \text {m} \\
&= 25\:981 \: \text {J} \end{align}||
The work done on the sled is approximately |25\:981 \: \text {J}|.
If several forces are applied to an object, it is best to find the resultant force and then determine the work done on the object.
Some editors use the variable |\Delta S| to represent the displacement. This variable is the same as the variable |\Delta x| used in the formula written above. However, the use of |\Delta x| is preferred, as it more easily represents horizontal motion, i.e a motion along the x-axis.
Mechanical power |\small (P)| is the ratio between the amount of work and the time required to do it.
The greater the amount of work transferred per second, the greater the mechanical power.
The following formula should be used to calculate the power:
|P = \displaystyle \frac {W}{\Delta t}|
where
|P| represents the mechanical power |\small (\text {W})|
|W| represents the work |\small (\text {J})|
|\Delta t| represents the variation of time |\small (\text {s})|
A worker manages to lift a motor using the work of |\small 2 \: 000 \: \text {J}| for |\small 5 \: \text {s}|. How much power did the worker supply ?
||\begin{align} W &= 2 \: 000 \: \text {J} &\Delta t &= 5 \: \text {s}\\
P &= \: ? \end{align}||
||\begin{align} P = \frac {W}{\Delta t}
\quad \Rightarrow \quad
P &= \frac {2\: 000 \: \text {J}}{5 \: \text {s}} \\
&= 400 \: \text {W} \end{align}||
Work output and work input are two concepts used in the study of simple machines. In fact, the purpose of the simple machine is to receive energy from the user and redirect it to the object that is to be displaced. The primary purpose of the simple machine is to reduce the force to be applied to an object.
The work input |(W_{in})| is defined as the energy that the user transmits to the simple machine.
To determine the work input, the driving force supplied by the user must be multiplied by the displacement caused by this force.
The equation used to calculate the work intput is:
|W_{in} = F_{d} \times \Delta x_{d}|
where
|W_{in}| represents the work input |\small (\text {J})|
|F_{d}| represents the driving force |\small (\text {N})|
|\Delta x_{d}| represents the displacement by the object |\small \text {(m)}|
The work output |(W_{out})| is defined as the energy received by the object being moved.
To determine the work output, we need to multiply the resistive force required to move the object by the displacement.
The equation used to calculate the work output is:
|W_{out} = F_{r} \times \Delta x_{r}|
where
|W_{out}| represents the work output |\small (\text {J})|
|F_{r}| represents the resistance force |\small (\text {N})|
|\Delta x_{r}| represents the (resisting) displacement of the object |\small \text {(m)}|
The hoist (a set of pulleys) shown below is used to lift a motor.
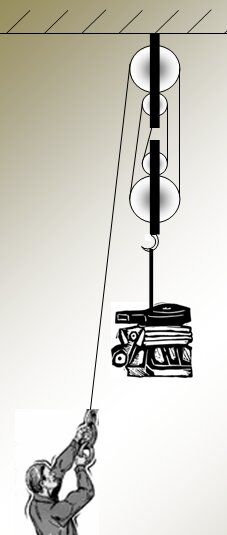
The force with which man pulls is the driving force |\small (F_{d})|.
The displacement by the person exerting the force (length of rope pulled) is the displacement caused by the driving force. |(\small \Delta x_{d})|.
The energy that the person transmits to the hoist by pulling on the rope is the work input. |\small (W_{in})|.
The force exerted by the hoist (represented by the weight of the motor) is the resistive force. |\small (F_{r})|.
The height over which the motor is lifted by the hoist is the resistor distance |\small (\Delta x_{r})|.
The energy that the hoist gives to the motor by lifting it into the air will be the work output. |\small (W_{out})|.
In theory, work output |\small (W_{out})| is always equal to the work input |\small (W_{in})|.On the other hand, in everyday life, in any energy transfer, friction has to be taken into account. So energy losses are to be expected. The sheet on efficiency gives the necessary details on energy losses.
A worker exerts a force of |\small 200 \text { N}| to lift the motor shown on the hoist above. If he lifts this motor |\small 2.5 \text { m}|, determine the work output and the work input in this situation.
The work input is the work done by the worker. We know that he exerts a force of |\small 200 \text { N}|, but we don't know how many metres of rope he has to pull to lift the motor off of |\small 2.5 \text { m}|. The mechanical advantage of this hoist is 4, since 4 strands touch the movable pulleys. As a result, the worker will have to pull over a distance 4 times greater than |\small 2.5 \text { m}| in order to lift the motor.
|4 \times 2.5 \text { m} = 10 \text { m}|
To determine the work input:
||\begin{align} F_r &= 200 \: \text {N} & x_r &= 10 \: \text {m}\\
W_{in} &=\: ? \end{align}||
||\begin{align} W_{in} = F_{d} \times \Delta x_{d}
\quad \Rightarrow \quad
W_{in}&= 200 \: \text {N} \times 10 \: \text {m} \\
&= 2 \:000 \: \text {J} \end{align}||
As the worker pulls in the same direction as the rope, the angle between the two vectors is necessarily |\small 0^{\circ}|.
The work output will be the work done by the hoist on the motor. We know that the hoist lifts the motor by |\small 2.5 \text { m}|, but we don't know the force with which he lifts it. Since the mechanical advantage of the hoist is 4, we know that the hoist exerts a force 4 times greater than the worker.
|4 \times 200 \text { N} = 800 \text { N}|
To determine the work output:
||\begin{align} F_d &= 800 \: \text {N} & x_d &= 2.5 \: \text {m}\\
W_{out} &=\: ? \end{align}||
||\begin{align} W_{out} = F_{r} \times \Delta x_{r}
\quad \Rightarrow \quad
W_{out}&= 800 \: \text {N} \times 2.5 \: \text {m} \\
&= 2 \:000 \: \text {J} \end{align}||
As the hoist exerts its force in the same direction as the displacement of the motor, the angle between the two vectors is necessarily |\small 0^{\circ}|. Moreover, we can see that the work input and the work output are equal.
The power input |(P_{in})| is the speed with which energy is transmitted from the operator to a simple machine.
To calculate the power input, use the following formula:
|P_{in} = \displaystyle \frac {W_{f}}{\Delta t}|
where
|P_{in}| represents the power input |\small \text {(W)}|
|W_{in}| represents the work input |\small \text {(J)}|
|\Delta t| represents the time |\small \text {(s)}|
Power output |(P_{out})| is the speed with which energy is transmitted from the simple machine to the object being displaced.
To calculate the power output, use the following formula:
|P_{out} = \displaystyle \frac {W_{out}}{\Delta t}|
where
|P_{out}| represents the power output |\small \text {(W)}|
|W_{out}| represents the power output |\small \text {(J)}|
|\Delta t| represents the time |\small \text {(s)}|